
Photo by
bokuchibi0501
【インジケーター第9弾】最小二乗法でトレンドラインっぽい線を引くインジ(PineScript付き)
こんな感じです

バックテスト結果

XBTUSD1時間足、2018年1月~で手数料は0.075%
ラインを上抜けしたら買って下抜けしたら売るストラテジーです。
本noteはインジの共有だけでストラテジーは後日のnoteで共有予定です。
TradingViewにdraw Trend Lineで公開しました。
やってること
①まずローカル高値とローカル安値を検出します。
ここでいうローカル高値は左のローソク足を見ても右左のローソク足を見ても自分より高い値がいない場合にローカル高値だと認定します。
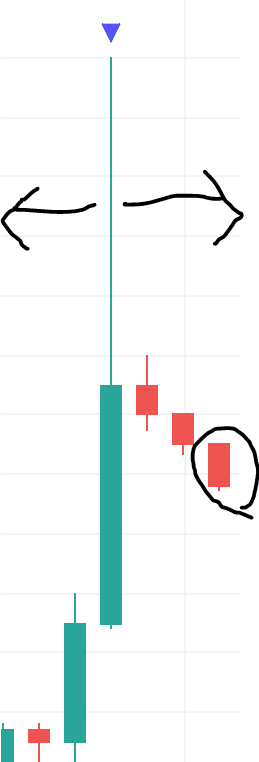
上図は左右ともに3キャンドルを見てローカル高値を決める例です。
右に3キャンドル見る必要があるので黒丸でかこったローソク足が確定してからローカル高値が確定します。

ひきで見るとこんな感じです。
②ローカル高値安値のポイントを使って最小二乗法の計算をします。
最小二乗法をざっくり説明すると複数の点から線引くときに数学的にそれっぽい線を計算する方法でこちらの説明がめちゃくちゃわかりやすいです。
トレンドラインっぽい線を引くためにやってることはまとめると下記です。
①ローカル高値、安値を検出
②ローカル高値、安値をもとに最小二乗法の計算
では結果を見てみます。

ちょっとわかりずらいと思いますので黒丸で囲った線に注目して解説していきます。黒丸部分の線は青丸で囲ったローカル高値から算出した線です。
黒丸の線を過去に伸ばしてみると・・・

こんな感じになります。本当になんとなくですがそれっぽい線が引けているのではないでしょうか。
こんな風にローカル高値が確定するたびにトレンドラインを描画しなおしているので上記のようなギザギザの線のようになるのです。
設定

Length Left:ローカル高値安値を決めるときに何キャンドル左を見るか
Length Right:ローカル高値安値を決めるときに何キャンドル右を見るか
Number Of Points:最小二乗法を計算するときに何点のローカル高値安値を見るか(最小2、最大5)
PineScript
//@version=3
study("draw Trend Line",overlay=true)
len1 = input(8,title="Length Left")
len2 = input(8,title="Length Right")
num = input(2,maxval=5,minval=2,title="Number of Points")
phi = pivothigh(high,len1,len2)
plo = pivotlow(low,len1,len2)
hix1 = n
hiy1 = high
hix2 = n
hiy2 = high
hix3 = n
hiy3 = high
hix4 = n
hiy4 = high
hix5 = n
hiy5 = high
hix1 := phi ? n-len2 : hix1[1]
hiy1 := phi ? high[len2] : hiy1[1]
hix2 := phi ? hix1[1] : hix2[1]
hiy2 := phi ? hiy1[1] : hiy2[1]
hix3 := phi ? hix2[1] : hix3[1]
hiy3 := phi ? hiy2[1] : hiy3[1]
hix4 := phi ? hix3[1] : hix4[1]
hiy4 := phi ? hiy3[1] : hiy4[1]
hix5 := phi ? hix4[1] : hix5[1]
hiy5 := phi ? hiy4[1] : hiy5[1]
x1_hi = hix1
x2_hi = hix2
x3_hi = num >= 3 ? hix3 : 0
x4_hi = num >= 4 ? hix4 : 0
x5_hi = num >= 5 ? hix5 : 0
y1_hi = hiy1
y2_hi = hiy2
y3_hi = num >= 3 ? hiy3 : 0
y4_hi = num >= 4 ? hiy4 : 0
y5_hi = num >= 5 ? hiy5 : 0
lox1 = n
loy1 = high
lox2 = n
loy2 = high
lox3 = n
loy3 = high
lox4 = n
loy4 = high
lox5 = n
loy5 = high
lox1 := plo ? n-len2 : lox1[1]
loy1 := plo ? plo : loy1[1]
lox2 := plo ? lox1[1] : lox2[1]
loy2 := plo ? loy1[1] : loy2[1]
lox3 := plo ? lox2[1] : lox3[1]
loy3 := plo ? loy2[1] : loy3[1]
lox4 := plo ? lox3[1] : lox4[1]
loy4 := plo ? loy3[1] : loy4[1]
lox5 := plo ? lox4[1] : lox5[1]
loy5 := plo ? loy4[1] : loy5[1]
x1_lo = lox1
x2_lo = num >= 2 ? lox2 : 0
x3_lo = num >= 3 ? lox3 : 0
x4_lo = num >= 4 ? lox4 : 0
x5_lo = num >= 5 ? lox5 : 0
y1_lo = loy1
y2_lo = num >= 2 ? loy2 : 0
y3_lo = num >= 3 ? loy3 : 0
y4_lo = num >= 4 ? loy4 : 0
y5_lo = num >= 5 ? loy5 : 0
my_least_squares_method(x1,x2,x3,x4,x5,y1,y2,y3,y4,y5,num) =>
slope = ((x1*y1+x2*y2+x3*y3+x4*y4+x5*y5)/num - (x1+x2+x3+x4+x5)/num*(y1+y2+y3+y4+y5)/num)/((x1*x1+x2*x2+x3*x3+x4*x4+x5*x5)/num - (x1+x2+x3+x4+x5)/num*(x1+x2+x3+x4+x5)/num)
intercept = -1*slope*((x1+x2+x3+x4+x5)/num)+(y1+y2+y3+y4+y5)/num
y = slope*n + intercept
y_hi = my_least_squares_method(x1_hi,x2_hi,x3_hi,x4_hi,x5_hi,y1_hi,y2_hi,y3_hi,y4_hi,y5_hi,num)
y_lo = my_least_squares_method(x1_lo,x2_lo,x3_lo,x4_lo,x5_lo,y1_lo,y2_lo,y3_lo,y4_lo,y5_lo,num)
plot(y_hi,linewidth=2,color=blue)
plot(y_lo,linewidth=2,color=red)
plotshape(phi,style=shape.triangledown,color=blue,offset=-len2)
plotshape(plo,style=shape.triangleup,color=red,offset=-len2,location=location.belowbar)