
大晦日だし弧度法を広めたい
こんばんは、空き (あき) です。
年の瀬に入り、除夜の鐘で108つの煩悩を振り払う大晦日がやってきました。
そしてご存知の通り、108を入れ替えると円の半周の角度である180°ですよね。
そこで、今回は1周が360°という角度の定義に納得がいっていない皆さんのために、弧度法という美しく角度を定義する方法を簡単に10分ほどで紹介したいと思います。
本記事は幅広い層を読者として対象としています。具体的には下記知識を持ち合わせている方が望ましいです。
半径から円周を求めることができる
比が少し分かる
また、弧度法を知っていても、弧度法を機械的に覚えてしまっている方は一定数いるように思われます。
弧度法をイメージして理解することで数学や物理、工学等でなにかと便利です。本記事最後に、弧度法を理解することで簡単に覚えることのできる、よく見る等式をいくつか記載しました。ぜひ読んでいってください。
[1] 円を使って角度を表したい
突然ですが、円の弧の長さで角の大きさを表現できたら嬉しくないですか?
ということで、半径が1の円 (単位円) を考えます(図1)。

ここで弧の長さを角度と考えます。
普段角度を一周(360°)の何等分かを考えて求めていますよね。
半径1の円の円周が、
$$
1 × 2 × \pi = 2\pi
$$
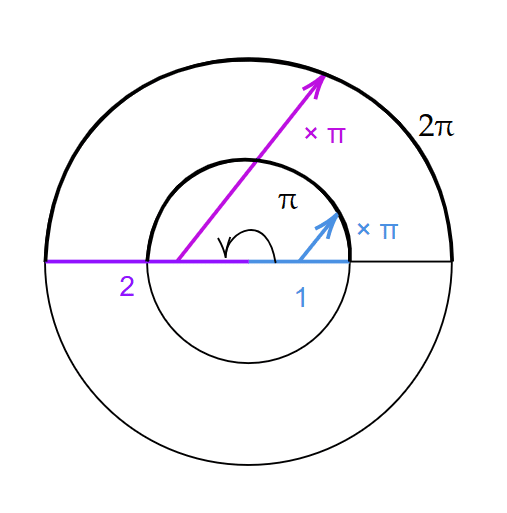
であることを使って、同様に割り算で孤の長さを求めることができます、(図2)。
($${\pi}$$に関しては次章で後述)

左から弧の長さは、2π (1等分)、π (2等分)、π/2 (4等分)
これが弧度法の基本的な考え方です。
1周を360°という、どこから来たかわからない数字よりかは、はるかに納得ができると思います。
しかし、この考え方は少しおかしいです。
なぜなら、同じ角度でも円の大きさによって弧の長さは異なるからです(図3)。

同じ角度だが、内側と外側の円で弧の長さは異なる
仮に、弧の長さをそのまま角度の指標としてしまうと、円の大きさによって弧の長さが変わってしまいます。
同じ角度を統一的に表現できないため、これはかなり不便です。
この問題を解決するために、円の半径と弧の長さの比を考えます。
次の章で、必要な知識である円周率と相似を確認していきます。
[2] 円周率と相似
まず、円周率とはなんでしょうか?
3.1415……と続く謎の数字の列です。これが具体的には何の数字なのかをすぐに説明できますか?
以下に円周率の定義(決まり事)を示します。
円周率(えんしゅうりつ)とは、円の直径に対する円周の長さの比率のことをいい、数学定数の一つである。
簡単に言うと、直径に対して円周が何倍であるかを表す数のことを円周率といいます。
また平面においては、直径に対して円周が3.1415……倍と必ず同じ数になります(図4)。

これは、スマホの画面を使って円を拡大・縮小するとイメージしやすいと思います。直径が2倍、3….倍になったら円周も同じく2倍、3倍….になるので、拡大・縮小の前と後で、円周が直径に対して3.1415….倍であるということは変わりません。
このように、拡大・縮小しても、対応する長さの比が一定である図形を互いに相似であるといいます。すべての円はその性質を持ち、相似な図形です。
あと、円周率は無限に続くことが知られており、書くのがとっても大変であるので代用として$${\pi}$$(パイ)という文字がよく使用されます。本記事もこれにならい円周率を$${\pi}$$と表記します。
[3] 半径と弧の比率を角度とする
前章で復習した相似を用いて、「弧の長さを角の大きさとすると、同じ角度でも円によって違う長さになるため不便である」という問題を解決します。
まず、図5のような角度は同じだけれど半径・弧の長さは異なる円を考えます。
「全ての円は相似である」ということから、これらの円において半径に対して、弧の長さの比は必ず同じです。
言い換えると、角度が同じであるならば、どんな円でも半径に対する、(その角度の)弧の倍率は同じです。
これとってもすごくないですか!?!?
なぜなら、半径に対する弧の比を角度とすることで、先ほど示した問題を見事解決することができるからです。
これが弧度法です。半径に対する弧の比を角度とするんですね。
よって下の (1) 式で角度(半径と弧の比)を求めることができます。単位は $${rad}$$ (ラジアン)です。
$$
角度(rad) = \frac{弧の長さ}{半径} … (1)
$$
そして、この式を眺めると他のことが分かります。
ここで、半径について少し考えてみましょう。半径1の円を基準としたとき、円の半径はそのまま拡大率(何倍に拡大されたか)として解釈できます。
例えば、半径2の円は半径1の円に対して2倍に拡大されており、2は半径の長さです。

もしくは、
半径2の円の弧 ÷ 2 = 半径1の円の弧
ということは、(1)式は(2)式のように書き換えることができます。
$$
角度(rad) = \frac{弧の長さ}{円の拡大率} … (2)
$$
(2) 式の右辺 (右側の式) は、孤の長さを拡大率で割っています。つまり、円を半径1の円に拡大・縮小したときの弧の長さを求めていると考えることができます。
よって、半径1であるときときの弧の長さがその角度(ラジアン)を直接表すということが言えます。
まとめると、角度 (ラジアン) に関して
弧の長さ ÷ 半径
半径1の円 (単位円) における弧の長さ
という2つの定義ができます。
どちらも正しいです。好きなほうを使ってください。
角度 (ラジアン) の具体例を示してこの章を終えます。
1周は$${2\pi [rad]}$$であるため、360°の場合と同じく求めたい角度が何等分であるかを考えるとわかりやすいです。
例えば、同様に半直線は1周の等分、直角は1周を4等分しているので、それぞれ、
$${2\pi [rad]}$$ ÷ 2 = $${\pi [rad]}$$
$${2\pi [rad]}$$ ÷ 4 = $${\pi / 2 [rad]}$$
で求めることができます(図6)。

また、図7の角度 (ラジアン) は1周の6等分がいくつあるかを考えます。
$${2\pi [rad]}$$ ÷ 6= $${\pi / 3 [rad]}$$
$${2\pi [rad]}$$ ÷ 6 × 2 = $${2\pi / 3 [rad]}$$
で求めることができます。

[4] 最後に
以上が弧度法の解説です。
ここまでお付き合い頂きありがとうございました。
お疲れ様でした!!
ここまで理解した貴方は、この先の学問を少し有利に進めるかもしません。将来に関係ないわ、という方でも日常で角度は用いますので、是非弧度法を導入していただければと思います。
弧度法は、弧の長さを用いて自然に角度を定義できるという点において、とてもユニークな考えです。これすごい発想ですよね。
また、1周を360°とするという考え方を度数法といい、これは昔の暦において1年が360日ということに由来しているそうです。
360という数は、1年の日数に由来すると言われる。ペルシア暦のような初期の暦法では、1年は360日とされていた。1周を360度とすることで、星が北極星を中心とする円を1日1度回ることになり、星を観測する際に便利である。
星が出てくるので、これはこれで心が躍りますね。
また、私はnoteで弧度法の良さを布教したいという思いをくすぶらせてこの1年を生活していました。
執筆を終えた今、180個の煩悩を振り払って無事に年を越すことができそうです。
最後になりますが、私はあくまで弧度法を愛する一介の学生です。従って、誤りや分かりにくい箇所等があるかもしれません。その際はコメント等で指摘してくださると大変助かります。優しいコメントだとさらに喜びます。応援コメントだと卒倒します。
質問は随時受け付けています!!
(付録) 便利な等式集
角度( θ ) と正弦比( sinθ ) 間の近似式を直感的に理解する
$${\theta [rad]}$$が十分小さいとき( | θ | ≪ 1 )において、
$$
sin{\theta} \approx {\theta} … (3)
$$
この近似式、物理でとてもよく目にしますね。私は最近、単振り子の周期測定とヤングの干渉実験で用いました。
これを厳密に導出しようとすると$${sin\theta}$$のマクローリン展開の2次以降の項を落とすことで求めれるのですが、いまいち直感的ではないです。
しかし弧度法を理解すると、図8のように考えることができます。

単位円において、
孤の長さ = 角度
三角形の高さ = $${sin\theta}$$
であることに注意してください。
$${sin\theta}$$と$${\theta}$$がほぼ同じ長さに見えますよね?(証明終了)
扇形の面積
半径$${r}$$、中心角$${\theta}$$の扇形の面積を$${S}$$とおくと、弧の長さは(1)式より、$${r\theta}$$である(弧は角度の半径倍)。
これをな、こうして、こうじゃ (図9)。

図は結構適当
極限の考え方を用います。小学生の頃に扇形の紙を切って長方形を作りませんでしたか?それです。
$$
S = \frac{1}{2}r^2\theta … (4)
$$
その他の利便性
下記サイトの、「弧度法を使うメリット」、「弧度法だと美しい」という項においてとても分かりやすく解説されています。ぜひご覧になってください。
