『ボーアとアインシュタインに量子を読む』第１章

1.1 熱輻射をめぐって

1.1.1 熱輻射研究前史

熱輻射の研究はKirchhoffの「黒体」に始まる。
黒体は電磁波を反射しないので、表面から発する熱輻射だけが見える。
Kirchhoffは物体の輻射能と吸収係数の比が振動数νと温度Tだけの函数であることを示した。

特に黒体の場合、輻射能のスペクトル分布は、波長λと温度Tだけで決まる不変的な函数ρ(λ,T)であることになる。

スペクトル分布とは、波長ごとの度数分布である。度数ρは単位体積あたりのエネルギー(エネルギー密度)でカウントする。
黒体輻射は空洞の穴で実現される。これが空洞輻射である。ということもKirchhoffは示した。

この辺りの話は、田崎統計力学Iの7-1に詳しい。
スペクトル分布が温度とともにどのように変化するかということが19c末、主にベルリンとウィーンで研究されたが、古典物理学では導出できない。

Planckの研究以前、Wienは
ρ=ν^3 f(ν/T)
を導いた。これをνで微分すれば、スペクトル分布函数ρの挙動が分かる。

第1項は正だからほっておく。第2項が最大値を取るときのξをξmaxとする。
ξで最大値をとるという理由がまだよく分からないが、進む。
ξmax=νmax/Tだから、νmaxやTがどんな値をとっても、ξmax=const.に束縛されて変化する。

λmax=(c/ξmax)/T=(const.)/T
ある温度T1で強度ρが最大となるλ=λmax1がわかれば、他の温度T2で強度が最大となるλ=λmax2がわかる。これが変位則という名称の由来である。
これは熱力学だけからの導出なので厳密に正しく、ρのすなわちfの正確な形の決定が課題となる。
後のプランクの法則からグラフを描けば次のようになる。p13図1-2には江沢先生の書からの正確なグラフがあるがタネを知らずに読む方が歴史的経緯が分かりやすいかも知れない。なぜなら、fの函数形はまだ明らかにされていないからだ。

結局、熱力学から導出されたWienの法則(1.1)は厳密に正しく出発点になるということ、そして変位則から、函数形fはよく分からんけど、ある温度Tの黒体熱輻射のスペクトル分布のうち最もエネルギーの大きい(度数を多く含む)波長が求められるということなのである。例えば体温が37℃の体なら、波長10,000nm近辺をピークとする遠赤外線が熱輻射されている。

1.1.2 planckの熱輻射公式

次の有名な公式の導出

1900-1901 Planckの論文
Annalen der Physik
C1:『物理学古典論文叢書』東海大学出版会
叢書 (そうしょ) とは出版形式の一つ。 一度世に出た単行の書物を集め，一定の書式に整え，総名を冠し，ひとまとめの書物として再出版したものをいう。
Planckの元々の意図は、熱力学第二法則を電気力学的に基礎づけることであり、熱輻射はメインではなくその題材であった。後にエントロピーの記述がある。
完全反射の壁では熱平衡に達しないので、壁に共鳴子があるとする。

問題を輻射そのものから、輻射と共鳴子に置き換えた。
温度Tでの、ρとηの関係を導いた。
ηは共鳴子の平均エネルギー

電気双極子としての共鳴子の運動方程式から(1.6)を得る。

電気双極子の放射するエネルギーはLarmorの公式により与えられる。
L&L小教程力学・場の理論p359が本文のノーテーションに近い。

Larmorの公式については太田『電磁気学の基礎２』p427,p433にもある。
(L&Lはスッキリ書かれてあって読みやすい。一方太田は歴史的な記述があり興味深い。注釈9にある太田『電磁気学』2000丸善は書店に無いようなので、改訂版『電磁気学の基礎２』の参考箇所を付した。こんなふうに、山本先生は名著の参考箇所を丁寧に示してくださるので大変うれしい。)
(1.6)と次の式からp7最後の式を得る。
p8初めのαの式は易しい。

4行目「したがって」の次式は1行目のv.=iαvから考える。αの大きさがωとなることに注意すれば、二乗平均の比率がω^2となることがすぐ分かる。

p7の最後の式にこの結果を使えば、
γ≪ωが導出できるということになっている。

なぜγ≪ω^2ならγ≪ωなのか分からんが、進む。
(1.7)までは次のnote

この微分方程式(1.7)は空洞のエネルギー減少は、減衰係数γに比例することを意味している。

(1.8)からスタートする。
Fourier変換
E(t)→E(Ω)   r(t)→r(Ω)
によって(1.8)を解く。
フーリエ変換は
E(Ω)=(1/2π)∫(-π→π)E(t)exp(-iΩt)dt
で定義される。
E(t)を、exp(-int)を基底として成分anの級数で表すのがフーリエ級数展開
E(t)=Σan exp(-int)
である。これは例えばexp(-i1t)という波動モードがa1個、exp(-i2t)という波動モードがa2個、nをたくさん合成すればE(t)が再現される(収束する)ということである。anはexp(-int)というモードたちの度数たちを表している。ということは、波動モードをnとラベルして、度数anたちを数えれば、ステレオのイコライザーをイメージできる。これをスペクトル分解という。
nは自然数だがこれを連続した実数Ωとすれば、そのモードΩがどのくらいあるのか、すなわちE(Ω)を求めるのがフーリエ変換である。
直感的には函数のフーリエ係数(度数)を連続したラベルで求めるのがフーリエ変換に他ならない。ここら辺の理論は村上『なるほどフーリエ解析』海鳴り社が大変分かりやすい。
フーリエ解析の書は物理Gachtにとっては大事だか、フーリエ変換の理論まで学ぶ前に力尽きることもあるのではないだろうか。まずは村上フーリエ解析を1週間以内に一気に読んで、次に江沢先生の『理工学者が書いた数学の本 フーリエ解析』をおススメする。江沢先生の本は、ベクトル空間とフーリエ解析のつながりなど、深く学習することができる。早めに複素フーリエ解析に突入して見通しが良いのが特徴。ただ、計算を手で追うのが大変なのでじっくり取り組む時間が必要。大変面白い本です。
村上フーリエ解析の他、キーポイントシリーズや、大石先生のも良いと思う。

振動子が電場からなされる仕事率はp8の最後の式を定義として、これにParsevalの公式を使う。Fourier変換前後で函数の内積(eE|v)が変化しないというののがParsevalの公式である。
これから前述の仕事率を計算していく。

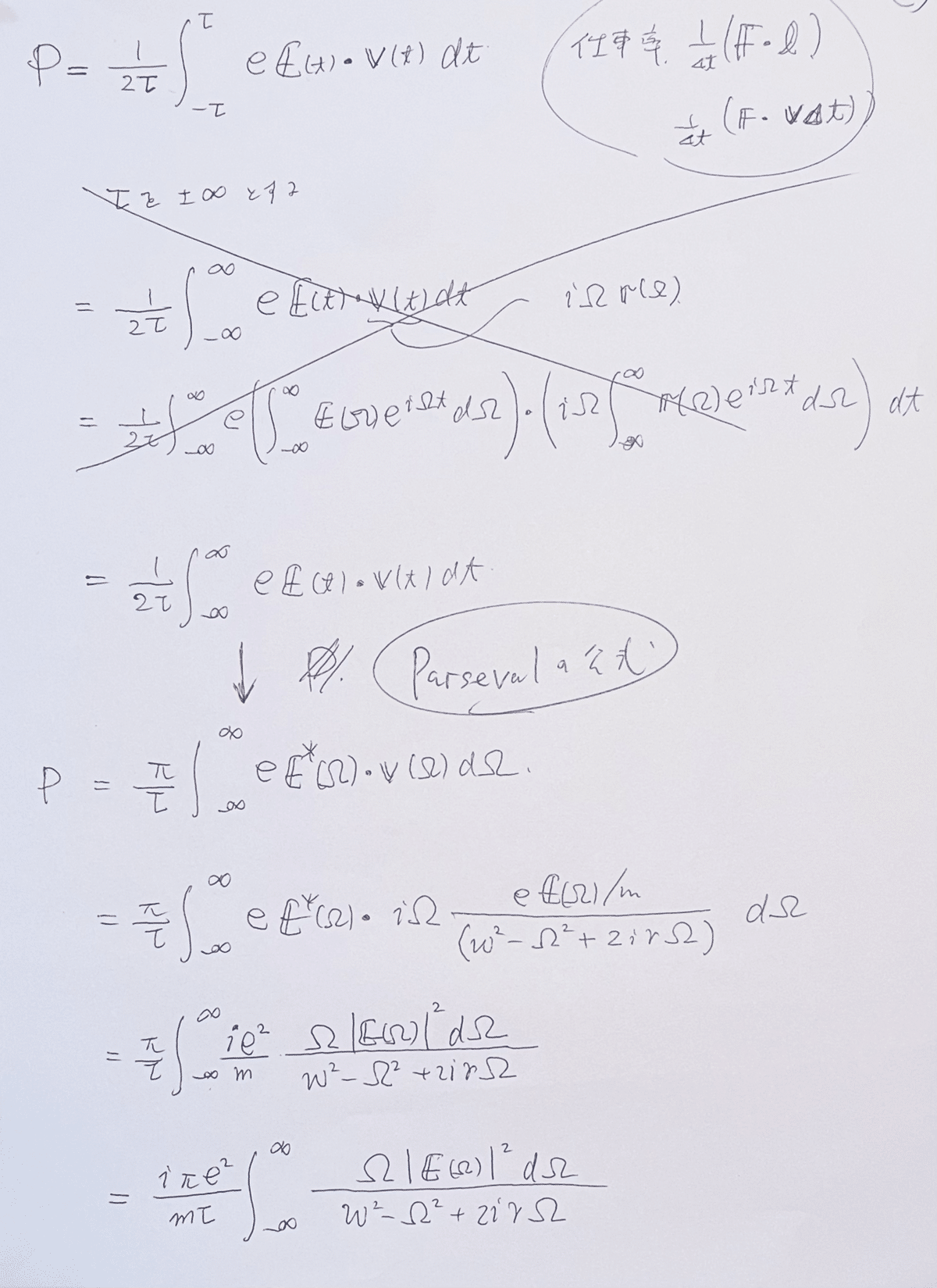
積分は次のように展開する。

p9真ん中へん、輻射のエネルギー密度から。U=1/8π(E^2+H^2)の公式は例えばL&L p275にあり。

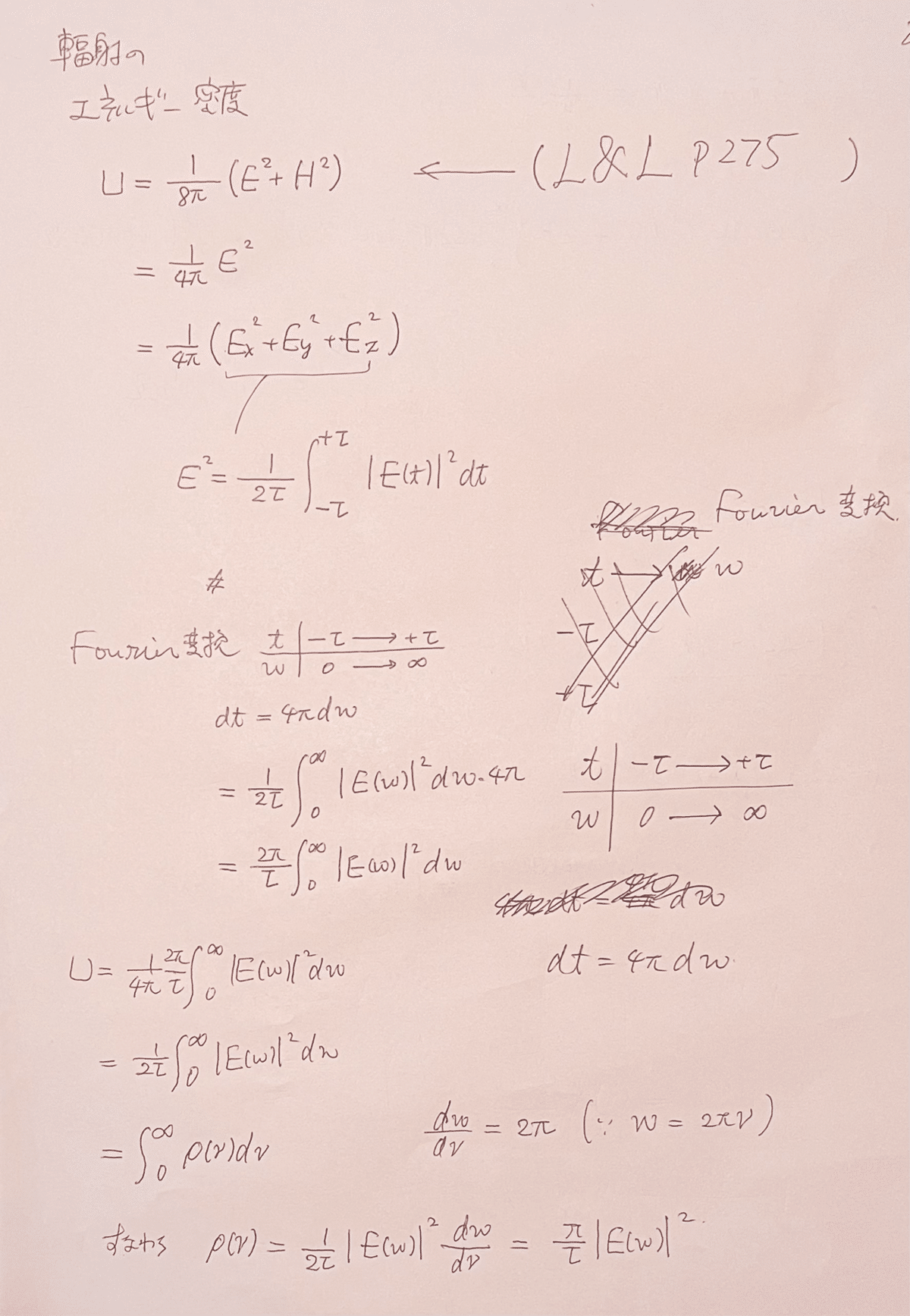
こうして、次のようにして、Planckの平衡条件(1.11)を得る。

Planckは、冒頭に書いてあるように熱力学第二法則を電気力学で基礎づけることを目的としていたので(かは書いていないが、)(1.13)のエントロピーを定義している。Wienの分布則の修正を取り入れながら、ついに(1.19)を導出した。
図1.2の各曲線の極大値が「変位」していることが分かる。

1.2 量子化のはじまり

RJとWの公式、をds/dη=1/Tそれぞれに代入、エントロピーの２回微分の公式たち(1.26-1)を得る。
hνとkTの大小によって(1.26-1)に漸近するように一つの式を作ったのが(1.26)である。
hν≫kT(高振動数)ならhν≫ηでW
hν≪kT(低振動数)ならhν≪ηでRJ
プランクの公式(1.16)はローレンツに認められたにもよらず、プランクは，満足せず、物理的な意味を考察した。
プランクはエントロピーを基軸にしていたので、(1.26)を積分してエントロピーの表式を得、その成因を明らかにすることに努めた。(1.26)の積分は

となり、(1.27)っぽく計算できたが、積分定数処理が分からん。
ここからは微視的状態数を計算して、ボルツマンの式から、エントロピーを再現する。
振動数νiのNi個の共鳴子にPi個のエネルギー要素εi=Ei/Piを分配する。振動数νiの共鳴子の平均エネルギーは
ηi=Ei/Ni=εPi/Ni
Pi個のエネルギー要素εiをNi個の共鳴子に分配する仕方の数は(1.28)で、近似を使い、全部の微視的状態数は積の法則より、(1.29)を得る。

と、このように、エネルギーが連続量ではなく、εiと量子化して、状態数を数えあげられるようになったのがミソだが、プランクにとっては、これは量子ではなく、計算の便法と見るべきだろう。つまり、プランクがエネルギー量子hνを見つけたという見方をしてはいけないと書いてある。この辺の歴史的事実？は読んでいて大変面白い。
とにかく、(1.29)とボルツマンの式から、(1.27)が再現された。(1.27)がエントロピーや便法的エネルギー量子によって意味づけられた。
全エネルギーは一定という拘束条件で、Wを最大にする配分の仕方が熱平衡状態を与える。これには、ラグランジュの未定乗数法が使える。詳しくはキーポイント多変数。そして改めてプランクの公式(1.30)を得る。
とにかくプランクにとっては、hν単位のエネルギーやり取り仮定はエントロピー計算をするための便法であって、量子化されているといったわけでは決してない。
ここからデバイの話がつづく。
ラーモアの公式は古典電気力学で輻射は連続的な電磁場を前提にしているが受け渡しの時だけ量子化するのは変だ。
デバイは共鳴子を用いず、輻射の各モードをhνと量子化を試みる。しかこれもモード数を求める際古典電磁波理論に依拠した。
プランクはhやkを計算し、アボガドロ定数や電気素量を与えた。
hは物理系の大小に対する絶対的な尺度を与える。世界像から人間的条件への言及を排除するプランクの思想にのっとったものであった。