
山本解析力学 §3 変分原理
§3.1
§3.1.1
ダランベールの原理2.1.8式からラグランジュ方程式の導出をおさらいする。

最後でイコールゼロ。
このラグランジュ方程式の左辺を積分する。p165の1行目から2行目は次のように部分積分する。

両端は動かさないから、δLの時間積分はゼロとなる。
系が実際にとる運動経路にそったラグランジアンの積分は、端点を固定して、途中経路を仮想的に無限小だけ変化させても、その値を変えない。例えば石ころを投げて放物運動させる。この場合の配位空間は3次元と同じ。放物線から少しでもずれると、変分がゼロでなくなる。この辺の話はファインマン講義の3巻参照。
次の概念を説明せよ。
作用積分
変分
停留曲線 極値曲線
ハミルトンの原理
正確には、作用積分は配位空間上の曲線をいろいろ変えて積分してみるわけだから、曲線によって値を変える。y=x^2とy=x^4の0~1の積分値を比較するようなもので、これを汎函数という。作用積分は経路cLの汎函数だ。作用積分を局所座標で表示することもできる。現実に辿る経路cLは停留曲線で与えられる。
最後に注意として、ラグランジアンを状態空間上の関数とみるとき、q.は接空間上の任意のベクトルというわけではなく、cLの接ベクトルに限定されるから、q.はqからから決まる。よって、作用積分はcL=qだけの汎函数なのである。

§3.1.2
ハミルトンの原理で表現した力学は、系の時間的発展の全体を同時的に捉えることが特徴である。
六本松から城南線に沿って博多駅に行くことを考えよう。

これは2次元の配位空間である。これではどの時刻にどこにいたかが分からないが、時間軸を付け足すと

となる。この場合は薬院で休憩していたことがグローバルに捉えられる。
ハミルトンの原理は系の時間的発展を、上のように一目で同時的に捉えるのが特徴だから、変分計算は拡大配位空間で行う方が自然なのだ。
したがって、作用積分はN×Rの局所座標系q~,q’~を用いて3.1.6のように表す。
§3.1.3
ただし、拡大配位空間に伴う拡大状態空間の次元は2n+2ではなく、2n+1である。物理的にはそうなるが、数学的にはオイラーの定理を用いて3.1.8が導出でき、これが1つの拘束条件となっているのだろう。
オイラーの定理は笠原微分積分学p160を参考に理解した。

余談ですが、
山本解析力学の数学については、初等的な解析学と線形代数学のみを前提としているが、具体的にはどんな教科書を使えば良いのだろうか。高木の解析概論あたりか、杉浦解析入門か。いずれにしても数学色が強くて通読する気になれぬ。私はいちおう笠原や齋藤の微分積分学を多用している。が、もう少し理工寄りの、しかもヤコビアンや陰関数定理に詳しい解析学書はないものだろうか。理工寄りのなどと考えているうちは数理物理専攻などとは言えんのかも知れぬ。
あぁ、数学が足りぬ。いちど2、3年使って数学やりなおそうかな〜。いや多変数の微分法だけでもやり直しとくか。
§3.1.4
いきなり基本1形式の定義から始まるが、第1項は2.2.5からおそらく一般化運動量のようなものだろう。いや、3.1.12に答があった。間違いなく一般化運動量piであった。
結論3.1.14を先にながめる。拡大配位空間の基本1形式はΘL=θL-HLdt
で表される。もちろん多様体上の幾何学的対象、微分形式であるから共変性を持つ物理量である。θは2.3.5で定義したθ=pdqだから、Θはこれにp0dq0を足した形で、確かに基本1形式も拡大されている。すなわち、拡大配位空間における一般化座標q0=tに共役な一般化運動量p0はハミルトニアンなのだ。
そして拡大配位空間上で作用積分が示される。ΘLを曲線c ~Lに沿って線積分すれば、作用積分となる。線積分はp93で学んだ。1形式と曲線の接ベクトル場の双対内積をとり、これを積分したものである。
ここで拡大配位空間のハミルトンの原理が表される。拡大配位空間N×R上の現実の経路はI~の停留曲線である。
静力学の釣り合いはポテンシャルの停留値、動力学の現実経路は作用積分の停留値から決定される。現実の動きを釣り合いの一種だとみなすのは面白い。釣り合いでも現実の経路でも自然な状態というのは、何かの量が停留しているのだ。
3.1.13までの計算 大変苦労したよ

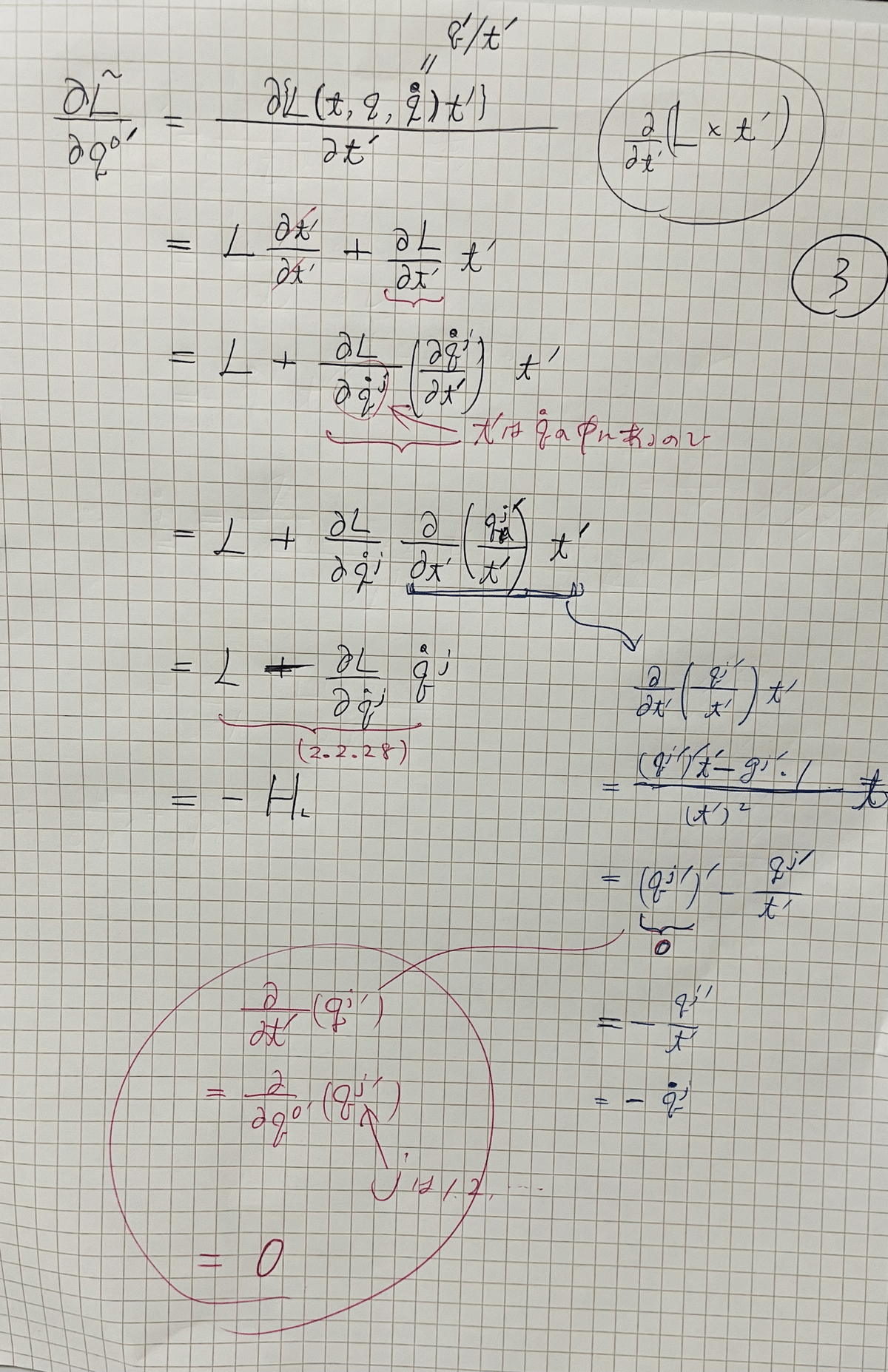

物理っちゅうのはウンウン唸って考えて、面倒がらずに手を動 かして計算せな、自分のものにならんのよ。
Θの点変換による共変性
Θの線積分による作用積分
§3.1.5
端点固定しない変分。固定しないのか〜難しそうだな〜と思う反面、確かに途中のバタバタする部分をしっかり考えて、変分にたいする一般的な知見を得ることができそうだ。難しそうなので、先に3.1.32を眺めたり、書写したり、意味を考えたりして、モチベーションを高めてみる。
記号が面倒なので、 チルダやLなどは省略する。
cをc+Δcにわずかに動かす。ストークスの定理を使うなどして、曲線cの作用積分ΔI[c]は2種類の積分を求めればよいことになる3.1.19式。
はじめの積分、すなわち端点移動に伴う基本1形式の線積分は、c上の点からの任意の動き(場)で表す。これをd/dλとする。
拡大局所座標qiは、パラメタτ、ηで表したので、その全変分Δqiはηとτに関わるはずである。
結局、任意の動き場はd/dλ=3.1.22aと表され、3.1.22bのように全変分=δ変分+τ変分で表される。なお、この式の双対内積はqiの変化率を表すことが分かる。

結局、3.1.19の端点積分は、lの接ベクトルvλを使えば、3.1.24のように表せる。この積分は全変分のQでの変化ということになり結局、端点積分の計算結果は、微分形式と局所座標表示で3.1.26となる。
一方、3.1.19の面積分から3.1.31を得る。途中で、1.6.63の面積分の定義を使う。いろいろ抽象的な計算を使うので大変だがやりがいがある。2形式の微分形式計算や公式化のトレーニングと思って頑張った。

完成した3.1.32をもう一度眺めてみよう。なんとも美しい式ではないの。特に2行目の微分形式が意味深で、イメージ力を高めてくれる。

2行目1項の双対内積はλ方向への変化率の関数を表している。τが引数で、端点を固定するなら当然ゼロになる。大概の教科書にはこの部分がない。山本解析ならではじゃないの?
2行目2項の2形式の双対内積?あるいは実数値函数は、局所座標ではラグランジュ方程式の左辺(0ではない)を表す。< >にδ変分δηを掛けていることから、< >は何を表すのだろうか?1.6.3節によれば、dΘはなんらかのテンソル場らしく、1.6.4節や後章を参考にして考えてみよう。

§3.1.6
ε[L]=0ならばΔI=0
補題からΔIならばε[L]=0で作用積分の停留曲線がラグランジュ方程式を与える。
作用積分の停留曲線がラグランジュ方程式の解曲線である。したがって、ハミルトンの原理は力学原理の表現のひとつである。ただまえに書いてあったように、ハミルトンの原理による軌道の決定は大局的かつ一挙的、global&allatonceである。これでやっと拡大配位空間のラグランジュ方程式表現の準備ができた。
§3.1.7
ラグランジュ方程式の幾何学的表現は3.1.35で与えられる。これが局所座標表示の、いつものラグランジュ方程式であることを示す。



p178の初めの式から3.1.41が導かれ、Lがtを陽に含まないならHが第一積分(保存量)になることが分かる。
§3.2
§3.2.1 ワイスの原理
一般化座標を時間の函数として求める(積分する)ほか、系の物理的性質を知る手立てがある。
ラグランジュ方程式を経由せず、系の興味ある特徴を直接に読み取る。それは保存則である。
現実経路に沿って計算した3.1.32は端点からの寄与のみになる。
cがラグランジュ方程式の解曲線であるための必要十分条件はcにそった作用積分の変分が端点からの寄与のみから与えられる。
これをワイスの原理という。この変分はラグランジュ方程式に他ならない。
§3.2.2 ネーターの定理の拡張
ラグランジアンLに、Dを作用させる。
D:=∂qi fi+∂q.i f.i
要はDと状態空間上のベクトル場だ(2.2.15)
方々への一般的な無限小変換
Q=q+εμfμに対して、D[L]=dΛ/dtとなるΛが存在する時、ネーターカレントJは保存される。
無限小変換にたいする普遍性すなわち対称性のぶんだけ、これを系が許容する写像というが、そのぶんだけ第1積分が存在する。
作用積分の変分はεΛだが、ワイスの原理よりこれはεpfに等しく、
pf=Λ
pf-Λは端点tで等しくなければならない。すなわち保存される
このpf-Λがネーターカレントである。
ネーターカレントはモーメント函数を一般化したものである。方々への無限小変換に基づくものだから。
ゲージ変換に似た考えが出てきている気がするので、今度つぎの復習をする。
§2.2.5
§2.2.3
§3.2.2
この節が今までで一番難しい気がするのは気のせいだろうか。100回読んで慣れ突破するが、そろそろ知能の限界か。否❗️とにかく頑張る。
誰か一緒に勉強しませんか〜
§3.3
§3.3.1 保存系と作用
ラグランジアンが時間tを陽に含まないときはハミルトニアンが第1積分であって
H=Eとなる。(3.3.1)の三番目のイコールは(3.1.13)と同じものである。
保存系はエネルギー保存則の成り立つ系である。
tを循環座標としたラウシアンの方法が使えるが、この簡約によってハミルトンの原理に新しい表現が与えられるとはどういうことだろうか?
tを循環座標として簡略化したラグランジアンRの作用積分を作用と呼ぶ。
作用積分が単に作用と呼ばれたときはエネルギー保存則(保存系)が前提にあることに注意。
作用Aは基本1形式を使って(3.3.6)のように表すこともできる。ほほう、ということはθ=pdqの積分になるのだな。これが「新しい表現」というやつか。
q0‘をq、q・、tを使って明示的に表す(閉じた形)と表せない(閉じていない形)で別々に取り扱うというのはどういうことだろうか。あまり気にせずに次に進んでみることにする。
ちなみにラウシアンはL&L力学の§41にさらさらさら〜っと書いてありもす。
§3.3.2 最小作用の原理
とりあえず、保存系と作用の意味はわかったのでとりあえず良しとする。
q0‘が明示的でない→(3.3.1)は付加的な拘束条件である。の意味がさっぱり分からない。とりあえず進める
拡大空間ではtを消した。保存系ではtが消えている。ということは、保存系では拡大配位空間におけるおけるハミルトンの原理と相似(初めてみる表現だ)の変分原理が成り立つ。
p197の表が分かりやすいですね。
何を求めたいかというと、作用Aの変分ΔAを求めたいのである。
3.3.7から3.3.9へ辿り着く(このとき変分法の基本公式3.1.32を使う。がんばって3.1.32もとめておいて良かったな!)。
p197「しかし、」からだんだん難しくなってきたぞ。「途中経路を変化させれば端点通過時刻も変わる」というところがキーポイントとなりそうだ。初期位置と初速度を固定した放物運動で終端の時刻をtとするとき、放物運動からずらした場合の終端時刻は放物運動のtとは異なる。
つまり変分はつねにエネルギー保存を満たすようにとるので、経路の変化にともなって経路上の移動速度も変わり、そのため経路上の点を通過する時刻が現実の経路にそったものと違ってくるのである。
同様の考察が小出解析力学のp72-p75にあったので転載する。

原島力学Ⅱのp34にもあります。モーペルチュイ自身の考察は山本先生の重力と力学的世界下p130あたりにあります。
「この困難は〜細工すれば回避できる」3.1.41 dH/dt=εi[L]qi-∂L/∂tから、
第2項が0である。一方3.3.9のδq=Δq-qΔtだから、Δtの項が消える!!しゅげぇぇ!エレガンス!
ここの部分、初読では意味がさっぱりわからんかったが、小出などを読んで具体的イメージを作って読めばすーっと通せると思います。具体的なイメージって大事だな〜。
結局3.3.11の秘宝を得る。
保存系におけるワイスの原理は3.3.11の第1項。系が現実にとる経路の始点から任意の点までのその経路にそって積分した作用は端点のみの函数となる。これをハミルトンの特性函数wという。主関数3.2.2との関係は
S=W-Etとなる。
以上が3.3.2のようには閉じていない形の議論である。
§3.3.3 ヤコビの原理
エネルギー保存系のつづき。系の運動が,Q1,Q2を通るならばその途中で系がとる現実の経路は,積分
A=∫[Q1,Q2]√(2T mij dqi dqj)
停留曲線ので与えられる。
2T×(計量テンソル)の平方根を積分している。2T mijはヤコビ計量gijという。
作用Aまでは3.3.15から丁寧に辿ればたどり着ける。
3.3.17でi=0からのΣ記号が解除され,Einsteinの規則に従う。
§3.3.4 測地線の方程式
力が「空間の計量」を決め,物体はその「計量空間」内をつねに慣性運動する,というのがEinstein流の見方である。計量や計量空間とは何か。
力の効果を座標軸の曲がりで表すことを,力の場を計量に「くりこむ」とよんでいる。
