
山本解析力学§1 数学的準備(随時更新)
§1.1 運動方程式
§1.1.1 ニュートン力学
疑問
力自体の法則は、力学の外にある場の古典論で取り扱われるべきもの。
力学の課題の2方向性は、力学の原理である運動方程式の論理的地位を曖昧なものにしている。
場の個別物体への作用を「力」という抽象概念にまとめ上げた結果として、運動方程式に両義性が現れる。
解析力学の新しさ
1 質点系全体を単一の力学的対象とする。
2 物質と場の力学が同一の数学的枠組みで記述される。
3力という概念を必ずしも必要としない。
§1.1.2 拘束条件と配位空間
配位空間、一般化座標の概念を定義し、前述の1を達成する。
1.1.3のホロノミック拘束があり、これが時間を陽に含まないスクレロノーマスな場合を考える。
例えば1個の質点があって、運動が円周上に拘束される場合は、

となる。球面上に拘束される場合は

次のように、2質点が円環上を間の距離を保ってぐるぐる回っている拘束もあるかもしれない。

p個の拘束があれば、

3N個のxを、3N-k個とk個に分ける。

ヤコビ行列は

ある点xi=a1,a2,......,a3Nの近傍で、このヤコビ行列のランクがk、すなわちk,k小行列の行列式が0でない、すなわちk,k小行列の逆行列が存在する。

の変数xの前半をq、後半をyとすると、

これをyたちについて解いてyをqの函数として表すことを考える。仮にそれができて、y1,....ykが次のように表せたとすると

これを前の式に代入し、qについて微分すれば、

右辺第2項のk,k行列は正則だったから、逆に解けて、∂y/∂qの値をひとつひとつ確定させることができ、yたちはqたちで表すことができる。

この部分が多変数函数の陰関数定理であるが、『微分積分』(黒田、共立出版)p336あたりに詳しい。陰関数定理の直感的理解は、『キーポイント多変数の微分積分』(小形、岩波)も参考になる。
とにかく、qたちのみパラメタとして系の位置を表すことができる。このqを一般化座標とよぶ。このあたり厳密に書いてありますが、あまり気にしなくて良いかもしれません。ただ、ヤコビ行列は今後多々現れるし、意味をつかんでいた方が良いと思うので、適当な解析本を読んでおくと良いと思います。オススメは上記、黒田と小形
運動はR3Nに埋め込まれたn次元曲面上に限定される。この運動空間を配位空間という。
例えばビーズ振り子p262では、R3に埋め込まれた円周R上を運動する。
§1.4 多様体
§1.4.1
平面は2次元の多様体。
真っ平らなA4の紙に点Qをとる。
Qの座標は、原点をどこかにとれば、x-y座標系や極座標系で表すことができる。このように多様体とは、どこにでも好きなところに、座標系が描けるものなのである。
問 地球は3次元の多様体。地球上の一点である福岡市中央区大濠公園の位置を示すために、座標系を設定してみよ。回答例 中央区役所を原点に南北の距離をとる。など。もちろんグリニッジ天文台を方位角φの原点として極座標を用いることもできる。
ハウスドルフ空間 書いてある通り。位相空間というのがよく分からんが、気にせんで良いとのこと。今度ゆっくり松本多様体で勉強しよう。
同相写像 これも書いてある通り。
ハウスドルフの公理とこの写像のおかげで、多様体上にじかに座標系を書き込めるということ。曲面族のメッシュの図は井田解析力学p9にある。この図もやや抽象的に感じるので、今のところ松本多様体のp2の図のイメージで良いだろう。(一般相対論のときに、イメージをとりなおす。)
§1.4.2
問 以下について説明せよ。
多様体の幾何学的対象
共変性の要請
関数
曲線
曲線は1つの実数tから多様体への連続的な滑らかな写像(微分同相写像)。多分、多様体上に勝手に設定してよい。
曲線は局所座標表示すればc(t)=(q1(t),q2(t),•••)となる
§1.4.3
曲線cに沿う速度ベクトルを考える。
例えば、城南線沿いを走る車の速度である。六本松駅を原点としたxy座標系と、曲座標系では成分が異なってしまうので、直接cをtで微分した値(速度)も異なる。

そこで、城南線に沿う任意の関数、例えば、標高などを取ってきて、いったん実数に写像してその微分を求める。

上の図だとQが六本松近傍なら方向微分は大きく、桜坂とすれば方向微分は小さい。関数はなんでもよく、方向微分作用素として、(1.4.15)と表せる。関数として気温を考えることもできる。その例は山本微分方程式のp158
§1.4.4
Qにおける微分作用素はQを通る曲線ごとに異なるのでvQだのuQだの、いろいろなパターンがあって、それらはベクトル空間の元となっていることが確かめられるから、

微分作用素の集合はベクトル空間を張る。これが接空間である。接空間は場所Qによって異なることに注意する。接空間のベクトルすなわち微分作用素は座標系によらない意味を持つので、幾何学的対象である。その意味において、多様体上の方向微分作用素は"速度ベクトル"なのである。
図は松本多様体p90
§1.4.5
接バンドルは一個の多様体で、その上の点は(Q,vQ)=(qqq...vqvqvq...)て指定される。
ベクトル場は例1.4.1(p63)がわかりやすい。vはQにたいするベクトル値函数でfはスカラー関数である。テンソル値関数に拡張が示唆される。
Q(U上)に基底を取ってくるベクトル値函数(基底ベクトル場)と成分を取ってくるスカラー函数(成分スカラー場?とでもいっておこう)を作用させれば、ベクトル場の局所座標表示1.4.30を得る。下にベクトル場の具体的を示す。

写像vfはQに方向微分vQ[f]を対応付けるが、曲線cはどう考慮したら良いだろうか。方向微分はcに沿った微分のはずなのに、正直「cどこ行ったんや⁈」と思っていたが、vfは「函数」とあるので、作用されるcは任意に指定できるということなのだ。
ベクトル場の基底は共変ベクトル、成分は反変ベクトルの変換則に従う。
§1.4.6
積分曲線は多様体M上の曲線である。
曲線ということは、実数t∈Rから多様体Mへの写像である。1径数変換群は、径数すなわちパラメタを時刻tにとれば運動(移動)を表す写像という意味になる。
積分曲線 多様体上にベクトル場と初期条件を定めると図1.4.5のように曲線が決まる。ベクトル場といってもいろいろなタイプがある。

白線が積分曲線。この曲線はパラメタtから写像された像である。積分曲線c1、c2は例1.4.1の式(1.4.88〜1.4.89)で表される。1.4.36を座標関数q iに作用させると1.4.36プライムを得る。
初期条件は多様体全体にとることができ、tは任意の実数なので、積分曲線は多様体全部を完璧に埋め尽くす。積分曲線上の接ベクトルも多様体全てを埋め尽くすから、これを完備なベクトル場という。
M上の点に運動(動き)を与える写像が1径数変換群だった。1つのパラメタによる変換が連続群をなしている。連続するtそれぞれから変換群の元が生成される。1径数変換の例は1.4.93式にある。
ある1径数変換群の1つの元をフローという。フローは時刻0からtまでの積分曲線にそった動きを与える。この動きはなめらかで連続で逆も連続で、0からtでひとつの動きを定めるといった全単射である。滑らかに連続した元なので、微分同相写像である。
力学の問題を解くということは、t経過したらどこにいるか、どんな速度をもっているか予測するということである。
したがって、「与えられたベクトル場に対する積分曲線を求めるということ」になる。先生のこの極意は表現を変えて至る所に出現するので忘れないように。
試練 次の語句を説明せよ。
ベクトル場
積分曲線
フロー
1径数変換群
いまひとつの例を松本多様体から挙げる。

ノート

§1.5 ベクトルとテンソル
§1.5.1
1ベクトルはベクトルとセットで実数を生む。1ベクトルたちはベクトル空間を張り、基底をもつ。1ベクトル空間の基底はベクトルに作用して成分を取り出すが、それは共役関係である。
§1.5.3
1ベクトルはベクトルひとつを実数に対応させる。ベクトル2つを実数に対応させることを考える。この対応をτとする。
τに与える性質
2重線型写像(双線型写像)
ベクトル空間を張る
2つの1ベクトルのテンソル積である
ベクトルどうしのテンソル積は行列だから、これは納得できる。
1.5.24式のようにテンソル成分(数)と行列状の基底を持つ、行列状の基底は単位ベクトルどうしのテンソル積になっている。もちろん縮約で表されているから、ダミーで和をとる。
τは行列である
τは2階共変テンソルである。
§1.5.4
2階テンソルは1ベクトルの組みを実数に対応させるが、1ベクトルの順を変えると符号も変わるものを2階交代テンソルという。特別に2ベクトルという。
これを歪対称という。交代、反対称でもよい。
同じ1ベクトルどうしの2ベクトル写像はゼロである。
したがって、前節の2階テンソルの形に制約を課して、1.5.38式のように表す。この式はi=1,2 j=1,2とすればすぐに確かめられる。基底の部分が、後で出てくる外積になっていることが分かる。その作用は1.5.38式のように行列式で記憶しておいても良いだろう。
§1.5.5
テンソルの交代化、すなわち、一般的な共変テンソルを反対称テンソルに対応させる写像を考える。これは、交代化作用素A2を定義する。
はじめの式は意味は少々難しいが、τuvと-τvuは同じものということになるということである。だから足して1/2にする。τが1ベクトルのテンソル積ならより具体化できる。結局、交代化作用素は2つの1ベクトルの外積の1/2なのである。
交代化作用素は一般のp階共変テンソルをpベクトルに交代化する。
外積は交代積ともいう。
例えば、1ベクトルどうしのテンソル積からは、2階共変テンソルを得るが、1ベクトルどうしの外積からは2階反対称テンソル、すなわち2ベクトルを得る。
外積はp74最後の式のように、行列式で覚えておくことにする。

2ベクトルはベクトル空間である。
成分Tij 基底ε∧ε
§1.6 微分形式
§1.6.1
Qを通る任意の曲線c(t)があり、Qにおける接ベクトルをvQとする。vQを任意の実数値関数に作用させると実数を得る。いちおう、Qは始点でc(0)=Qとしておく。
この対応を、ベクトルvQから実数への写像dfQと見る。dfQをvQに作用させると実数であり、かつこの写像には線形性があるから。dfQたちはベクトル空間を張る。このdfQが、1ベクトルである。
1ベクトルは∂f/∂qiを成分、dqiを基底とするベクトルである。
dfQ=(∂f/∂qi)dqiと書くことができる。
微分がベクトル量となっている。
fのQにおけるcにそった方向微分が大元となっていて、そこから接空間上のベクトルのfへの作用、さらに1ベクトルのベクトルへの作用と発展していて、以下の式表現がある。

fを座標関数qiとすればdqiは1ベクトルの基底であり、この基底をベクトルvQに作用させると、vQの成分を得る。
一方∂iはベクトルの基底でこれにdfQを作用させると、dfQの成分を得る。
これらが対等な操作であることを表したいならば、双対内積を使って表現する。

§1.6.2
1形式はQにおける1ベクトルを、多様体全部に広げた双対ベクトル場である。
1形式という名から想像できんが、たしかにベクトル場のたぐいである。
あるベクトル場の1形式をω、別のベクトル場の1形式をσとしてこれらはベクトル空間を張る。ベクトル場とベクトル空間を混同してはいけない。ベクトル場はある点Qに作用し接ベクトルvQを像とする写像であり、ベクトル空間はベクトル空間の公理の成り立つ集合である。
1形式はベクトル場と同じく、点Qから1ベクトルdfQを対応づける「場」である。
1形式ωとベクトル場vとの双対内積は関数であって、「ベクトル場vに1形式ωを作用させて得られる関数」という。1.6.20は全て関数であって、Qに作用させてはじめて実数となる。

1形式を用いることで、関数fの全微分や全導関数を表せる。というか、全微分の表現そのものをよく見るとベクトルの成分と基底の線型結合となっているのだ。全導関数の表現はdfをv方向へ射影するということになろうが、もはや抽象的で想像がつかない。

全導関数の導出は丁寧に記載してあるが、自問しながら考えてみると、

1形式はベクトル場に作用させると、函数すなわち0形式となる。x^nの微分がnx^(n-1)とパッと思いつくといったように操作のみに焦点を当てる操作主義の視点から見れば、マシン<ω|●>としておけば良い。●にベクトル場を入れると0形式すなわち関数、何にも入れなければ1形式を表している。
1形式とは何かの関数の全微分dfだから、fがxyzで表されようが、rθφで表されますようが物理的には変わらないはずである。したがって1形式は座標系によらない幾何学的対象であって、共変性をもつ。
§1.6.3
テンソル場はQでテンソルτQを定義する。すなわちτは2階テンソル値函数である。2階テンソル場の成分と基底を表す。
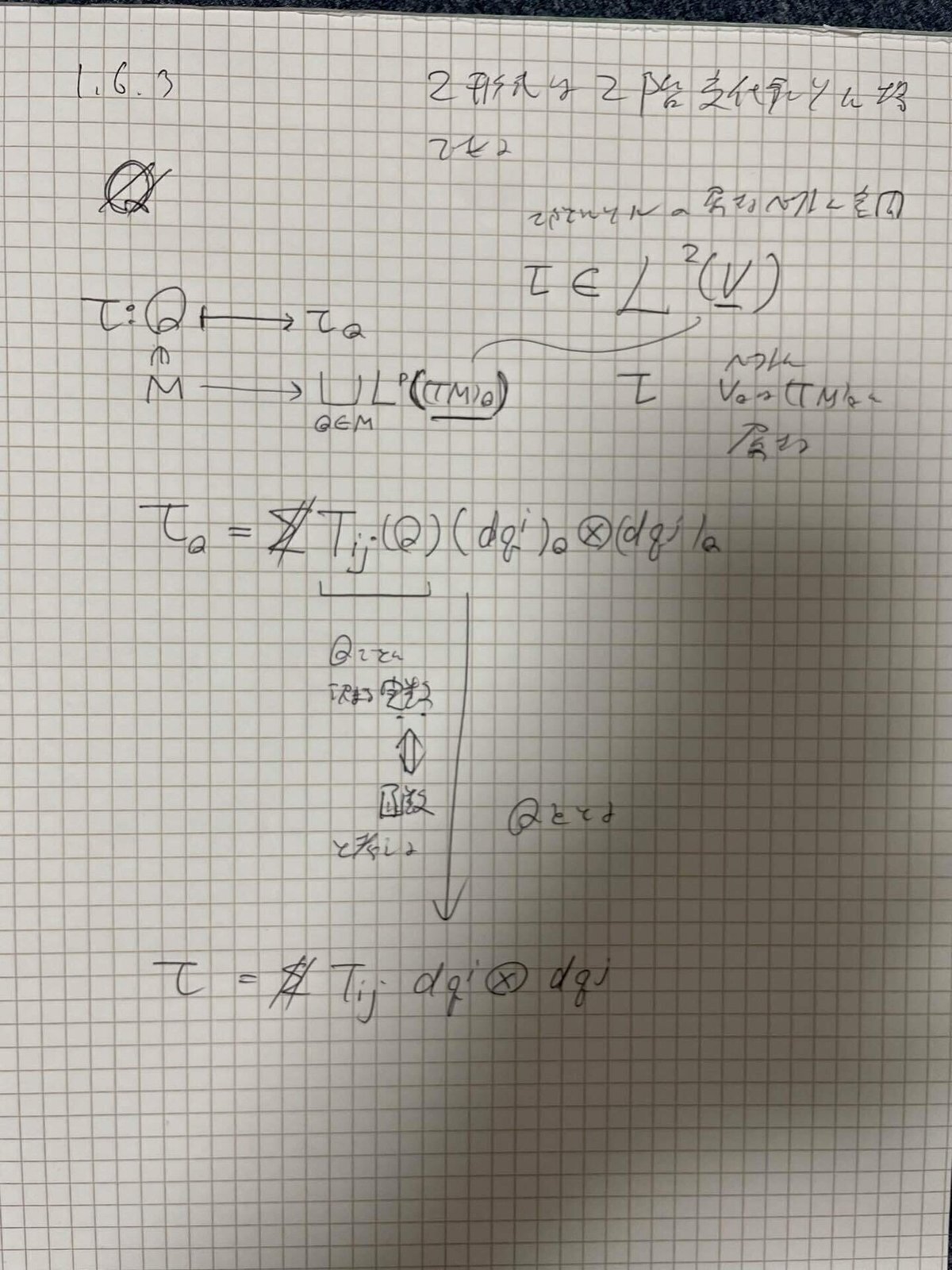
リーマン計量gはM上の2階対称テンソル場であり、Q上に計量テンソルgQを作る。その作用gQ[vQ vQ]すなわちvQどうしの内積を定義すると、正定値である。
リーマン計量を持つ多様体をリーマン多様体ないしリーマン空間という。
簡単にいうと、リーマン計量とは、内積を取れよという写像である。リーマン空間とは内積を持つ空間、多様体である。同じベクトル空間内の積だから内積とよび、双対内積とは異なる。
§1.6.4
微分形式はベクトル場のような直感的な絵を描きにくいので、定義をしっかり理解する。計算していくうちにある種の直感が作られていくという。(松本多様体の基礎)
1形式はQで1ベクトルになるM上のベクトル値函数だった。局所座標表示ではw=wi dqiと表すことができ、1形式を用いて、1.6.17のようにfの全微分を表すこともできる。
1形式とベクトル場の双対内積はひとつの実数値函数であった。2形式と2つのベクトル場との双対内積は1.6.41のように定義され、実数値函数となる。また2形式と1つのベクトル場との双対内積からは1形式を得る。1形式の基底はdqiだが、2形式の基底はdqi∧dqj、成分は2階のテンソル成分である。
§1.6.5
スカラー函数fの外微分はその全微分dfである。df=∂f/∂qi dqiだから、微分形式では成分と基底で表していることになる。微分をベクトル量と認識することが微分形式を理解する鍵だった。
スカラー函数は0形式、その全微分は1形式となる。0形式の外微分は1形式、では1形式の外微分はどうなるか。
これは2形式で、1.6.46で定義する。p形式は共変性をもつから(p83)、1形式の外微分も局所座標系によらない意味を持つことを示さなければならぬ。p89の証明により、とにかく外微分は座標系によらない。
スカラー函数の外微分は勾配である。
1形式の外微分は回転である。
2形式の外微分は発散である。
外微分はベクトル解析の演算を一般化したものなのである。
1.6.46の最後のイコールは、i=1,2 j=1,2の場合を計算すると分かる。

Einsteinの規約に従って和をとると必ず(∂f1/∂q2)dq2^dq1のような項とその逆順のものが表れるからだ。公式として覚えておこうかな。
外微分は局所座標系によらない。p89-L2にさらっと書いてあるが、コレがこの節の核心である。Arnoldによればハミルトン力学は微分形式なしに理解できないことになっているのでこれは肝心だ。p83-下からL3にも、1形式は座標の選び方によらない幾何学的対象であり、ベクトル場とともに、力学を共変的に記述するために必要不可欠な道具である、とあり、見逃せない。

§1.6.6
外微分の四つの公式が示されている。はじめの三つは何となく入る。最後のはライプニッツ規則に余計な(-1)^pが掛けられている。
ポアンカレの補題
Ωが閉形式⇒Ωは完全形式
を説明せよ。
三次元ではrotE=0⇒E=gradφとなりEは保存場、φはポテンシャルである。
§1.6.7
1形式そのものの不定積分のようなものは想像がつかないので、1形式を双対内積によって函数化して、両端の値を入れて、積分値を求める。1.6.61aの2個目のイコールは、
ということと思うが、ω1iのところに(c(τ))があるのが分からない。パラメタが変わっても曲線の形と両端の値が変わらないなら積分値もたぶん変わらんであろう。
2形式の積分はパラメタを2つ用意して、すなわち接ベクトルを2つ用意して、2形式との双対内積から函数化する。その函数は1.6.64で与えられる。1個目のイコールはω2の成分と基底に注意すれば分かる。2個目のイコールは次のようにする。

こうして1.6.65に着く。さらに被積分函数を2次元のデカルト座標に引き戻すと、1.6.68を得る。具体例は解析学の本を読む。いずれもパラメタの選び方によらない積分値を持つ。
ヤコビ行列式は0であってはならない。ヤコビ行列式が正のときは面積分が存在し、多様体は向きづけられている。メビウスの帯は一周目でヤコビ行列式の正負が変わるので向き付けられず、面積は求められない。

多様体上を覆い尽くす座標近傍が重なっているところでヤコビアンが全て正なら向き付けかのうな多様体ということになる。
p形式の積分は公式だけ眺める。
§1.6.8
冒頭、∂Dの向きの決め方を読むのに苦労した。
まずDに対して正の向きを決める。DをM上の2次元超曲面、その局所座標を右手系の(x,y)とし、これをオモテとする。右手を使って、xからyに手を巻いたとき親指が自分に向かってくるなら見ている面はオモテすなわち正ということだ。
境界∂Dの次元は1次元となりパラメタはξ1だが、大濠公園外周のランナーはどちらに回れば正とするかを決めたいのだ。果たしてどちらに周れば正なのか。
そこで、もう一つ次元ξ0を加えるξ0は大濠公園から外に向かう座標とする。(ξ0,ξ1)が右手系を取るようにξ1を決めるならそれが正しい周り方なのだ。左手がお堀の池を向くように走りましょう。実際コースはそう書いてある。
一般化すれば次の手順となる。
領域Dの座標系qを決める。
境界∂Dの座標系ξにもう一つ、外に向かうξ0を加える。
ξが右手系になるようなξ1が正の向き。
スペースコロニーを決める座標系をxyzとすると、コロニー内に住む人の大地はxyを逆転させないなら負の向き(ウラ)に住んでいることになる。
やっと何となく冒頭が理解できた。
多様体上のストークスの定理1.6.70を飲み込むのがこの節の目的である。
例1、1.6.71の一つ目のイコールは1.6.61にあるように、線積分の定義である。二つ目のイコールはp45注釈5と1.4.43により、時間(パラメタ)で微分せいという意味だと思う。
その他の例は、前節の外微分の計算を復習してから見直すが、ストークスの使い方はだいたい分かった。要は1形式とか2形式とか、ωを決めて、その外微分を計算する。これをストークスの定理に入れると、ベクトル解析で出てきた諸定理となる。とても美しい式だ。証明のキモは1.6.78だ。微分形式の外微分は座標によらないことを表している。すなわち外微分という操作は共変的操作である。多様体上で定義された函数、1形式や2形式は外微分で行き来できるから、p30で述べられた幾何学的対象たちだ。座標によらない幾何学的対象となるものが物理量だから、力学はできるだけ多様体上で構築していく方がやりやすいのだ。
余談この節で引き戻しの意味がだんだんつかめてきた。
