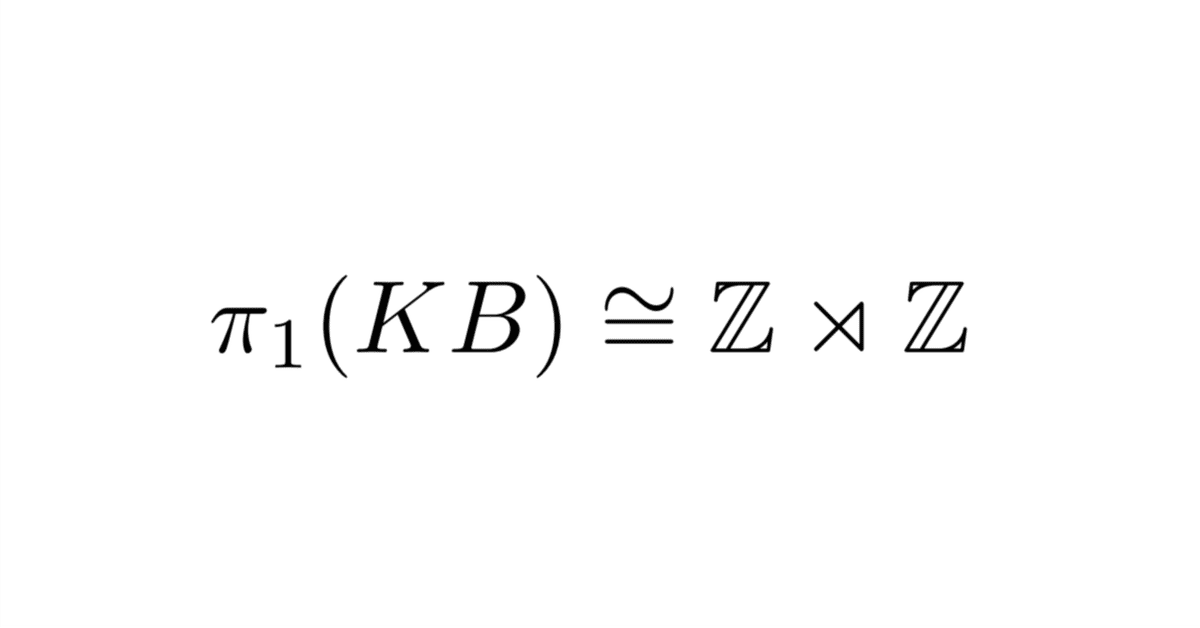
Kleinの壺の基本群
概要
まず初めに結論を述べると
$$
\pi_1\left(KB\right)=\mathbb{Z}\rtimes\mathbb{Z}
$$
となる. ただし$${KB}$$はKleinの壺(Klein bottle)のことである.
これを確かめるために, 以下では「被覆空間作用」(covering space action)と「半直積」(semi-direct product)という概念を導入する. この2つが必要なのは次の定理を利用するためである.
定理([Hatcher, Prop 1.40 (c)])
$${Y}$$: 単連結, 弧状連結, 局所弧状連結, $${G\curvearrowright Y}$$: 被覆空間作用のとき
$${\pi_1\left(Y/G\right)\cong G}$$
これを$${Y=\mathbb{R}^2}$$, $${G=\mathbb{Z}\rtimes\mathbb{Z}}$$の場合に適用すると欲しい結果が得られる. つまり,
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$の定義と$${\mathbb{R}^2/\mathbb{Z}\rtimes\mathbb{Z}\cong KB}$$となること
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が被覆空間作用であること
の順に確かめていけばよい($${Y=\mathbb{R}^2}$$が単連結, 弧状連結, 局所弧状連結であることは簡単にわかる).
半直積について曖昧な人もいるかもしれないので, まずはその定義を確認しておく.
半直積の定義
以下半直積について軽く説明するが, 友人が書いた以下の解説にとても分かりやく定義の気持ちやwell-definednessの説明がある。Wikipediaよりも丁寧だ。
それでは説明に移ろう. はじめに群の自己同型群(Automorphism group)を定義する.
$$
\operatorname{Aut}N\coloneqq\left\{f:N\rightarrow N\middle|f:\text{isomorphism}\right\}
$$
半直積の定義には自己同型群の概念が登場する.
定義(群の半直積)
2つの群$${H}$$, $${K}$$と準同型$${\phi:K\rightarrow\operatorname{Aut}H}$$が与えられたとき, 半直積$${H\rtimes_{\phi}K}$$とは, 集合としては$${H\times K}$$で, 演算が
$${\left(h_1,k_1\right)\cdot\left(h_2,k_2\right)\coloneqq\left(h_1\cdot\phi_{k_1}\left(h_2\right),k_1\cdot k_2\right)}$$
で定義される. ただし$${\phi\left(k_1\right)\in\operatorname{Aut}H}$$を$${\phi_{k_1}}$$と略記している.
群の直積は$${\forall k\in K,\ \phi_{k}=\operatorname{id}_{H}}$$とした特別な場合である. 半直積は通常の直積を$${\phi}$$で"捻った"ものとして捉えることができる.
定義を確認できたので, 次節以降で$${\mathbb{Z}\rtimes\mathbb{Z}}$$が何者であるか, そして$${\mathbb{R}^2}$$への作用の定義を見ていこう.
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$の定義と$${\mathbb{R}^2/\mathbb{Z}\rtimes\mathbb{Z}\cong KB}$$となること 👈👈
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が被覆空間作用であること
ℤ⋊ℤの定義
今回のKleinの壺の基本群を求める場合に必要なのは, 上の半直積の定義で$${H=K=\mathbb{Z}}$$のときである. Abel群$${\mathbb{Z}}$$は$${1}$$(または$${-1}$$)で生成されるので, $${\mathbb{Z}}$$の自己同型は$${1}$$を$${1}$$に写すか$${-1}$$に写すかの2通りのみで, $${\operatorname{Aut}\mathbb{Z}=\left\{\operatorname{id}_{\mathbb{Z}},-\operatorname{id}_{\mathbb{Z}}\right\}}$$である.
このことから非自明な$${\phi:\mathbb{Z}\rightarrow\operatorname{Aut}\mathbb{Z}}$$は
$$
\phi_n=\left(-1\right)^n\operatorname{id}_{\mathbb{Z}}
$$
しかない. ゆえに$${\mathbb{Z}\rtimes_{\phi}\mathbb{Z}}$$は$${\mathbb{Z}\rtimes\mathbb{Z}}$$と略記され, その演算は
$$
\left(m_1,n_1\right)+\left(m_2,n_2\right)\coloneqq\left(m_1+\left(-1\right)^{n_1}m_2,n_1+n_2\right)\quad\left(m_1,n_1,m_2,n_2\in\mathbb{Z}\right)
$$
で与えられる.
では$${\mathbb{Z}\rtimes\mathbb{Z}}$$の$${\mathbb{R}^2}$$への作用を定めよう.
ℤ⋊ℤの作用
念のため一般の群作用の定義を復習する.
定義(群作用)
群$${G}$$の集合$${X}$$への作用(action)とは, 群準同型$${\rho:G\rightarrow\operatorname{Sym}X}$$のことである. ただし$${\operatorname{Sym}X\coloneqq\left\{f:X\rightarrow X\middle|f:\text{bijection}\right\}}$$は$${X}$$の置換群(permutation group)である. しばしば$${\rho\left(g\right)\cdot x}$$を$${g\cdot x}$$と略記する.
$${x\in X}$$に対し, $${G\cdot x\coloneqq\left\{g\cdot x\in X\middle|g\in G\right\}}$$を$${G}$$作用による$${x}$$の軌道(orbit)という.
$${\rho}$$は準同型であるから
$$
e\cdot x=x,\ \ \left(gh\right)\cdot x=g\cdot\left(h\cdot x\right)
$$
が成り立つ.
では本筋に戻ろう. $${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$を次で定める.
$$
\left(m,n\right)\cdot\left(x,y\right)\coloneqq\left(\left(-1\right)^nx+m,y+n\right)\quad\left(m,n\in\mathbb{Z}\right)
$$
これは以下の計算で確かめられる通り, 実際に群作用である.
$$
\begin{aligned}
\left(0,0\right)\cdot\left(x,y\right)=&\left(\left(-1\right)^0x+0,y+0\right) \\
=&\left(x,y\right) \\
\end{aligned}
$$
$$
\begin{aligned}
\left(m_1,n_1\right)\cdot\left(\left(m_2,n_2\right)\cdot\left(x,y\right)\right)=& \left(m_1,n_1\right)\cdot\left(\left(-1\right)^{n_2}x+m_2,y+n_2\right) \\
=& \left(\left(-1\right)^{n_1+n_2}x+m_1+\left(-1\right)^{n_1}m_2,y+n_1+n_2\right) \\
=& \left(m_1+\left(-1\right)^{n_1}m_2,n_1+n_2\right)\cdot\left(x,y\right)
\end{aligned}
$$
一方Kleinの壺$${KB}$$は$${\mathbb{R}^2}$$を以下の同値関係で割ることによって得られる.
$$
\left\{
\begin{aligned}
\left(x,y\right) & \sim\left(x+m,y+2k\right) \\
\left(x,y\right) & \sim\left(-x+m,y+\left(2k-1\right)\right)
\end{aligned}
\right.
\quad\left(m,n,k\in\mathbb{Z}\right)
$$
これは$${\mathbb{Z}\rtimes\mathbb{Z}}$$の作用
$$
\left(m,n\right)\cdot\left(x,y\right)\coloneqq\left(\left(-1\right)^nx+m,y+n\right)
$$
によって同じ軌道(orbit)に属する点を同一視することに他ならない. したがって
$$
\mathbb{R}^2/\mathbb{Z}\rtimes\mathbb{Z}\cong KB
$$
が成り立つ.
最後に, 次節で被覆空間作用の定義と$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が実際に被覆空間作用であることを確認する.
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$の定義と$${\mathbb{R}^2/\mathbb{Z}\rtimes\mathbb{Z}\cong KB}$$となること
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が被覆空間作用であること 👈👈
被覆空間作用
被覆空間作用では, 以下の定義のように群が位相空間に作用する.
定義(covering space action)
$${G}$$を群, $${Y}$$を位相空間とする. 群作用$${G\curvearrowright Y}$$が
(☆) $${\forall y\in Y, y\in\exists U\underset{\text{open}}{\subset}Y, g_1\neq g_2\implies g_1\cdot U\cap g_2\cdot U=\emptyset}$$
という性質を満たすとき, 被覆空間作用(covering space action)という.
名前の由来は任意の位相空間$${X}$$について, その被覆空間$${\tilde{X}}$$に作用するデッキ変換群$${G(\tilde{X})}$$が(☆)の性質を満たすからである. 詳細についてはページ一番下の参考文献の[Hatcher]を参照してほしい.
この定義の表記法に従えば, $${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が被覆空間作用であることは次のように確認できる.
任意の$${\left(x,y\right)\in\mathbb{R}^2=Y}$$と$${G=\mathbb{Z}\rtimes\mathbb{Z}}$$の異なる元$${g_1=\left(m_1,n_1\right)}$$, $${g_2=\left(m_2,n_2\right)}$$に対し, その十分近傍$${U=D_{\epsilon}\left(x,y\right)\coloneqq\left\{\left(x^{\prime},y^{\prime}\right)\in\mathbb{R}^2\middle|\ |\left(x,y\right)-\left(x^{\prime},y^{\prime}\right)|<\epsilon\right\}}$$($${\epsilon>0}$$は十分小)をとってくれば, $${\left(m_1,n_1\right)\cdot D_{\epsilon}\left(x,y\right)}$$と$${\left(m_2,n_2\right)\cdot D_{\epsilon}\left(x,y\right)}$$が共通部分を持たないようにできる.
非常に長ったらしいが, 1つずつ丁寧に順を追えば当たり前のことを言っているに過ぎない.
まとめ
以上で
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$の定義と$${\mathbb{R}^2/\mathbb{Z}\rtimes\mathbb{Z}\cong KB}$$となること
$${\mathbb{Z}\rtimes\mathbb{Z}\curvearrowright \mathbb{R}^2}$$が被覆空間作用であること
が確認できた. よって
$$
\pi_1\left(KB\right)=\mathbb{Z}\rtimes\mathbb{Z}
$$
が成り立つ.
参考文献
[1] A. Hatcher. "Algebraic Topology." Cambridge University Press. 2001. available at: https://pi.math.cornell.edu/~hatcher/AT/AT.pdf
