量子ゲートの分解のはなし

Introduction

あるオラクルを実現する標準的なテクニックは、その表現行列を1 Qubitの量子ゲートやCNOTゲートといったより単純なゲートの表現行列の積に分解することです。分解の計算方法はさまざま知られていますが、例えばLi, Pelejoによるrecurrence schemeなどが有名だと思います。今回は、この計算スキームのアイディアを2 Qubitの量子ゲートを例に説明しましょう。

なお、このノートは量子コンピュータ Advent Calendar 2018, 20日目の記事です。作成者の@gyu-donさんに感謝申し上げます。

unitary行列の分解

2 Qubitの量子ゲートに対する表現行列は4次のunitary行列です。このunitary行列を2次のunitary行列の積に分解する計算方法を紹介し、量子ゲートの表現行列という観点に注目することで気づく問題点を述べます。

4次のunitary行列には次のような分解を考えることができます。ヒントはガウスの消去法です。

この因数分解の計算からn Qubitの量子ゲートの表現行列もまた、高々NC2個(N=2のn乗)の2次unitary行列を含むn次正方行列の積に分解できることがわかります。（今回はn = 2なのでN=4。2 Qubitの量子ゲートの表現行列は、高々4C2=6個の2次unitary行列を含む4次正方行列の積で書ける。）

ところで、この分解計算をオラクルの量子ゲートとしての実現方法を得るための計算いう当初の目的に立ち戻ってみると、ある問題点が浮かび上がることに気づきます。分解に現れる行列の形を列挙してみましょう。

行列type 1, type 2はそれぞれ1 Qubitに対する何らかの量子ゲートから定義されるcontrolled unitary gateの表現行列だとわかりますが、type 5はcircuitを跨っていてどのような量子ゲートの表現行列なのか明らかではありません。以下では、この点の修正方法を説明します。

量子ゲートの表現行列によるunitary行列の分解

量子ゲートの実現に上の分解計算を応用するなら、事前に分解する行列をcontrolled unitary gateの表現行列に制限してから考えるのが妥当でしょう。4次のunitary行列であれば、次の4種類の2次のunitary行列を含む4次正方行列に分解する問題を、上の方法を参考に考えることになります。

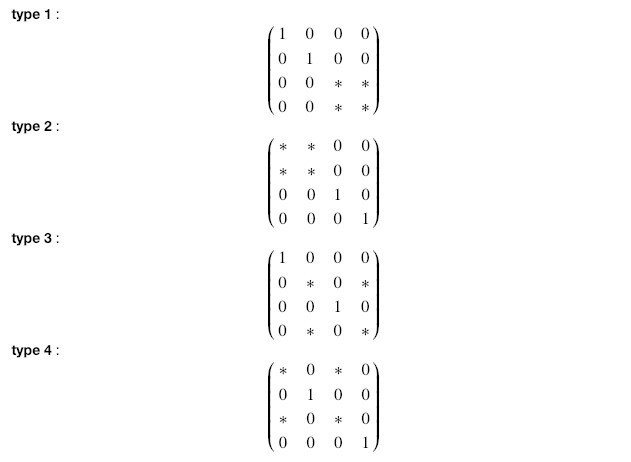
上記の表現行列に対して、量子ゲートによる実現はそれぞれ次のようになります。（左からtype 1, type 2, type 3, type 4です。論文[LP]から引用。）

実際に今回は、type 1, type 2, type 3の3種類のunitary行列を用いることで4次unitary行列の分解を求めることができます。以下がその計算方法です。

ここで、行列U31, U32, U34がtype 1、行列U21がtype 2、行列U43, U42がtype 3です。ゆえに任意の2 Qubitの量子ゲート（4次unitary行列）に対して、controlled unitary gateによる実現が得られました。

recurrence scheme

今回は2 Qubitの量子ゲートを1 Qubitの量子ゲートから定義されるcontrolled gateの積に分解する計算を示しました。これと同様に考えることで、n Qubitの量子ゲートが(n-1) Qubitの量子ゲートから定義されるcontrolled unitary gateに分解できることを示すことができます。この分解計算を再帰的に繰り返すことで、1 Qubitの量子ゲートと2 Qubitのcontrolled unitary gateへの分解に落とすことができます。

おわりに

本来、このアルゴリズムによる行列分解が必要最小限のゲート数を与えるかなどもまた大きな興味の対象ですが、この辺りについては追って調べていきたいと思っているところです。また、説明が雑な部分があり気になっているので、あとでまた書き直していければと思います。それでは。

参考文献

[LP] C. K. Li and D. C. Pelejo, Decomposition of Quantum Gates, International Journal of Quantum Information Vol.12, 1450002 (2014).
[LYR] C. K. Li, X. Yin and R. Roberts, Decomposition of Unitary Matrices and Quantum Gates, International Journal of Quantum Information Vol 11, 1350015 (2013).
[VMBS] J. Vartiainen, M. Mottonen, V. Bergholm and M. Salomaa, Quantum Circuits for General Multiqubit Gates, Physical Review Letters 93 (13), 130502 (2004).