【ベクトル解析】3次元極座標（球座標）のナブラ演算子とラプラシアンの、実用的で簡単な導出方法（学部１，２年生向け）

こんにちは。胡乱布団です。

先日、我らがヨビノリさんが球座標ラプラシアンについての動画をアップしていました。

この動画で紹介されている方法は、もっとも初歩的なやり方で、３次元デカルト座標の微分演算子をもとにチェインルールを用いて、導出するものです。
そのため、理屈的に難しいことはないのですが、いかんせん、計算量が多い……。

そこで、今回はもう少し楽に球座標でのナブラ演算子、ラプラシアンを求められる方法を紹介したいと思います。

＊対象は、理系の学部１年生、２年生（ただし数学科を除く）くらいを対象にしています。

＊＊本記事のpdfファイルを販売しています。（詳細は記事の最後に）よろしければ、ご購入ください。

球座標におけるナブラは定義から求めるのが楽。

球座標におけるナブラは、ナブラの定義から求めるのが楽です。

微分可能なスカラー函数$${f}$$に対して、ナブラは次を満たします。

これはいわゆる方向微分ですね。

さて、球座標の微小変化$${d\bm{r}}$$は、次のように書けました。

ここから、$${\nabla f\cdot d\bm{r}}$$は、

$$
\begin{equation*}
\nabla f\cdot d\bm{r} = (\nabla f)_rdr+(\nabla f)_\theta rd\theta+(\nabla f)_\varphi r\sin\theta d\varphi
\end{equation*}
$$

となります。

いっぽう、全微分は偏微分を用いて次のように書けます。

この２式は等号で結ばれるので辺々を比較すると、

となり、

を得ることができます。

どうです？　簡単でしょう？

球座標ラプラシアンは、球座標では単位ベクトルの微分を考えると、楽。

デカルト座標のようにはいかないわけ（重要）

球座標におけるナブラが求められたので、次はラプラシアンを求めていきます。ラプラシアンは次のように定義されました。

$$
\begin{equation*}
\Delta \equiv \nabla\cdot\nabla
\end{equation*}
$$

なーんだ、たださっきの微分演算子の各成分を偏微分すればいいだけじゃん！

…………だったら、どれだけ楽だったことか……………。

そうです。球座標においては、ただ各成分を偏微分するだけでは正しいラプラシアンは得られません。

なぜなら、球座標では単位ベクトルが定ベクトルではないから。

３次元デカルト座標であれば、座標の位置に依らず、$${(x,y,z)}$$においても単位ベクトルはそれぞれ座標軸のほうに取ることで、$${(1,0,0),(0,1,0),(0,0,1)}$$となりますが、３次元球座標では位置によって単位ベクトルも変わってしまいます。

極端な例で考えましょう。$${(x,y,z)=(1,0,0),(0,0,1)}$$でそれぞれ動径方向の単位ベクトル$${\bm{e}_r}$$を考えます。

前者では、動径は$${x}$$軸方向を向いているので、デカルト座標で表すと、$${\bm{e}_r=(1,0,0)}$$と取れます。
いっぽうで、後者では、動径は$${z}$$軸方向を向いているので、単位ベクトルは$${\bm{e}_r=(0,0,1)}$$と取れます。

ほら、単位ベクトルが変化した！！！！

ですので、先の内積を考えるときには、単位ベクトルの微分を考える必要があります。

球座標の単位ベクトルの微分を考える。

まず、球座標の３つの単位ベクトルを３次元デカルト座標で表します。

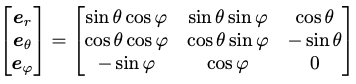
学部１年生や苦手な人向けに、これの導出の考え方を簡単に説明しておきます。
上の３つの単位ベクトルを得るためには、実は、３つとも考える必要はなくて、$${\bm{e}_r}$$だけ求められれば、ほかの２つも簡単に求めることができます。

$${(r,\theta,\varphi)=r\bm{e}_r}$$だから、まず、$${\bm{r}(=r\bm{e}_r)}$$の$${xy}$$平面への正射影を考えると、その大きさは$${r\sin\theta}$$になります。
次に、これの$${x}$$軸、$${y}$$軸への正射影を考えることで、$${x}$$座標、$${y}$$座標を得ることができます。
これらはそれぞれ、$${r\sin\theta\cos\varphi}$$、$${r\sin\theta\sin\varphi}$$となります。
$${z}$$座標はもっと簡単で、$${\bm{r}}$$の$${z}$$軸への正射影を考えることで、$${r\cos\theta}$$と得ることができ、最後に大きさ$${r}$$で割ることで、動径方向の成分表示を得ることができました。

さて、ここから$${\bm{e}_\theta,\bm{e}_\varphi}$$を求める方法ですが、これは直感的に考えれば簡単で、それぞれの単位ベクトルは、$${\bm{e}_r}$$を$${\theta}$$方向、$${\varphi}$$方向に微分したものに比例します。
つまり、$${\bm{e}_r}$$を偏微分すれば良いのです。

さて、この座標表示を用いて、各単位ベクトルの微分を求めておきましょう。それは次のようになります。

準備完了

準備は整ったので、あとは計算するのみです。ここで注意するのは、内積はちゃんと分配して積の微分を実行することです。

$$
\begin{align*}
\Delta &=\nabla\cdot\nabla\\
\\
&=\biggl(\dfrac{\partial}{\partial r}\bm{e}_r + \dfrac{1}{r}\dfrac{\partial}{\partial \theta}\bm{e}_\theta + \dfrac{1}{r \sin\theta}\dfrac{\partial}{\partial \varphi}\bm{e}_\varphi\biggl)\cdot\biggl(\dfrac{\partial}{\partial r}\bm{e}_r + \dfrac{1}{r}\dfrac{\partial}{\partial \theta}\bm{e}_\theta + \dfrac{1}{r \sin\theta}\dfrac{\partial}{\partial \varphi}\bm{e}_\varphi\biggl)\\
\\
&= \dfrac{\partial^2}{\partial r^2} + \dfrac{2}{r}\dfrac{\partial}{\partial r}+ \dfrac{1}{r^2}\dfrac{\partial^2}{\partial \theta^2} + \dfrac{\cos{\theta}}{r^2 \sin{\theta}}\dfrac{\partial}{\partial \theta} + \dfrac{1}{r^2 \sin^2{\theta}}\dfrac{\partial^2}{\partial \varphi^2}\\
\\
&= \dfrac{1}{r^2}\dfrac{\partial}{\partial r}\biggl(r^2\dfrac{\partial}{\partial r}\biggl) + \dfrac{1}{r^2\sin{\theta}}\dfrac{\partial}{\partial \theta}\biggl(\sin{\theta}\dfrac{\partial}{\partial \theta}\biggl)+\dfrac{1}{r^2 \sin^2{\theta}}\dfrac{\partial^2}{\partial \varphi^2}
\end{align*}
$$

のように、デカルト座標からチェインルールを使うよりかは、少しだけ楽に求めることができました。

最後に、有料で球座標ラプラシアンの導出について書かれたpdfファイルをマガジンにて、￥150で販売しています。

（わたしのポリシーとして、科学的知見は無償で公開されるべきだと思っているので、この記事だけで完結するようには書いてあります。
ちょっとでも、わたしを応援たいな、とか、多少見やすいかもしれないpdfファイルがほしい方向けに販売しています）

内容は、本記事に書かれた内容（pdfなので多少見やすいかも？）と、おまけとして、発展事項にはなりますが、学部２、３年生以上向けの、もっと手早くラプラシアンを求める方法を追記しました。
よろしければご購入ください。