ペケとジマの複素解析 #(完) 無限遠点の留数

コジ

2024年11月18日 04:01

登場人物

ペケ
理系，学部2年．
苗字が無い．

ジマ
文系，ペケの先輩．
苗字が島(ジマ)．

ペケ：あれ，今回で最後？

ジマ：今回で複素積分はほぼほぼ完成だね．ペケくんは工学部だから，せいぜいテストには今回までの内容しか出ないと思うよォー．

ペケ：そうですか．なんだか寂しいですね．

ジマ：まー，気が向いたら教えてやるよ．
さて，今日は今まで誤魔化してたところを一挙に解説していく．

ペケ：最後の最後でですか．

ジマ：別に理屈わかんなくても問題は解けるからねー．
まずは#4で話した，
「ある極を囲う複素積分は経路によらず，囲った回数×$${2\pi i}$$×留数で表される」という話だ．

ペケ：あー，頭とケツが合ってなくても同じ積分結果になるってやつですか．

ジマ：Soー．下の経路を見てくれ．

例によって本来$${C_2}$$と$${C_4}$$は重なってるけど見やすさのため離してるよー．
#4でやってた経路変換は$${C_1}$$から$${C_3}$$にすることだってのは分かるな？

ペケ：はい．てことは，コーシーの定理より，極を避けた積分経路$${C_1+C_2-C_3+C_4}$$の積分はゼロになって，$${C_4=-C_2}$$だから

$$
\begin{aligned}
0&=\oint_{C_1+C_2-C_3+C_4}f(z)\mathrm dz\\
&=\oint_{C_1+C_2-C_3-C_2}f(z)\mathrm dz\\
&=\int_{C_1-C_3}f(z)\mathrm dz\\
&=\int_{C_1}f(z)\mathrm dz+\int_{-C_3}f(z)\mathrm dz\\&=\int_{C_1}f(z)\mathrm dz-\int_{C_3}f(z)\mathrm dz\\
\\
&\therefore \int_{C_1}f(z)\mathrm dz=\int_{C_3}f(z)\mathrm dz
\end{aligned}
$$

ということなんですね？
あ，これと同じことを各極に対してするから，複素積分は積分経路が囲った極の留数の和になるのか．

ジマ：気づいたね．だから結局，複素積分は経路とその頭とケツが問題なのではなく，留数と極を囲った回数が重要になってくるんだyoー．Soー．

ペケ：この性質から，$${C_3}$$の半径はほかの極に被らないように無限に小さくできるのも面白いですね．

ジマ：Soー．では最後にこの積分を解いてくんね？

$$
\begin{aligned}
\int_0^1\sqrt{x(1-x)} \ \mathrm dx
\end{aligned}
$$

ペケ：これは高校レベルですね．

$$
\begin{aligned}
\int_0^1\sqrt{x(1-x)} \ \mathrm dx
&=\int_0^1\sqrt{\left(\frac12\right)^2-\left(x-\frac12\right)^2} \ \mathrm dx\\
\end{aligned}
$$

で，これが中心$${(1/2,0)}$$半径$${1/2}$$の円の上半分の部分の面積だから，$${\pi/8}$$ですね？

ジマ：テクいw 計算サボりやがったw
じゃこれを複素積分を用いて解いて本講座の締めとしよう．

$$
\begin{aligned}
\oint_{ダンベル}\sqrt{z(1-z)} \ \mathrm dz
\end{aligned}
$$

積分経路は次だよー．$${(r > 0)}$$

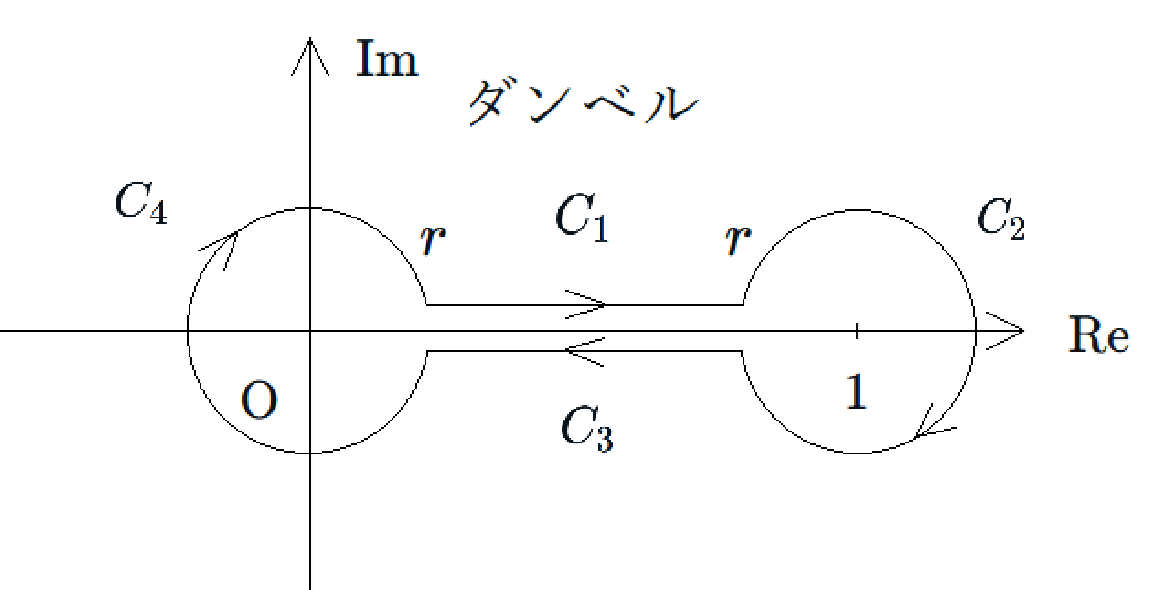
何度もしつこく言っていくが，例によって本来$${C_1}$$と$${C_3}$$は重なってるけど見やすさのため離してるよー．

ペケ：まずは留数計算だけど，「ダンベル」の中に極はないからゼロでしょ？

ジマ：ｸｸｸｸｸ…www

ペケ：？
で，$${C_4}$$は，

$$
\begin{aligned}
\left|\int_{C_4}\sqrt{z(1-z)} \ \mathrm dz\right|
&\leq \int_{C_4}\left|\sqrt{z(1-z)} \ \mathrm dz\right|\\
&= \int_{2\pi}^0\left|\sqrt{re^{i\theta}(1-re^{i\theta})} \ ire^{i\theta}\mathrm d\theta\right|\\
&= \int_0^{2\pi}\left|\sqrt{re^{i\theta}(1-re^{i\theta})} \ ire^{i\theta}(-\mathrm d\theta)\right|\\
&= \int_0^{2\pi}\left|-r^{3/2}\sqrt{(1-re^{i\theta})} \ e^{i\theta/2}ie^{i\theta}\mathrm d\theta\right|\\
&= \int_0^{2\pi}r^{3/2}\left|\sqrt{(1-re^{i\theta})}\right|\mathrm d\theta\\
&= \int_0^{2\pi}r^{3/2}\left|1-\frac12re^{i\theta}+\cdots\right|\mathrm d\theta\\
&\leq \int_0^{2\pi}r^{3/2}\left(|1|+\left|-\frac12re^{i\theta}\right|+\cdots\right)\mathrm d\theta\\
&(\because 三角不等式)\\
&= \int_0^{2\pi}r^{3/2}\left(1+\frac12r+\cdots\right)\mathrm d\theta\\
&=2\pi r^{3/2}\left(1+\frac12r+\cdots\right)
\end{aligned}
$$

で，

$$
\lim_{r\rightarrow+0}2\pi r^{3/2}\left(1+\frac12r+\cdots\right)=0
$$

だから，

$$
\therefore\lim_{r\rightarrow+0}\int_{C_4}\sqrt{z(1-z)} \ \mathrm dz=0
$$

次に， $${C_2}$$は，

$$
\begin{aligned}
\left|\int_{C_2}\sqrt{z(1-z)} \ \mathrm dz\right|
&\leq \int_{C_2}\left|\sqrt{z(1-z)} \ \mathrm dz\right|\\
&= \int_0^{-2\pi}\left|\sqrt{(1-re^{i\theta})re^{i\theta}} \ (-ire^{i\theta}\mathrm d\theta)\right|\\
&(z=1-re^{i\theta}と置換)\\
&= \int_{-2\pi}^0\left|\sqrt{(1-re^{i\theta})re^{i\theta}} \ ire^{i\theta}\mathrm d\theta\right|\\
&\leq2\pi r^{3/2}\left(1+\frac12r+\cdots\right)
\end{aligned}
$$

で，さっきと同じだから，

$$
\therefore\lim_{r\rightarrow+0}\int_{C_2}\sqrt{z(1-z)} \ \mathrm dz=0
$$

でいつも通り最後に$${C_1+C_3}$$を計算するんですが，$${C_3}$$の$${r,1-r}$$は$${C_1}$$より偏角が$${-2\pi}$$進んでることに注意すると，$${re^{-2\pi i},(1-r)e^{-2\pi i}}$$と書けることから，

$$
\begin{aligned}
&\int_{C_1}\sqrt{z(1-z)} \mathrm dz+\int_{C_3}\sqrt{z(1-z)} \mathrm dz\\
&=\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz＋\int_{(1-r)e^{-2\pi i}}^{re^{-2\pi i}}\sqrt{z(1-z)}\mathrm dz\\
&=\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz＋\int_{1-r}^{r}\sqrt{ue^{-2\pi i}(1-ue^{-2\pi i})} \ e^{-2\pi i}\mathrm du\\
&(z=ue^{-2\pi i}と置換)\\
&=\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz-\int_r^{1-r}e^{-\pi i}\sqrt{u(1-u)} \ \mathrm du\\
&=\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz+\int_r^{1-r}\sqrt{u(1-u)} \ \mathrm du\\
&=2\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz
\end{aligned}
$$

最後に留数と等置して，

$$
\begin{aligned}
0
&=2\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz
+\int_{C_2+C_4}\sqrt{z(1-z)} \ \mathrm dz
\end{aligned}
$$

$${r\rightarrow+0}$$とすると，

$$
\begin{aligned}
&0=2\int_0^1\sqrt{z(1-z)}\mathrm dz+0+0\\
\\
&\therefore\int_0^1\sqrt{z(1-z)}\mathrm dz=0
\end{aligned}
$$

・・・あれぇ？

ジマ：ｳﾍﾍﾍﾍﾍﾍﾍ！！！！

ペケ：$${\pi/8}$$になるはずなのに．どっかミスってました？

ジマ：頭っからミスってるよォーwww

ペケ：何度も読み返しましたが，分かんないです．

ジマ：そらそうよ．教えてないんだもん．
実は，無限遠点にも留数があるんだよォーw

ペケ：へぇー！想像もしなかったですね．Wiiスポーツで場外にあるミカンとかパンの形の的を発見した時のような感じです．
今まで目の前の的(複素数平面上に見える極)ばっかりに目が行ってましたが，場外(無限遠点)にも的があったなんてっていう感覚．

ジマ：次で計算できるよー．

$$
{\underset{z=\infty}{\mathrm{Res}}}f(z)={\underset{z=0}{\mathrm{Res}}}\left(-\frac1{z^2}\right)f\left(\frac1z\right)
$$

ペケ：えーと，「ダンベル」は反時計回り$${-1}$$周だから，$${-1}$$×$${2\pi i}$$×留数になるから…

ジマ：待った．極がダンベルの外側だから$${2\pi i}$$×留数だわ．

ペケ：なんでですか？

ジマ：n～～．何て言えばいいかな．「ダンベル」の外側がリーマン球面の北極$${{z=\infty}}$$を反時計回りに囲ってるっていうイメージなんだよねー．

$$
\begin{aligned}
&\oint_{|z|=\infty,反時計回り1回転}f(z)\mathrm dz\\
&=\oint_{|w|=+0,反時計回り-1回転}\left(-\frac{1}{w^2}\right)f\left(\frac{1}{w}\right)\mathrm dw\\
&\left(z=\frac{1}{w},\arg(w)=0から-2\pi\right)
\end{aligned}
$$

試しに

$$
\begin{aligned}
\oint_{|z|=1}\frac1z \mathrm dz
\end{aligned}
$$

が積分経路の内側の$${z=0}$$を反時計回り$${1}$$回囲ってると解釈すると，

$$
\begin{aligned}
\oint_{|z|=1,反時計回り1回転}\frac1z \mathrm dz
&=2\pi i \ {\underset{z=0}{\mathrm{Res}}}\frac1z\\
&=2\pi i \ \lim_{z\rightarrow0}1\\
&=2\pi i
\end{aligned}
$$

積分経路の外側の$${z=\infty}$$を反時計回り$${-1}$$回囲ってると解釈すると，

$$
\begin{aligned}
\oint_{|z|=1,反時計回り1回転}\frac1z \mathrm dz
&=(-1)\cdot2\pi i \ {\underset{z=\infty}{\mathrm{Res}}}\frac1z\\
&=-2\pi i \ {\underset{z=0}{\mathrm{Res}}}\left(-\frac{1}{z^2}\right)\frac{1}{1/z}\\
&=2\pi i \ {\underset{z=0}{\mathrm{Res}}}\frac1z\\
&=2\pi i \ \lim_{z\rightarrow0}1\\
&=2\pi i
\end{aligned}
$$

でちゃんと一致するじゃん？

ペケ：あ，はい．もしかして，$${C}$$を反時計回り1周として，

$$
2\pi i(Cが囲う留数の和)
=\oint_Cf(z)\mathrm dz
=(-1)\cdot2\pi i(Cの外側の留数の和)
$$

ですか？

ジマ：そぉー．よく気づいたな．てことは？

ペケ：てことは，右辺を左辺に移行すると，ゼロになるから，複素数平面全体の留数の和がゼロになるんですね．へー！

ジマ：今回のように，内部の留数の計算がムズいときに使えるな．続きどうぞ．

ペケ：はい．

$$
\begin{aligned}
&\oint_{ダンベル}\sqrt{z(1-z)} \ \mathrm dz\\
&=2\pi i \ {\underset{z=\infty}{\mathrm{Res}}}\sqrt{z(1-z)}\\
&=2\pi i \ {\underset{z=0}{\mathrm{Res}}}\left(-\frac1{z^2}\right)\sqrt{\frac1z\left(1-\frac1z\right)}\\
&=-2\pi i \ {\underset{z=0}{\mathrm{Res}}}\frac{\sqrt{z-1}}{z^3}\\
&=-2\pi i \ \frac{1}{2!}\lim_{z\rightarrow0}\frac{\mathrm d^2}{\mathrm d^2z}\left(\frac{\sqrt{z-1}}{z^3}\cdot z^3\right)\\
&=-\pi i \ \lim_{z\rightarrow0}\frac{1}{2}\left(-\frac12\right)(z-1)^{-3/2}\\
&=\pi i\frac{(-1)^{-3/2}}{4}\\
&=\pi i\frac{(e^{-\pi i})^{-3/2}}{4}\\
&=\pi i\frac{e^{3\pi i/2}}{4}\\
&=\pi i\frac{-i}{4}\\
&= \frac{\pi}{4}\\
\end{aligned}
$$

だから，

$$
\begin{aligned}
\frac{\pi}{4}=2\int_r^{1-r}\sqrt{z(1-z)}\mathrm dz
+\int_{C_2+C_4}\sqrt{z(1-z)} \ \mathrm dz
\end{aligned}
$$

両辺$${r\rightarrow+0}$$とすると，

$$
\begin{aligned}
&\frac{\pi}{4}=2\int_0^1\sqrt{z(1-z)}\mathrm dz+0\\
\\
&\therefore\int_0^1\sqrt{z(1-z)}\mathrm dz=\frac{\pi}{8}
\end{aligned}
$$

ですね？