
トランプのカードはいつ混ざるか
天才Yさんからまた面白い課題が降ってきた。
「トランプのカードが混ざっているってどういう状態?」「綺麗に並んだトランプをシャッフルするといつからよく混ざった状態になるの?」
よーし、いっちょやってみるか!
考察の手順
次の手順で考えよう。トランプ52枚を重ねた「山」(スタック)に対して
並びの乱雑さをどうやって数値評価するか?
「よく混ざったカードの山」とはどういう状態か?
何回くらい混ぜると「よく混ざる」か?
1) 「山」の並びの乱雑さを数値化する
山の並びが乱雑であるという状態がピンとこなかったので、逆の「山の並びが乱雑ではない」という状態を考えてみた。例えば、カードを一枚ずつめくっていって、♥3の次が♥4だったり、♠Kの次が♦Kだったりしたら、「このカード本当に混ざってるの?」と疑問に思うのではないか。
そこで、まずカード2枚の組の類似性を表現する値「距離」を定義する。
【カード間の距離】
定義:2枚のカードがあるとき、その距離を「数字の差」と「マークの同・違」から計算する。
・マークが同じ時は数字の差の絶対値が距離
・マークが違う時はさらに+1
・A=1, J=11, Q=12, K=13として計算
・AとKは繋がっていないとする
例)
・♥3と♠Kは、数字が13-3=10違い、マークも違うので、距離は11
・♥3と♥Kは、数字が13-3=10違い、マークが同じなので距離は10
・一番近いのは距離1 例♥3/♥4や♠K/♥Kなど
・一番遠いのは距離13 例♥A/♠Kなど
次に山のスコアを定義する
【山のスコア】
定義:「山」の52枚のカードの隣接する51組に対し、それぞれ「距離」を計算。その総和を「山」のスコアとする。
このやり方では、隣接したカード以外の類似性は考慮しない。
例:隣接せずに規則性を持って並んでいる場合
(例えば♥3、♠K、♥4、♠Q、♥5、♠Jなど)について、
一個おきのカードの「近さ」は関知しない。
いくつか練習。
・最小のスコアは51。7並べの完成図を一筆書きする要領で辿る。
たとえば:
♠A23...K ♣KQJ...A ♥A23...K ♦KQJ...Aは、全ての組が距離1なのでスコアは51。(後のシミュレーションの初期値として使う)
♠A♣A♥A♦A ♦2♥2♣2♠2 ♠3...♠Q♠K♣K♥K♦Kも
全ての組が距離1なのでスコア51。
・♠A23...K ♣A23...K ♥A23...K ♦A23...K
の方が(人間には)一見乱雑さが少ないように見えるが、K→Aのジャンプのコストが高いので、こちらはスコアは87になる。
・最大のスコアはいくつだろうか?(387まで行くことは確認済)
ちなみに、
このようなペアの間の乱雑さを調べて、列の乱雑さを評価する方法を「ペア検定」というらしい(by chatGPT)。しかし、そのような言葉で検索しても何も出てこないので、英語の用語なのかも知れない。
2) 「よく混ざったカード」とは?
「よく混ざった山」とは、これ以上カードを混ぜてもスコアがあまり変化しない状態、と考えられる。
先ほど例に挙げたような極端にスコアが低い状態、または逆に距離の遠いカードどうしが並べられた極端にスコアが高い状態、というのはカードの入れ替えに弱く、カードの入れ替えでスコアが大きく変化します。逆によく混ざっているときは、(もうまざっているんだから)スコアはそれほど変化しないはずです。
よく混ざったカードのスコアがどれくらいになるかはシミュレーションで求めることにする。
・山の並べ替えの操作は、2枚のカード置換の組み合わせに帰着される。(「対称群」の特徴)
・最小スコアである51点の山から始め(前述)、ランダムなカードを2枚選び入れ替えるという操作を繰り返す。

図1はそのようなシミュレーション試行の最初の1000回のスコア推移を示したもの。最初の数10回の置換で急激にスコアが悪化し、ある程度で落ち着くが、その後も多少の上下ふらつきがある。ここでは落ち着いた後の部分の統計的性質を調べる。立ち上がりについては後ほど評価する。
上記の1000回置換の後、ここを新たなスタートとして100万回置換を行った。図2は100万回のスコア推移、図3はその最後の1000回分を拡大したもの。やはりスコア250程度で上下にふらつく状態が平衡状態と言える。


図4はスコア分布のヒストグラムで綺麗な正規分布状の形をしている。実際、歪度-0.065 (正規分布なら0)、尖度2.944(正規分布なら3)と極めて正規分布に近い。
・スコア平均mは262.9。組あたりの平均距離は5.2程になる計算。意外に近いと感じるか?
・標準偏差σは19.43。

正規分布の性質から
・スコアが1σの範囲(m−σ, m+σ)=(243,282)の間に落ちる確率は68%、
・2σの範囲(m−2σ, m+2σ)=(224,302)の間に落ちる確率は95%。
以上から「山」について混ざっているかを判別する「レシピ」として
・カードの山を全部見てスコアを計算する。
・スコアが224~302の範囲に入っていれば、およそ「混ざっている」
と判じてよい
3) 何回くらい混ぜると「よく混ざる」か?
今度は前半部で、整然としたカードを混ぜていくと、スコアが悪化していく様子に着目する。
図5は最初にスコア51の状態から開始しランダムな2枚置換を行った時のスコア推移である。最初の100置換分について50ランのシミュレーション試行にを重ねて描画したものである。これをみると、45組程度置換をすればほぼ2σ圏内(水色)に入ることがわかる。

ところで、普段カードを混ぜる(切る)時、ちまちまと2枚ずつ置換したりなど、まどろっこしくてやっていられない。
実際の現場ではriffleという手法でカード・シャッフルを行っている。山を2つに分けて、片方を相手に差し込み、山として整え直す「あの技」である。このriffleを行うとどう混ざるか?
山を半分(カード26枚x2)に分割し、交互に重ねる、つまり結果として1枚目, 27枚目, 2, 28, ...., 26, 52枚目というように混ぜる方法を試してみる。
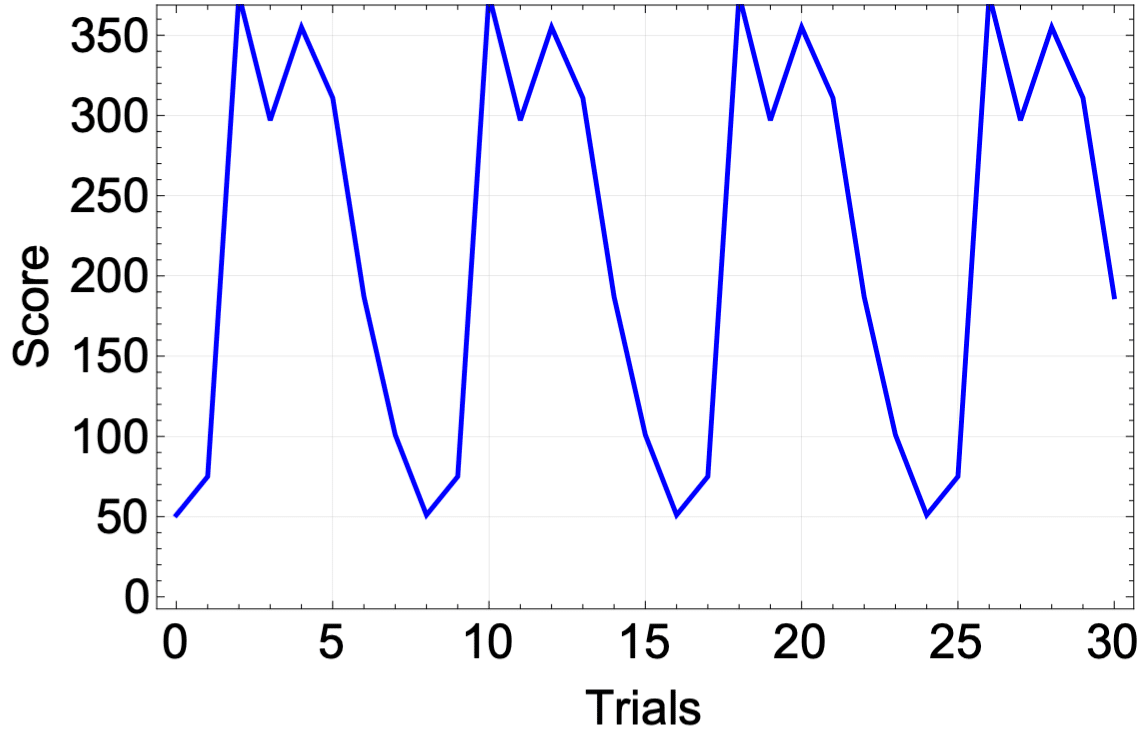
結果を図6に示す。横軸はriffleの回数だが、8回目に元のスコア51に戻り、その後もスコアを繰り返してしまう!これはこのような確定的な順列操作が持つ特徴で、決まった操作を繰り返していると必ずいつかは初期状態に戻ってしまうのである。(「何回で戻るか」を群論では「位数」と言う)
たとえばルービックキューブでも同じ動作を繰り返していると、いったんは色が混ざるがいつかは戻ってきてしまうのだが、これは全く不思議なことではなく、置換操作の自然な性質である。
これを防ぐにはある程度のランダムな操作が必要となる。そこで、
より一般化したriffleを定義して、ランダム性を加味したriffleを行い、スコアを評価する。
n-riffle:
カードが1, 2, 3, ...., 52と並んでいる時、最初の1からnまでをn+1から52までの中央に差し込む(図7)
1, 2, ..., n-1, n
n+1, n+2, ..., 26, 27, 28, ...., n+25, n+26, n+27, n+28, ...., 52

さらに、riffleする度に差し込むカードを「上から取るか」「下から取るか」を交互にすることにした。これは上記n-riffleの後にカードを逆転して並べることに相当する。つまり
52, 51, ..., n+26, n, n+25, n-1, ..., 28, 2, 27, 1, 26, ..., n+2, n+1
この逆転操作の理由は、図示したやり方を繰り返していると、黄色い部分はなかなか混ぜ合わされず、いつまで経ってもそのままであるためである。
前述の通り、このn-riffleでもnを固定にしてしまうと結果が乱雑にならないので、nは毎回乱数で決めることにする。nが小さすぎても大きすぎても混ざりが悪いようなので、良い塩梅とされる52/3~17程度で上下に振ることにして、n=14~20の乱数を使用した。
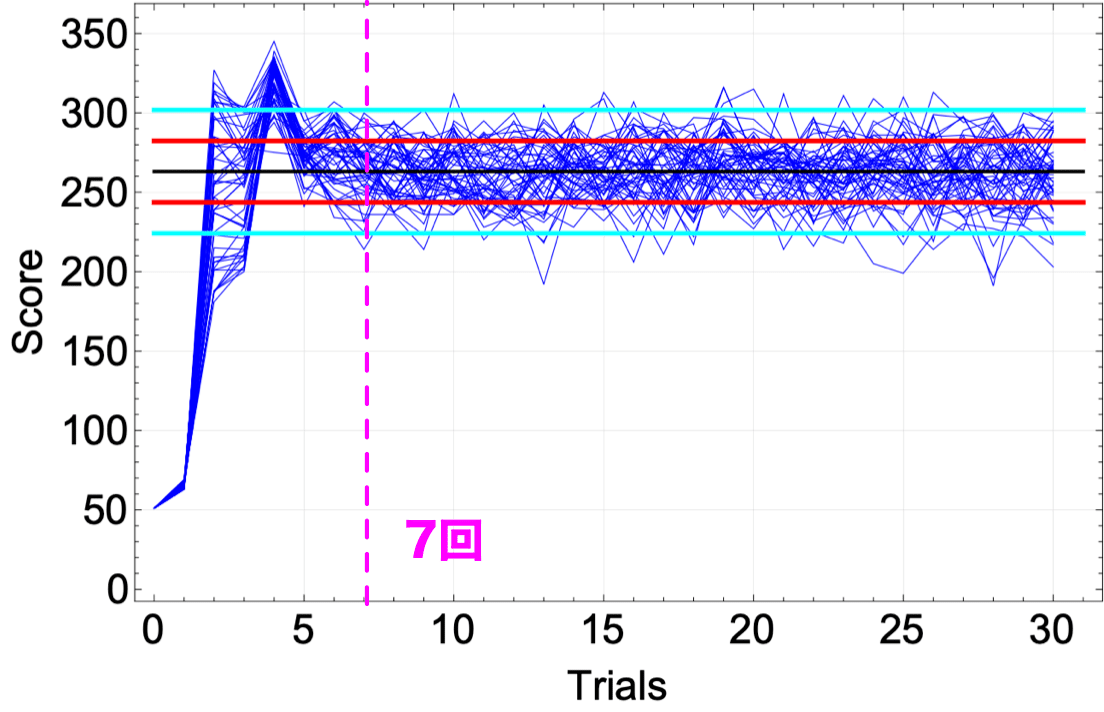
50回のシミュレーション試行の結果を図8に示す。横軸はriffleの回数で巷で言われているように7回ほどriffleすることででほぼ混ざった状態になると言えるだろう。心配だったらもう1回混ぜれば完全にOKだろう。
1/3程度をカード中央に差し込むようにシャッフルする
巷で言われているように7回ほどでよく混ざる
ただし、差し込み枚数は毎回少し変える
