一般化google卵問題

Yさんがどこかから問題を拾ってきた。

100階建てビルから落として卵の強度を調べる。
ある階よりも高くから落とすと割れてしまう。
卵の強度は共通で、2つまでは割ってもよいとする。
どのように調べれば最大検査回数を少なく抑えられるか。
その検査回数は何回か。

どうもネットでは有名なgoogleの入社試験の一部らしい。この問題の答え自体は「14回」で、検索すると解法付きで結構出てくる。たとえば

とか、他にもいろいろ。この問題自体は数学のパズルと言えるが、現実に電子デバイスのテストなんかではあり得る話である。例えば

ある素子に0V~100Vを印加して、どの電圧まで壊れないか1Vの精度で知りたい。手持ちの素子は2個しかない。テストごとに結構時間がかかる。なんとかその2個でナルハヤで終わらせて！

とか。

さて、ここでTさんが

「n階建てビルでm個の卵を使えるときは何回で検査可能になるか？」

と自然至極な拡張を持ち出す。OK, challenge accepted。一般化してみようじゃないか。

一般化卵落下問題

定式化を少し工夫する。出題の「n階建てビルでm個の卵を使えるときは何回で検査可能か？」ではなく、

m個の卵をk回使って調べるとして、何階建ての建物までなら卵の割れる階を特定できるか

と考える。この「何階建てまでなら」を関数F_m(k)と定義する。

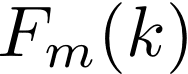
1) 卵が1個の時

下から1階ずつ調べてどこで割れるか見るしかないので、

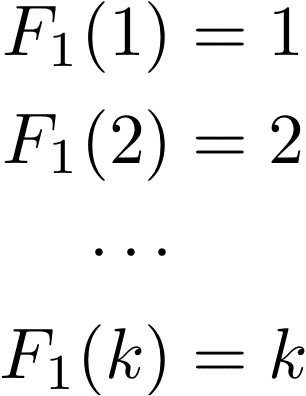
2) 卵が2個の時

k=1: 1回しか試せないなら卵1個も2個も同じ

k=2以上:
とある階から、今いる階にジャンプしてきた。
・ここで成功したら残り卵2個でk-1回検査可能。つまりF_2(k-1)階調べられる。
・ここで失敗だったらF_1(k-1)階調べられるから、漏れなく調べるには、前いた階はF_1(k-1)+1だけ下。（下図参照）

つまり、漸化式で表現すると

で、Mathemaicaで計算すると

はい、k=14ではじめて100を越えるので、卵2個なら100階のビルでもっとも効率良くやれば、14回以内に卵が割れる階を特定できることになる。

3) 卵がm個の時

m=2の時と同じように考える。

k<mのとき:
卵の個数より少ない階数しか試せないなら、試行回数は階数と同じになる。

k>=m:
とある階から、今いる階にジャンプしてきた。
・ここで成功したら残り卵m個でk-1回検査可能。つまりF_m(k-1)階調べられる。
・ここで失敗だったらF_m-1(k-1)階調べられるから、漏れなく調べるには、前いた階はF_m-1(k-1)+1だけ下。
つまり漸化式は

Mathematicaで計算させると

となる。これで一応、一般の場合の計算は出来るようになった。

もう少し考える

もっと解がエレガントにならないかもう少し頭を使って考える。
F_2(k)はその計算の経緯から言って、素直にsumで書けて

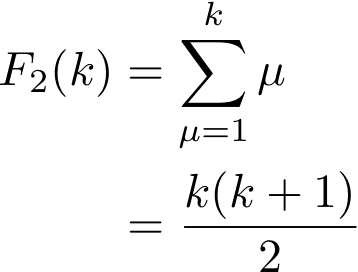
おお、なんかキレイ。じゃあF_3(k)はどうか？F_3(k)の漸化式を睨むと

なので、F_3(k)はF_2(k)の総和で書けそうだ。

うーん、F_3(k)の一般式はキレイにならない。ではF_3(k)-F_2(k)は？

おおお！これは綺麗だ！そうだよく考えると　k(k+1)/2 = k (k-1)/2 + k　だから、

summationを使って、

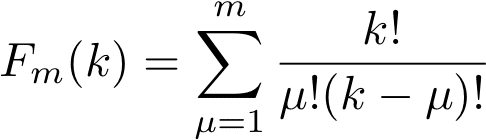
しかも、この中身は二項係数だから

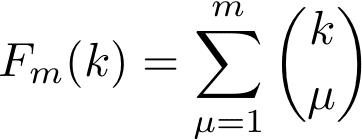
となる。おおお！ただし、これは現時点ではあくまで予想である。

帰納的証明

では証明を

・m=1のとき

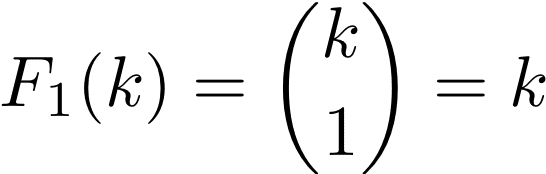
・一般のmで

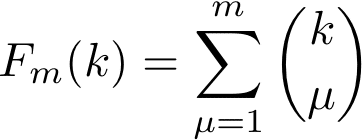
ならば

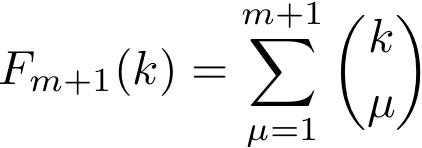
となる(*)ことを示す。漸化式から

ここで以下の全てを準備して

これらを足し上げて、F_m(0)=0に留意すると

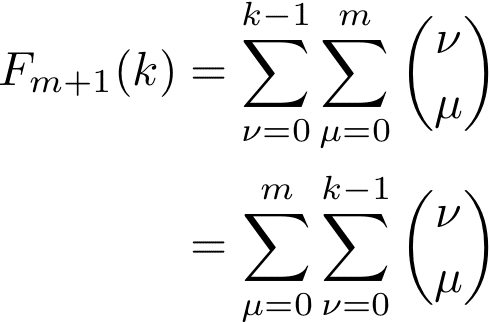
ここで

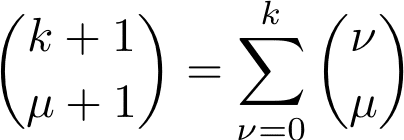
を使用すると(くわしくは補遺で)

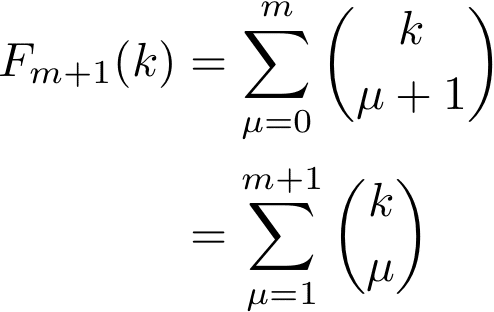
よって(*)が証明された。

巨人の肩

じゃーん

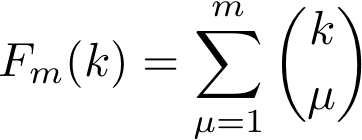
や、これは美しいじゃないか。卵落とし問題が二項係数の総和で書き表せるなんて！

それで二項係数のWikipedia読んでたら

二項係数 - Wikipedia

式(9)のすぐ下の記述に、まさにこの式が出てきて、

（この数式）に対する閉じた式は（超幾何函数を用いなければ）ない[8]が

フムフム、超幾何函数を使わなければこれ以上直接的な式にはならないと。それでこの文献[8]をみると

8. Boardman, Michael (2004), “The Egg-drop numbers”, Mathematics Magazine 77 (5): 368–372, JSTOR 3219201, MR1573776

ホワァッ!? Egg-drop numbers!? ぎゃぁー！私はこの文献にアクセスできるので恐る恐る読んでみると、まさにこの問題とおなじアプローチおなじ答え。

やっぱ大抵の問題は既に踏破されてる。巨人の肩の上に立つのは大変デス。笑

余談

最近読んでいた大栗博司先生の「探求する精神 職業としての基礎科学」(幻冬舎新書)によると

探究する精神 職業としての基礎科学 (幻冬舎新書)

「超弦理論に関する博士論文で計算した係数列が、ラマヌジャンのテータ関数の級数であると20年後に気づいた」って書いてあって、さすが本物は二項係数ごときで喜んでいるようなsmall fishとは違うな、と思った。

補遺

二項係数のパスカルの法則

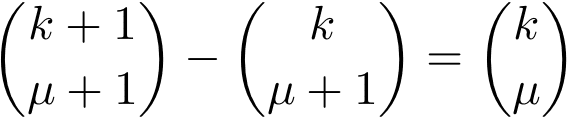
再帰的に使用すると

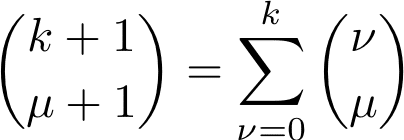
を得る。図解的にこれを理解しようとすれば、半自明である。下図の赤長丸の和が赤丸と同じになる（青も同様）、と理解できる。

#卵落下問題 #卵問題 #数学 #数学パズル #パズル #論理パズル #google入社試験 #入社試験 #二項係数