
とある落ちゲーを自動で解かせる話 その1
Pentasというゲームに10年ぶりくらいにハマってしまった。たしか初期のKindle Fireで遊べたのであるが、最新のAndroid・iOSでも動くのを発見し、またやってしまったのが運の尽き。
Pentasは一言で言うと「ムカつく」落ちゲーである。8x8の盤面を指定のピースの形に消していって、空行を作るとその行が消滅し、上から一段落ちてくるというものだ。ピースはペントミノ、つまり5ブロックでできていて、当然ながらランダムに指定され、いまやっつけるべきピース(現ピース)と、もう一つ(次ピース)まで開示されている。例えば下図の例は、風前の灯火の盤面であるが、1行目か3行目に水色のピースを横に当てれば一行消えるので、なんとか生き残れると言う状態である。どちらが良手か?多分3行目を消した方が上3行の手幅が広がるので良いと思うがどうか。

スコアシステムもシブめで、1ターンでブロック分の5点加算、1行消すと追加で8点加算されるだけである。複数行同時消しボーナスはない。ちなみにリアルタイムゲームではないので、一手打つのに何時間使っても構わない。実に地味でカタルシスも少ない。どんなに綺麗に消し上げていっても、突然「+」ピースの連続でめちゃめちゃにされたり、待ちがツモらずに終わることも多く、フラストレーションが溜まりまくる。で、また次のプレイを始めてしまうのであるが…
(追記:ゲロっ!なんと最近のバージョンでは複数行消しボーナスがあるらしい。10年前はなかったはず。現在のスコアリングでは1行消しで+8、2行消しで+25、以降+70, +190, +450となっているようだ。当方調べ)
私が200回くらいプレイして平均が700点程度であった。余りにすぐ詰まって頭にきたんで、盤面をシミュレートするコードをPythonで書き、アルゴリズムで自動プレイさせることにした。ゲームで時間を溶かすのなら、コーディングのトレーニングにした方がまだ有意義だろうという判断である。
コーディングの前に
コーディングするに当たり、まじまじとゲームのルールを考察してみた。思うようにならない理由の一端はピース数の多さが原因である。ペントミノは全部で12種。テトリスで使われているテトロミノが5種(パリティを考慮すると7種)であるのに比べると格段に多い。
つまり、盤面を調整してある特定のピースのツモを期待しても当たる確率はかなり低い。そしてボーナスもないからそうする理由はない。であるから、戦略としては不確実な未来に期待せず、開示情報からのみで割り出される現世御利益を重視したアルゴリズムで手を打っていけばそこそこ良いだろう。巨大な探索システムを作らなくて済みそうだという点もコード化してみようと思った経緯のひとつである。
クラスとデータ構造について考える
コーディングの前にいくつか必要な機能について考えてみた。
・ゲームを構成する要素は、盤面、現ピース、次ピース、スコア。これにターン番号、このターンで選んだ手、それにスコアに準じた情報として何ライン消したかも記録することにする。
これらはdictionaryとしてまとめた上で、ターンの記録としてリストに積み上げていくことにする。ゲームが終われば、これをログとして保存して、成績の良い物はあとで棋譜のように眺めることができるようにする。
・ピースについて。
ピースの情報を数値情報で入力するのはめんどくさいので、可読性の高い状態で与えておき、クラスが読み込まれたときにクラス関数で内部情報へと変換しておくことにする。
・なんらかの盤面表示機能。
・各種ユーティリティ機能。
初期ゲームデータ作成、可能手のチェック、ピースの適用、空行発生処理、など
・盤面サイズはクラス変数として定義し、別サイズの盤面でも動くようにコードを書く。
これらをPentasクラスとして定義し、ゲームドライバーコードから利用する。
コードについて
開発はPython 3.8.5でおこなって、コードは以下のgithubで公開している。
pentas.py: Pentas Classの定義
pentas_auto_play.py: ゲームドライバー。これを実行してゲームさせる
game_analysis.ipynb: ゲームのログを解析するpython notebook
Pentas Class: 盤面について
盤面サイズはクラス変数として定義し、別サイズの盤面でも動くようにコードを書く。
boardsize_v=8
boardsize_h=8
boardsize=[boardsize_v, boardsize_h]
このとき盤面自体はサイズv*hの行列にせず、v*x要素の1次元のnumpy arrayとする。1次元にした方がピースの消去処理がしやすいからである。すなわち、8x8盤面の場合、盤面の左上から
0 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15
16 ...と番号を振っていく。
Pentas Class: データ構造
init_new_game で新しいプレイを作成する。初期ターンは
turns=[{
'turn': 0,
'board': np.array([1]*Pentas.boardsize_v*Pentas.boardsize_h),
'score': 0,
'lines': 0,
'current_piece': Pentas.pick_piece(),
'next_piece': Pentas.pick_piece()
}]と定義され、これに適用手をturns[turn]["placement"]として加えてターンが完了する。結果のボードは次のターンの盤面に記録される。
Pentas Class: ピースについて
ピースの元となるものは、リストとして以下のように定義して与える。例えば
pieces= [
[
"ooooo" #I
],
[
"oooo", #L
"oxxx"
],で、最終的にこれらを
[0,1,2,3,4]
[0,1,2,3,8]などに変換したい。ただし、回転や反転も扱うので、最初のIピースであれば
[0,8,16,24,32]も生成する。
そこでまず、この"o"と"x"のリストを0,1でできたリストに変換し(__convert_piece_in_array関数)、これに対して変換操作を行いピースバリエーションを作成する(__piece_variations関数)。念のため左右反転・上下反転・45度鏡像(転置)・CW回転・CCW回転の関数を定義したが、実際には転置とCW回転だけで可能な8種類全てが網羅される。
この反転操作をした場合、対称性によっては既に存在する形と重複する。例えば「+」はどう変換してもオリジナルと同じになる。初めはunique関数か何かあるかと思ったが、存在しないようなので、新しいピースバリエーションを登録したいときに既存かどうかを判定知る関数として__array_is_in関数を用意した。
最後に、できあがったピースバリエーションをブロック位置を表す数値列に変換していく(__convert_piece_variation_to_poslist)。
Pentas Class: 盤面表示について
display_board関数からプライベートメソッドを呼び出して表示文字列を構築する。地道な作業なので全ては記述はしないが、
__display_board_preparationで盤面を作成
__display_add_pieceで盤面の右にピースディスプレイを追加
__display_add_statsで盤面の右下方にスコアその他を追加
placement指定がある場合、ピースがどこに置かれるかを#でプレビューする(__display_piece_preview)
表示例はこんな感じになる
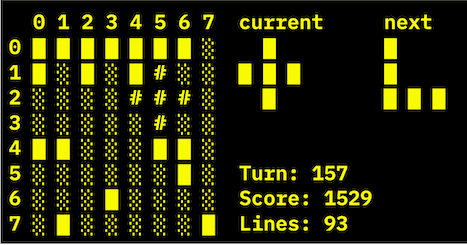
この辺はコードがdumbですが、これはまあ良いでしょう。
Pentas Class: 各種盤面ユーティリティ
derive_possible_moves関数は与えられたピース種について、各バリエーション毎について総当たりし、ブロックを消せる場所をすべて探索する。
まず、スキャン範囲はピースの縦横サイズを考慮して制限する。例えば下図のLピースを横にしたものは[0,1,2,3,8]であり、ピースの0を基準に考えると
盤面の青で塗られた部分までは探索可能である。

つぎに、探索位置(オフセット)が決まったらボードのオフセットを基準にして、ピースの位置数値を足したブロックの値を読む。上の例でオフセット16で探索すると16, 17, 18, 19, 24の盤面を読むことになる。実際にはいちいちfor loopでは読まず、numpy arrayのファンシーインデックスを利用して一気に値を取得する。(これは盤面を1次元にする御利益)
このとき取得した値に"0"がなければこの配置は「可能」なので、np.prodで要素の乗算を取り判定する。判定がOKであれば、possible_moveにストックして返す。可能手はバリエーション毎にリストにして返す。あるバリエーションに対し可能手がない場合、空リスト[]が返される。つまり可能手のどの要素を見ているかとバリエーションの種類が対応していることに注意。
apply_piece関数ではあるピースを与えられた手で適用したときに盤面がどうなるかを処理する。ここでは手が適正かどうかの判定はしない。
check_if_line_cleared関数では1行が空になったかを判定し、もしそうならそれより上の行を下げてトップに新たなブロックを置く作業をする。この関数のコードはdumbなので、改善できそう。
calc_surface_area関数については後ほど既述する。
Pentas Class: ゲームユーティリティ
init_new_game関数は既に記述済。
execute_a_turn関数は実際にピースを適用し、空行を消し、それらのスコアを算定したうえで、適用手の記録、次手のレコードの作成を行う。
最善手アルゴリズムについて
まずピース配置は総当たり。探索パス1では、現ピースを置ける位置と向きを総当たりする。探索パス2ではパス1の可能手それぞれにおいて次ピースを総当たりする。
その全ての可能手のリストからコスト関数を最小にする手を最善手としてピックアップする。
コスト関数であるが、冒頭で述べたように開示情報から現世御利益を重視するのが戦略である。そこで思案したが、だいたいブロックがバラバラになると詰むので、盤面の表面積(海岸線の長さ、というべきか)をコスト関数とすることにした。盤面の左・右・下はブロックが無く、上にはブロックがあるとし、ブロックの「島」と「海」の境界の個数を足し上げた物を「表面積」とした。(下図参照)
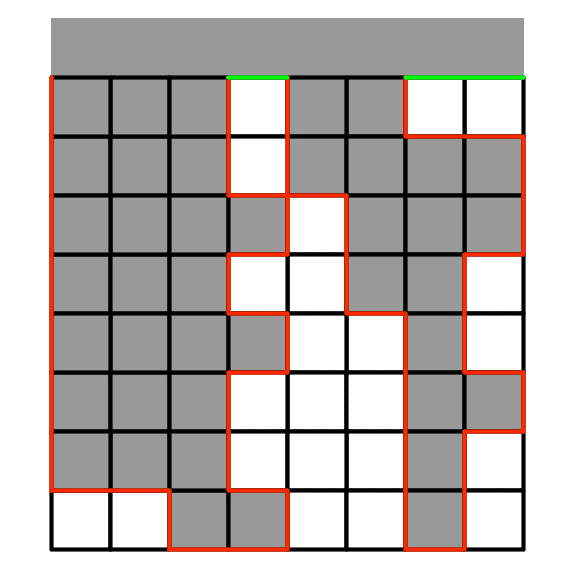
表面積だけを最小にする手を選ばせるとかなりヘンテコな手を選んでしまうので、1行消せる毎にコスト関数から行クリアボーナスとして、1行毎に表面積から3を差し引くことにした。この「3」の根拠は次投稿で既述する。このボーナス以上に複数行消しを優先する要素は入れていない。
表面積の計算について、最初は行ごと・列ごとに計算していた。たとえ
[0,1,0,0,1,1,0,1]と言う行があるとき、盤面の左右はブロックがないので、左右に0を追加して
[0,0,1,0,0,1,1,0,1,0]とし、この中で0->1/1->0の遷移が幾つあるかを数える。数え上げは差分を取って行う。すなわち[0,0,1,0,0,1,1,0,1,0]と一個左ずらしの[0,1,0,0,1,1,0,1,0,0]の要素毎の差を計算し
[0,0,1,0,0,1,1,0,1,0]-[0,1,0,0,1,1,0,1,0,0] = [0,−1,1,0,-1,0,1,-1,1,0]要素の絶対値[0,1,1,0,1,0,1,1,1,0]を足し上げた6が遷移の個数になる。
これを全行について行うと横の表面積が得られる。
縦の表面積については行列の転置を取り、同じ操作を行う。ただし、前方には0の代わりに1を追加する。
処理的にはこれでよいが、コードの処理速度プロファイルを取ったところ、この表面積計算が大半の時間を取っていることが判明したため、実際のコードでは「前後に追加」を行列で処理し、差分も行列で取るようにした。この結果、この関数の処理自体は12倍の高速化、全体では4倍の高速化が達成できた。
ゲームドライバーについて
ゲームドライバー(pentas_auto_play.py)では上記アルゴリズムに従った最善手探索と適用を行い、最終的に手詰まり(可能手が存在しない)ところまで打ち続ける。
同一コストの最善手が複数ある場合、最後の物すなわち一番右下のものを採用するようにした。これは同じコストであれば下の方から取っていった方が直観的には有利な気がするからである。
最善手が存在しなくなったとき、それはあと一手しか打てない(「必死」)ことを意味するので、なげやりに最後に見つかった手を採用している(おっとここはなるべくスコアが最大になる手を選ぶべきで、未修正のバグだ。)
打つ手が全くなくなったら、ゲーム終了としてゲームの経過時間・1ターンの探索にかかった平均時間を表示し、棋譜をpickleを使って日付つきのログファイルに保存し、次のゲームを再始動する。
それではいよいよ次稿で、見せて貰おうか、アルゴリズムの性能とやらを。
