
世界の法則を知るために-微分・積分とは?積分の応用例(4)
半径が$${ r}$$の球の体積を$${ V}$$、表面積を$${ S}$$とし、定積分を使った回転体の体積の求め方を使うと球の体積の公式、
$${ \displaystyle V=\dfrac{4}{3}\pi r^3}$$
を求めることができます。
また球の表面積の公式は、
$${ S=4 \pi r^2}$$
となります。
今回は、最終目標としていた球の表面積の公式を求めます。
この公式は、微分を使って求めることができます。
球の体積と同じように、球の表面積の公式は中1で習いますが、公式を覚えるだけでなぜ公式のようになるかはわからないと思います。
今回の内容がわかれば、球の表面積がなぜ公式のようになるかわかります。
2つの円の面積
球の表面積の公式を求めるために使う考え方を、球より簡単な円を使って解説します。
次の、

のように、黒線で表した半径$${ r}$$の円、赤線で表した黒線の円より半径が$${ \Delta r}$$長い円を考えます。
以下では、黒線で表した円を黒い円、赤線で表した円を赤い円と言います。
また青色部分のように、赤い円と黒い円の面積の差を$${ \Delta S}$$とします。
ここで$${ \Delta r}$$が小さいとき、青色部分である$${ \Delta S}$$を求めることを考えます。
このことは、球の表面積の公式を求めるために使います。
この青色部分を、

のように赤い点線で切って広げると、

のような台形となります。
このとき黒線の長さは黒い円の円周の長さ、赤線の長さは赤い円の円周の長さとなります。
ここでこの台形は、$${ \Delta r}$$が小さいときを考えているので、

のように黒線と赤線がほとんど同じとなります。
つまり、黒線である黒い円の円周の長さと赤線である赤い円の円周の長さがほとんど同じになります。
このとき、長方形とほとんど同じと考えることができます。
このように長方形と考えると、黒線である黒い円の円周の長さを$${ l}$$とすると、
$${ \Delta S \fallingdotseq l \Delta r }$$
となります。
ここで$${ \Delta r}$$が小さいとき、長方形と同じではなくほとんど同じとなるため$${\fallingdotseq}$$を使っています。
球の表面積
ここでは、球の表面積について考えてみましょう。
半径が$${ r}$$の球の表面積を$${ S}$$、体積を$${ V}$$とすると公式から、
$${\displaystyle S= 4 \pi r^2,V= \dfrac{4}{3}\pi r^3}$$
となります。
この表面積である$${ S}$$は、体積である$${ V}$$から求めることができます。
次の、

のように、黒線で表した半径$${ r}$$の球の断面図、赤線で表した黒線の球より半径が$${ \Delta r}$$長い球の断面図を考えます。
以下では、黒線で表した球を黒い球、赤線で表した球を赤い球と言います。
また青色部分のように、赤い球と黒い球の体積の差を$${ \Delta V}$$とします。
このとき、$${ \Delta r}$$が小さい場合の$${ \Delta V}$$を求めることを考えてみましょう。
この場合、2つの円の面積のときと同じように考えることができます。
この青色部分を、
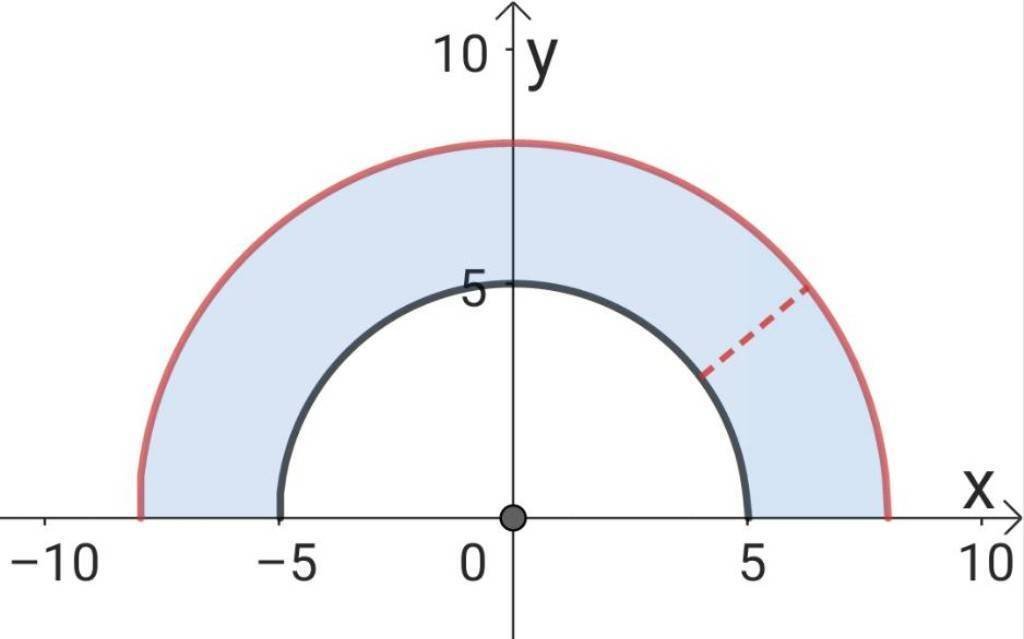
のように赤い点線で切って広げ、$${ \Delta r}$$が小さいときを考えると、黒線と赤線がほとんど同じとなります。
つまり、黒線である黒い球の表面積と赤線である赤い球の表面積がほとんど同じになります。
このとき青色部分は、
底面積が黒い球の表面積$${ S}$$、高さが$${ \Delta r}$$の立体
と考えることができます。
このように考えると、
$${ \Delta V \fallingdotseq S \Delta r }$$
となります。
ここで$${ \Delta r}$$が小さいとき、同じではなくほとんど同じとなるため$${\fallingdotseq}$$を使っています。
この式で両辺を$${ \Delta r}$$で割ると、
$${\displaystyle S \fallingdotseq \dfrac{\Delta V}{\Delta r}}$$
となります。
ここで$${ \Delta r}$$を、
$${ 0}$$に限りなく近づけたとき
を考えると、
$${\displaystyle S = \dfrac{dV}{dr}}$$
のように、ほとんど同じではなく同じとなるので$${ =}$$となり、$${ \Delta}$$を$${ d}$$と置き換えることができます。
この式から球の表面積である$${ S}$$は、
球の体積である$${ V}$$を、半径である$${ r}$$で微分する
と求めることができます。
このことから、
$${\displaystyle V= \dfrac{4}{3}\pi r^3}$$
なので、$${ \pi}$$は定数であることに注意して計算すると、
$${\displaystyle S = \dfrac{dV}{dr}=\dfrac{d}{dr} \left( \dfrac{4}{3}\pi r^3 \right)}$$
$${\displaystyle =3×\dfrac{4}{3}\pi r^{3-1}=4\pi r^2}$$
となります。
この式から球の表面積は、
$${\displaystyle S =4\pi r^2}$$
となり、球の表面積の公式を求めることができます。
まとめ
今回は、半径が$${ r}$$の球の体積である$${ V}$$を、$${ r}$$で微分すると表面積である$${ S}$$が、
$${\displaystyle S = \dfrac{dV}{dr}=\dfrac{d}{dr} \left( \dfrac{4}{3}\pi r^3 \right)=4\pi r^2}$$
のように求めることができることについて書きました。
中学生は、球の体積と表面積の公式は必ず覚えたほうが良いと思います。
しかし、球の体積を微分すると球の表面積になることを覚えている、微分の計算方法がわかっているとなれば、球の表面積を忘れたときに求めることができるため、今回の内容を知っていて損はないと思います。
今回で、積分の応用例は終わりとなります。
次回は、微分と積分の両方を使う例として、微分方程式というものを扱います。
この記事が気に入ったらサポートをしてみませんか?
