
【Shadowverse】マゼルベイン軸における、採用カード種類数の実験と考察
概要
「唯我の絶傑・マゼルベイン」は「唯我の絶傑・マゼルベイン」以外のカードは全て1枚ずつのデッキを構築しなければならなかったが、「絶大の唯我・マゼルベイン」はデッキ内の残りカード種類数が20種類以上であればいい。そのため、デッキ構築の自由度が上がり、何種類かのカードを複数枚積むことができるようになった。そこで、複数枚採用が何種類までなら許容できるのか、構築段階で少なくともデッキ内に何種類のカードを積むべきなのか、といった考察を行った。
実験内容について、あるデッキ構成において、デッキをシャッフルしてマリガンするところ ~ カードを引き続けてデッキ内のカード種類数が20種類未満になるまでを「1回の試行」とし、この試行を100万回行う。この一連の流れを以下の条件下で構築可能なデッキ構成全てに対して行う。
・デッキ枚数40枚
・「絶大の唯我・マゼルベイン」3枚
・構築段階でのデッキ内カード種類数が20種類以上
これらの試行によって集めたデータについて、各デッキ構成ごとに箱ひげ図を表示し、それらを比較することで前述した考察を行う。
実験結果として、前述の条件下で構築可能なデッキ構成は100個見つかった。初期手札3枚 + 先攻6ターン目までのターン開始時ドローの6枚 = 合計9枚のカードを引いた時点において、ほとんどの試合でデッキ内の残りのカード種類数がまだ20種類以上であることを理想とし、稀にしか発生していない事例である外れ値を考慮しない場合、「絶大の唯我・マゼルベイン」以外の37枚について、3枚採用3種類 2枚採用5種類 1枚採用18種類、3枚採用4種類 2枚採用3種類 1枚採用19種類など、少なくとも26種類以上あれば達成しやすいことが箱ひげ図より見て取れる。
つまり、「絶大の唯我・マゼルベイン」も含めると「27種類以上のカードで40枚のデッキを構築すればいい」ということである。
外れ値も考慮したい、後攻時やドロソなどを使って6ターン目までに10枚以上カードを引いた場合でも、ほとんどの試合で20種類以上を保っていたいなど、より確実に「絶大の唯我・マゼルベイン」の条件を達成したい場合はデッキ内の総カード種類数を27種類よりも更に増やすことを検討してもいい。
しかし、デッキ内の総カード種類数を増やすことは複数枚採用のカード種類数を減らすことと同義であり、試合の再現性を損ないかねない。
これらを加味したうえで、今回の実験結果を基にデッキの最適化を行うことが重要であると私は考える。
以下、本文です。
1. はじめに
読者の皆様、こんにちは。月山です。
今回は先日実装された「絶大の唯我・マゼルベイン」についての考察を行います。

リメイク前である「唯我の絶傑・マゼルベイン」では、「唯我の絶傑・マゼルベイン」以外のカードは全て1枚ずつのハイランダー構成にしなければなりませんでした。
それに対して、リメイク後の「絶大の唯我・マゼルベイン」は、使った時点でのデッキ内の残りカード種類数が20種類以上であれば追加効果を発揮できます。そのため、デッキ構築の自由度が上がり、何種類かのカードを複数枚積むことができるようになりました。例えば、ドラゴンクラスで構築する場合に「竜の託宣」や「イグニスドラゴン」といったPP加速札を複数枚積むことで、序盤のPP加速を安定させながらマゼルベイン早期着地を狙うこともできます。
しかし、複数枚積むカードの種類が増やせば増やすほど、マゼルベインを出した段階でデッキ内の残りカード種類数が20種類を下回ってしまう可能性は高くなります。
つまり、試合の再現性を保ちながら20種類以上を保ちやすいようにするには、複数枚積むカードの種類数を最適化する必要があります。
そこで、疑似的に再現したデッキで実験を行い、複数枚採用が何種類までなら許容できるのか、構築段階で少なくともデッキ内に何種類のカードを積むべきなのか、といったデッキの最適化についての考察を行いました。
2. 実験の内容
実験内容を簡潔に説明します。
あるデッキ構成において、デッキをシャッフルしてマリガンするところ ~ カードを引き続けてデッキ内のカード種類数が20種類未満になるまでを「1回の試行」とします。つまり、マゼルベインの追加効果の条件を達成している間のみカードを引き続けるということです。この試行を100万回行います。
この一連の流れを以下の条件下で構築可能なデッキ構成全てに対して行います。
・デッキ枚数40枚
・「絶大の唯我・マゼルベイン」3枚
・構築段階でのデッキ内カード種類数が20種類以上
最終的に、これらの試行によって集めたデータを各デッキ構成ごとに箱ひげ図として表示し、それらを比較することで前述した考察を行います。
また、今回の実験では、実際にゲーム内で試合を行って集計したのではなく、デッキ構成を数値で疑似的に再現し、それをプログラム上で回すことによって集計しています。
実際に使用したプログラムをGoogle colabで実行できるようにしたので、興味のある方はこちらよりお試しください。
※補足1
「絶大の唯我・マゼルベイン」の採用枚数について、当たり前のことではありますが、採用枚数を増やせば増やすほど「絶大の唯我・マゼルベイン」を引く確率は高くなります。そのため、今回は最大枚数である3枚に設定して実験しました。
上記にリンクを貼ったGoogle colab内のプログラムでは、「絶大の唯我・マゼルベイン」の枚数やデッキ枚数などを変更して実験することも可能です。
※補足2
今回の実験方法以外の方法として、シャッフル後のデッキ内のカードの順列を全て列挙する方法が考えられます。しかし、この方法は用いませんでした。
理由として、この方法で40枚のデッキ構成全てに対して実験する場合、列挙する量が最も少ない 3枚 × 13種類 + 1枚 × 1種類 = 計40枚のデッキ構成だけでも 6.2471051e37 通り (※比較例として、1e12 通り = 1 × 10 ^ 12 = 1兆通り) という途方もない量を考慮する必要があります。これを構築可能なデッキ構成全てに対して行うのは、少なくとも私の手元の環境では現実的ではありませんでした。
今回の実験方法では、この現実的ではない計算量を現実的な計算量に無理やり抑えています。つまり、実験結果は近似値です。
各デッキ構成ごとに10万回以上の試行を行えば、実験結果がきちんと収束することは確認済みですが、人によっては10万回以上の試行を行っても実行結果が多少変動する可能性があるのでご注意ください。(誤差レベルの変動ではありますが...)
3. 実験の結果・考察
前述の条件下で構築可能なデッキ構成は100個見つかりました。つまり、今回の実験全体での試行回数の総計は 100万回 × 100個 = 1億回です。
各デッキ構成についての実験結果を箱ひげ図にしたものを以下に示します。 (※箱ひげ図の見方についてはこちらよりご確認ください。)
横軸のx_x_xは「絶大の唯我・マゼルベイン」以外の37枚についての構成内容を表しています。例えば、2_6_19は3枚採用が2種類、2枚採用が6種類、1枚採用が19種類という意味です。つまり、この37枚だけで27種類、「絶大の唯我・マゼルベイン」を含めると28種類のカードで40枚のデッキを構成していることになります。
縦軸はデッキ内の残りカード種類数が20種類を保っていたドロー枚数を表しています。例えば、あるデータの縦軸が14枚の目盛の位置だった場合、そのデータの試行では15枚目をドローした段階でデッキ内の残りカード種類数が19種類になってしまったということを表しています。
また、デッキ内の残りカード種類数が20種類を保っていたドロー枚数について、箱の中央部にある橙色の線はその中央値、緑色の三角形は平均値を表しています。例えば、緑色の三角形が縦軸の12枚の目盛の位置に配置されているデッキ構成では、12枚ドローした時点ではまだ20種類以上を保てていた、という状況が平均的であることを表しています。中央値についても同様です。
また、図内の〇は外れ値です。データ数が少ない、稀にしか発生していない事例がこれにあたります。例えば、ドローしたカードが全て1枚採用のカードだった、複数枚採用したカードそれぞれについて1枚ずつデッキ内に残るようにドローしていた、などの事例です。

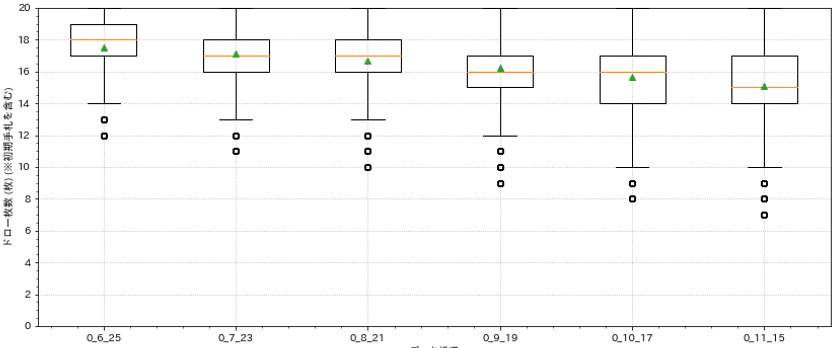















では、この結果を基に考察を行います。
例えば、初期手札3枚 + 先攻6ターン目までのターン開始時ドローの6枚 = 合計9枚のカードを引いた時点において、ほとんどの試合でデッキ内の残りのカード種類数がまだ20種類以上であることを理想とします。
前述した通り、外れ値は稀にしか発生していない事例であるため、これは今回は考慮しないこととします。つまり、箱ひげ図の最小値が9以上であれば理想の条件を満たしているということです。箱ひげ図の最小値が9のデッキ構成は以下の8通りです。
・0_12_13 ・1_9_16 ・1_10_14
・2_7_17 ・3_5_18 ・4_2_21
・4_3_19 ・5_0_22
これを見る限り、「絶大の唯我・マゼルベイン」以外の37枚を25 ~ 27種類のカードで構成することで理想の条件を満たせることがわかります。更に、試合の再現性を高めるために何種類かのカードは3枚採用することを考えると、少なくとも26種類以上あれば理想の条件を達成しやすいと解釈することができます。
つまり、上記の理想条件では、「絶大の唯我・マゼルベイン」も含めると「27種類以上のカードで40枚のデッキを構築すればいい」ということです。
また、0_12_13 と 5_0_22 を比較すると、箱ひげ図はほぼ同じであり、相違点は3枚採用のカード種類数とデッキ内の総カード種類数です。つまり、3枚採用のカード種類数を増やしたい場合はデッキ内の総カード種類数も増やす必要があると考えられます。
また、上記8通りのデッキ構成は四分位範囲がどれも13 ~ 16枚の間です。100万回の試行のうちの約半数がこの範囲に集中していることから、上記8通りのデッキ構成なら後攻1ターン目やドローソースを使った際の追加ドローは合計4枚までなら比較的許容しやすいと解釈できます。しかし、約25%の試合で4枚追加ドローしている間にデッキ内の残りカード種類数が20種類を下回ってしまっている点には注意が必要です。
外れ値を考慮したい、後攻1ターン目やドローソースなどを使って6ターン目までに10枚以上カードを引いた場合でも、ほとんどの試合で20種類以上を保っていたいなど、より確実に「絶大の唯我・マゼルベイン」の条件を達成したい場合は理想の条件を引き上げてもいいでしょう。しかし、その場合は複数枚採用のカード種類数を減らす必要があります。
例えば、先ほどは9枚のカードを引いた時点において、ほとんどの試合でデッキ内の残りのカード種類数がまだ20種類以上であることを理想としました。次はこれを12枚のカードを引いた時点に変更してみます。先ほど同様、外れ値については考慮しないことにします。つまり、箱ひげ図の最小値が12以上であれば理想の条件を満たしているということです。箱ひげ図の最小値が12のデッキ構成は以下の5通りです。
・0_9_19 ・1_7_20 ・2_5_21
・3_2_24 ・4_0_25
これを見る限り、「絶大の唯我・マゼルベイン」以外の37枚を28か29種類のカードで構成することで理想の条件を満たせることがわかります。「絶大の唯我・マゼルベイン」も含めると少なくとも29種類以上のカードが必要だということです。
先ほどよりもデッキ内の総カード種類数は増えていますが、複数枚採用のカード種類数は減っています。このことにより発生する問題として、試合の再現性を損なう可能性が挙げられます。
仮に、9枚ドロー時点で理想を達成しているデッキ構成の代表として 3_5_18 構成を、12枚ドロー時点で理想を達成しているデッキ構成の代表として 3_2_24 構成を選択し、ドラゴンクラスでそれぞれのデッキ構成のレシピを構築するとします。
「絶大の唯我・マゼルベイン」「竜の託宣」「イグニスドラゴン」をひとまず3積みした後、3_5_18 構成の場合は「独尊龍・スーロン」か「殺竜騎士・ロイ」の片方を3積み、もう片方を2積みにしてPP加速札を11枚にしつつ、「ブルータルドラゴニュート」「竜槍の戦士・ローウェン」「ブリザードハート・フィルレイン」「烈絶の侮蔑・ガルミーユ」「サタナエル」「双極の生命・フラム=グラス」などの強力なカードの中から4種類まで選んで2積みすることができます。「再臨する絶大」も2積みしやすいです。
それに対して、3_2_24 構成の場合は「独尊龍・スーロン」か「殺竜騎士・ロイ」の片方を3積みした時点で複数枚積めるカードは残り2種類になります。PP加速札を11枚にしたい場合、PP加速札以外は残り1種類しか2積みできません。
では、2枚採用と1枚採用ではどのような差があるのでしょうか。以下の2つのグラフをご覧ください。


Aというカードについて、上のグラフは2枚採用した場合の確率、下のグラフは1枚採用した場合の確率を示しています。横軸は初期手札を除いたドロー枚数を表しており、横軸 = 0 はマリガン終了時点での確率です。また、マリガンでのカードを返す枚数によっても確率は変動するため、想定しうる4パターンの返し方それぞれを色分けして表示しています。どの色がどのマリガンに対応しているのかはグラフの左上をご覧ください。
「絶大の唯我・マゼルベイン」は効果でデッキ内の全てのカードを1枚ずつにしてしまうため、効果発動後は特定のカードを引き込みづらくなるデメリットがあります。また、カードを複数枚採用する行為には、複数枚採用したカードを「絶大の唯我・マゼルベイン」を使うよりも前に予め手札に引き込んでおくことで、デメリットに振り回されることなくフィニッシュ札を安定して使える状況を整えやすくするという側面もあります。
そのため、「絶大の唯我・マゼルベイン」を使うターン、つまり、先ほどデッキ構成の理想条件として設定したドロー枚数の時点で引くことができる確率で比較することとします。
前述した通り、3_5_18 構成での理想条件は9枚ドロー時点です。この構成でAを2枚採用していたとしましょう。理想条件である9枚ドローの時点、つまり、上のグラフの横軸が6の位置での確率を参照します。上のグラフより、この条件での確率は 40.3846 ~ 49.7834% です。
では、この構成を 3_2_24 構成に変更し、その際にAを1枚採用に減らしたとしましょう。3_2_24 構成での理想条件は12枚ドロー時点です。つまり、下のグラフの横軸が9の位置での確率を参照します。下のグラフより、この条件での確率は 30.0000 ~ 35.6756% です。
つまり、Aを引く確率に 10 ~ 14% ほどの差が生じています。
このように、構成の変更に伴う採用枚数減らしはフィニッシュ札等を安定して確保しづらくする、つまり、試合の再現性を損なう主原因であると解釈することができます。また、外れ値を考慮する場合でも理想条件の変更が必要になるため、これと同様の問題が発生します。
これらの結果より、「デッキ内の残りカード種類数を20種類以上に保ちやすくする」と「試合の再現性」はトレードオフの関係であると解釈できます。
デッキ内カード種類数を増やしすぎたために試合の再現性が著しく低い、再現性を求めすぎたためにマゼルベインの効果が発動できない状況に陥りやすいなど、デッキの組み方を間違えると勝てないデッキを量産してしまいます。
マゼルベイン軸を構築するにあたり、
・「絶大の唯我・マゼルベイン」を使うまでに引きたいドロー枚数
・フィニッシュ札等の可能な限り毎試合使いたいカード (複数枚積みたいカード) の種類数
・下振れの許容範囲
といった条件を予め決めておき、今回の実験結果である箱ひげ図の中からその条件に合致するデッキ構成を見つけることがデッキの最適化に繋がると私は考えます。
おまけ1 (箱ひげ図を基にしたデッキ作成例)
今回の実験結果である箱ひげ図を基に実際にドラゴンクラスのデッキを作成してみました。
まず、デッキを組むにあたって設定した条件は以下の通りです。
・「絶大の唯我・マゼルベイン」を使うまでに引きたいドロー枚数:9枚
・フィニッシュ札等の可能な限り毎試合使いたいカード (複数枚積みたいカード) の種類数:PP加速札を少なくとも3種類は3積み、フィニッシュ札を3種類以上は複数枚積みたい (ローウェン、ブルータル、ガルミーユ)、「再臨する絶大」もできれば2枚積みたい
・下振れの許容範囲:外れ値は考慮しない
箱ひげ図より、これらの条件に当てはまるデッキ構成は以下の5通りが見つかりました。
「再臨する絶大」複数枚積みを諦めない場合
・3_4_20 ・3_5_18 ・4_3_19
「再臨する絶大」複数枚積みを諦める場合
・3_3_22 ・4_2_21
今回は「再臨する絶大」の複数枚積みを諦めなくていいデッキ構成が3つ見つかったので、その中から 3_4_20 構成を選択しました。
3_4_20 構成についての箱ひげ図と実際に組んだデッキを以下に示します。


複数枚採用したカードは以下の通りです。
「絶大の唯我・マゼルベイン」3枚
3枚採用
「竜の託宣」「独尊龍・スーロン」「イグニスドラゴン」
2枚採用
「再臨する絶大」「竜槍の戦士・ローウェン」「ブルータルドラゴニュート」「烈絶の侮蔑・ガルミーユ」
箱ひげ図を見る限り、隣の 3_3_22 構成が10から20枚までを範囲としてデータが広く分布しているのに対し、3_4_20 構成は11から19枚までの範囲内にデータが集中して分布しています。3_4_20 構成の方では10が外れ値として表示されているのも、このデータ分布の集中度の違いが原因ではないかと考えます。
また、箱ひげ図より「絶大の唯我・マゼルベイン」を出すまでに10 ~ 11枚程度のドローならほとんどの試合で許容されることも見て取れます。
そこで、「導く鐘・ベルエンジェル」や「降臨する干絶」「天使の恩寵」といった、序盤でも使えるドローソースを積んでみました。これにより、マゼルベインやフィニッシュ札などを更に安定して引き込めるようになることが期待できます。
おまけ2 (箱ひげ図 一覧)
実験結果の箱ひげ図の一覧を1枚の画像にまとめたものを以下に示します。

