
二分探索を覚えて欲しい!
ゲームを作る他に専門学校のシステム系学科で外部講師もやってます。
今回は「二分探索」について、詳しくお話したいと思います。
同じ探索アルゴリズムの「線形探索」に比べると複雑。
学生に教えても敬遠されがち(な気がする)「二分探索」がなぜ教科書や問題集に出てくるのか……というお話もしています。
情報関連の勉強をしていて「学校で習ったけどよくわからん」という方や、これからプログラムを勉強しようという方にオススメの内容です。
前回の記事はこちらです!
ちなみにプログラミング学習の関連記事は以下にまとめてます!
二分探索とは?
前回の記事で解説した「線形探索」は探索アルゴリズムのひとつです。
今回の「二分探索」も探索アルゴリズムのひとつで、バイナリサーチともいいます。
念のためWikipediaさんのリンクも貼っておきます→コチラ
つまり、たくさんあるデータの中から必要なモノを探し出すための処理の考え方のひとつですね。「線形探索」と同様に「二分探索」も「基本情報技術者試験」によく出てくるそうです。
余談ですが、わたしが学生だった頃は第二種情報処理技術者試験という名前だったので、どうしても「二種」って略称が頭に浮かんできて…
「違う、違う、基本情報技術者試験!!」って書き直しています。
線形探索と何が違うの?
探索対象のデータ、もしくはデータのキーとなる値が昇順(または降順)に並んでいる場合、線形探索に比べて早く必要データを見つけ出すことができます。
この「並んでいる」というのが重要です。
並んでいない場合(ソートされていない場合)二分探索は使えません。
例題
早速ですが例を挙げて説明しましょう。次の表は美容院の顧客名簿です。
顧客番号74番は誰でしょう?

前回の記事と同様に、プログラムに処理をさせる手順を想像してみます。
線形探索ではデータの先頭(または末尾)から必要なデータか確認していきますよね。この例では顧客番号74番が必要なデータとなります。
配列の先頭に入っている顧客番号は19番、74番ではありません。
配列の次に入っている顧客番号は27番、74番ではありません。
配列の次に入っている顧客番号は35番、74番ではありません(繰り返し…)
配列の次に入っている顧客番号は74番、見つけました! 木下さんです!
これだと必要なデータが配列の後ろの方にある場合、なかなか見つかりません。処理を繰り返し、7回目のチェックで見つけることができました。
では、二分探索の考え方で手順を想像してみます。
配列の探索下限は添字で言うと0、上限は9、中央は4!(小数点以下切り捨て)
配列の4番目は顧客番号51番、74番は51番の後方にあるハズ!
さっきの中央より後方にあるから…
探索下限は添字で言うと4(+1)、上限は9、中央は7!
配列の7番目は顧客番号86番、74番は86番の前方にあるハズ!
さっきの中央より前方にあるから…
探索下限は添字で言うと5、上限は7(-1)、中央は5!(小数点以下切り捨て)
配列の5番目は顧客番号62番、74番は62番の後方にあるハズ!
さっきの中央より後方になるから…
探索下限は添字で言うと5(+1)、上限は6、中央は6!
配列の6番目は顧客番号74番、見つけた! 木下さん!
なんと、線形探索だと7回のチェックで見つけたのに!
二分探索だとたった4回のチェックで見つけました!!!!!
はい、これが二分探索です。いやぁー、いい説明だった!!!!!
「待て待て待てっ! 意味わからん! 面倒臭すぎる!」
というツッコミを入れたくなりますね……
文章で表現すると難しそうなことをしていますもんねぇ。
なので、文章ではなくイメージ図で想像してみましょう。
二分探索の仕組みを図で説明
問題を単純化するために、顧客番号の部分だけで説明しますね。

探索範囲の下限が0、上限が9なので、その中央は (0+9)÷2 で求められます。
小数点以下切り捨てで中央は4、顧客番号の配列kNo[4]は51番でした。
二分探索はデータもしくはデータのキーとなる値が昇順(または降順)に並んでいる場合に使用可能です。顧客番号は昇順に並んでいますね。なので、kNo[4]に入っていた51番より、探している74番は配列の後ろにあると判断できます。

kNo[7]は86番です。
探していたのは74番、つまり現在の中央より前にあるハズです。
ご覧の通り、探索範囲がぐっと狭くなりましたね!

探索範囲が狭まってきました。
もう少しで探しているデータを確定できますね!

フローチャート
顧客番号74番は誰なのか名前を表示するフローチャートを書いてみました。
(※ 線形探索に比べると複雑で細かいです。拡大してご覧ください!)
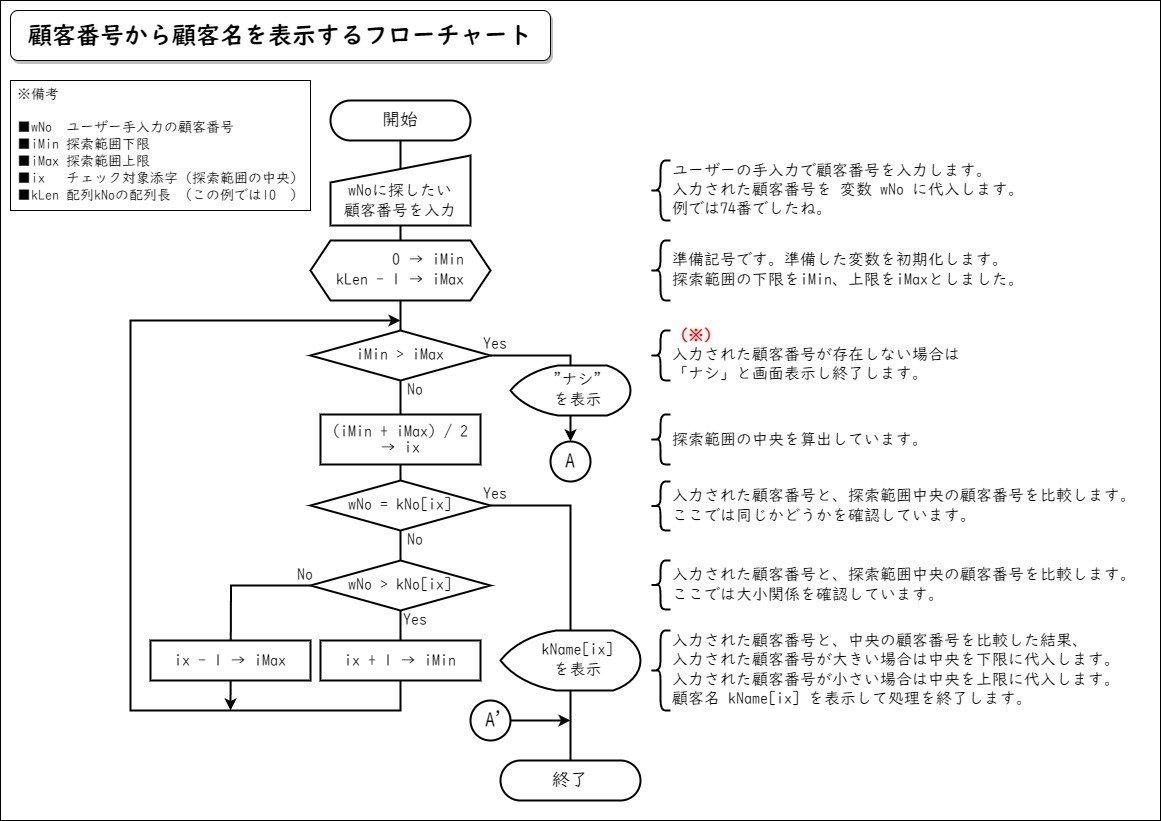
二分探索のフローチャートは、大体がこんな形になると思います。
「理屈で考えると難しそう」と思う方は、こんな形になると記憶しちゃった方が楽かもしれません。
さて、このフローチャートには、ここまで説明した「二分探索の処理の流れ」に更にひと手間を加えています。赤文字の(※)の部分に注目!
「探索範囲の下限と上限を比較して、下限が上限より大きくなってしまった場合は"ナシ"と画面表示して終了する」という流れになっています。
これは入力された顧客番号が配列kNoに存在しない時に発生します。
システム的にあり得ない顧客番号は入力されない仕組みがあるなら、この部分は不要ですが、エラー対応されていると丁寧に感じますよね。
プログラムコード(VBA)
フローチャートを参考にプログラムコードを書いてみます。
今回もVBAで処理してみますよ。

Excelで上図のようなデータとユーザーフォームを作りました。
「顧客番号」のところに手入力で番号入力をして、「番号検索」ボタンを押すと名前が表示されるようになっています。
プログラムコードはこんな感じになりました。
Option Explicit
Dim kNo(9) As Integer '【配列定義】顧客番号のデータが入る配列
Dim kName(9) As String '【配列定義】顧客名 のデータが入る配列
Dim kAge(9) As Integer '【配列定義】年齢 のデータが入る配列
'──────────────────────────────────────────────────
'
' ユーザーフォームがアクティブになった時に発生する
'
'──────────────────────────────────────────────────
Private Sub UserForm_Activate()
Dim ix As Integer '【変数定義】配列にデータを入れるための添字
For ix = 0 To 9 '■ 初期データを代入しておくループ
kNo(ix) = Sheet1.Cells(2, ix + 3).Value '├ Sheet1の顧客番号を配列kNo に代入
kName(ix) = Sheet1.Cells(3, ix + 3).Value '├ Sheet1の顧客名 を配列kNameに代入
kAge(ix) = Sheet1.Cells(4, ix + 3).Value '└ Sheet1の年齢 を配列kAge に代入
Next ix
TextBox1.Text = kNo(0) 'ユーザーフォームのテキストボックス1に配列kNo(0)を入れておく
End Sub
'──────────────────────────────────────────────────
'
' 【二分探索】
' 顧客検索のボタンを押された時に発生する
'
'──────────────────────────────────────────────────
Private Sub CommandButton1_Click()
Dim wNo As String '【変数定義】入力された顧客番号
Dim iMin As Integer '【変数定義】探索範囲の下限
Dim iMax As Integer '【変数定義】探索範囲の上限
Dim ix As Integer '【変数定義】チェック対象添字(探索範囲の中央)
Dim kLen As Integer '【変数定義】配列kNoの配列長
wNo = TextBox1.Text '[初期設定]テキストボックス1に入力された顧客番号をwNoに代入する
kLen = 10 '[初期設定]配列長 10件
iMin = 0 '[初期設定]探索範囲の下限 0
iMax = kLen - 1 '[初期設定]探索範囲の上限 9
TextBox2.Text = "ナシ" '[初期設定]顧客名の表示テキストボックスに「ナシ」を入れておく
Do While iMin <= iMax '■ 探索範囲の下限が上限より小さいか同じ場合はループし続ける
'│
ix = (iMin + iMax) / 2 '├ 探索範囲の中央を算出する
'│
If wNo = kNo(ix) Then '├◆「入力された顧客番号」と「顧客番号配列の探索範囲中央」が同じ場合
TextBox2.Text = kName(ix) '│├ 顧客名の表示テキストボックスに顧客名を代入しておく
Exit Do '│└ このループを抜ける
End If '│
'│
If wNo > kNo(ix) Then '└◆「入力された顧客番号」が「顧客番号配列の探索範囲中央」より大きい場合
iMin = ix + 1 ' ├ 中央値 + 1 を探索範囲の下限に代入する
Else ' ◆ そうではない場合
iMax = ix - 1 ' └ 中央値 - 1 を探索範囲の上限に代入する
End If
Loop
End Sub今回のフローチャートで表現したプログラムコード(二分探索)は
「Private Sub CommandButton1_Click()」 から 「End Sub」 までです。
それ以外の部分はExcelシートからデータを取得している部分ですね。
もっと短く書くこともできますが、今回は二分探索のフローチャートから逸脱しないようにコード化しています。
コード内で何をやっているかは、コードの行末にコメント化し置いているのでそちらをご覧ください。人のコードを見ると参考になると思いますよ。
やっぱり難しい二分探索!
やってることは理解できたような、できないような。でもさぁ~
「やっぱり線形探索に比べると面倒くさいよ!」
その気持ちわかります。難しい、ホント難しいんですけど…
例は10件程度のデータなので、ありがた味を感じないんですよね。
じゃぁ、ありがた味を感じましょう!
そしたら覚えますよ、きっと!
1から1ずつカウントアップして10000までのデータがあるとしますよ。
つまり、1万件のデータが並んでいます。そして9420を探すとします。
線形探索で先頭からチェックすると9420回目のチェックで発見です。
線形探索で末尾からチェックすると580回目のチェックで発見です。
二分探索だと…
ここで単にチェック回数を計算式でお見せしても、ありがた味が薄れるので実際にやってみますよ。
【1回目の処理】
範囲下限が1、上限が10000、中央が5000、9420は中央より後方にあることがわかります。下限を5001にしましょう。
【2回目の処理】
範囲下限が5001、上限が10000、中央が7500、9420は中央より後方にあることがわかります。下限を7501にしましょう。
というのを繰り返したメモが以下の表です。

たった12回のチェックでみつけました!
こうやって考えると、効率よさそうですよね~!
ほら、覚えた方が良さそうですよ!
資格試験、教科書、問題集に出てくる理由もわかりますね!
実装上の間違い?
この記事の最初の方に貼ったWikipediaさんの「二分探索」なんですけど、この中に「実装上の間違い」という項目があります(2024/07/20に確認)
ドナルド・クヌースは "Although the basic idea of binary search is comparatively straightforward, the details can be surprisingly tricky ..."(二分探索の基本的なアイディアは比較的平易だが、その詳細は驚くほど扱いが難しいものになりうる)と述べており[2]、二分探索が正確に実装されていないことは多い。Richard E. Pattis の1988年の調査では、書籍20冊のうち15冊が誤っていた[3]。
よくある間違いの一つは、上記のC言語のコードで imin + (imax - imin) / 2 を (imax + imin) / 2 としてしまう事である。(imax + imin) / 2 では、imax + imin が int の値の上限 (INT_MAX) を超えて不正な値になってしまう可能性がある。(imax + imin が INT_MAX を超える可能性が全くないと保証できる場合は問題ない。)
「なんじゃこれ?」と、思うかもしれません。
C言語の変数型である「int」は4バイトの整数数値を入れる変数型です。
扱える範囲は -2,147,483,648 ~ 2,147,483,647 です。
「もし、すごく大量のデータの二分探索をするときにint型を使っているとint型の上限を超えちゃう。そうすると計算できないよ!」という意味です。
あら、たしかに不具合発生しそうですね。
「どういうこと?」
先程のVBAのプログラムコードではInteger型の変数で処理してます。
VBAのInteger型が扱える範囲は -32,768 ~ 32,767 なので上限超えるかも?
「だから、どういうこと?」
説明すると
(例)3万件のデータがあり、目的のデータは27810件目とします。
【1回目の処理】
範囲下限が1、上限が30000、中央が15000、27810は中央より後方にあることがわかります。下限を15001にしましょう。
【2回目の処理】
範囲下限が15001、上限が30000、中央が…
中央の計算を(下限+上限)して、÷2をするという計算式だと
VBAのInteger型が扱える範囲、32767を超えてるから危ない!
試してみましょう。
Dim ix As Integer
Dim iMin As Integer
Dim iMax As Integer
iMin = 15001
iMax = 30000
ix = (iMin + iMax) / 2
MsgBox ix

やっぱりオーバーフロー(つまりInteger型の最大値を超えた)しました。
では、どういうプログラムコードを書けばいいのか?
この部分を…
ix = (iMin + iMax) / 2このように…
ix = iMin + (iMax - iMin) / 2書けば大丈夫。という話をしているんでしょうけど、まぁ、個人規模のゲームならそこまでのデータ量はないので大きな問題にはなりません…けどね、

わたしが持ってる問題集には記載が無かったので、一応説明でした!
頭の片隅に置いて大量のデータを扱う時に思い出してください…
おわりに
「二分探索」理解できたでしょうか?
ちょっと難しいけど、効率は良さそうですよね。
もちろん、システム系学科の学生だったら教わると思いますし、
最低限、わたしが担当する授業内容には含まれています。
(…ということは、ある意味で有料級の記事かもしれない!!)
冗談はさておき、
基本情報技術者試験の問題集にも二分探索について書かれているので覚えた方が良いです。なぜ学習するかはこの記事中にありましたよね?
今後もアルゴリズムやフローチャートといったプログラミング学習関連については記事にしていきますので、勉強したい方は一緒にがんばりましょう!
解説だけじゃなく、練習問題と解答例をまとめた記事にしてもいいかも…と考えてたりします。
すごく難しそうなことを書いていますが、普段はこんなゲームを作っているサークルの人です。ご興味がございましたらご覧ください(↓)
それでは、また別の記事でお会いできるのを楽しみにしております!
いいなと思ったら応援しよう!

