【偏差値経由法】複数の種目の別種目への換算
本記事では、あるスポーツの種目を別のスポーツの種目と比較するため、これを換算する方法を述べます。これは公式なものではありません(そもそも公式な換算方法は存在しないと思われます)。
換算用データ
換算をするためのデータとして、水泳と、サイクリングのデータを用意しました。記録は「大きい数値を良い記録」として扱うことができるように、すでに速度(ミリメートル毎秒)に換算されているため、距離がいくらかであるかは問題になりません。


本記事で説明する方法は、「偏差値経由法」と命名しました。
標準偏差と偏差値
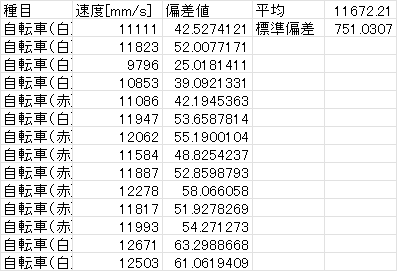
このデータから標準偏差と偏差値は、次のように算出されます(STDEV.Sを使用)。

近似曲線の式を作成
元のデータとその偏差値から散布図を作成し、その近似曲線を求めると、相関係数は1となり、下図の一次関数が得られます。


水泳から自転車に変換
サイクリング(以後「自転車」と表記)のデータ→偏差値の関数はy=0.0133x-105.42であるため、この逆関数を求めます。
-0.0133x=-105.42-y
x=(-105.42-y)/(-0.0133)←これが逆関数
上記の逆関数のyに、水泳のデータ→偏差値の関数を代入します(ここでは、水泳のデータをx'とおく)。
x=(-105.42-(0.1695x’-71.93))/(-0.0133)
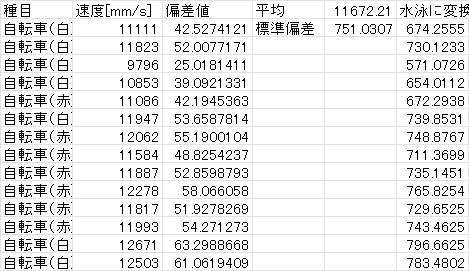
ゆえに、水泳の記録を自転車の記録に換算する(単位はいずれもmm/s)と、下表のようになります。

自転車から水泳に変換
水泳のデータ→偏差値の関数はy=0.1695x-71.93であるため、この逆関数を求めます。
-0.1695x=-71.93-y
x=(-71.93-y)/(-0.1695)←これが逆関数
上記の逆関数のyに、自転車のデータ→偏差値の関数を代入します(ここでは、自転車のデータをx'とおく)。
x=(-71.93-(0.0133x'-105.42))/(-0.1695)
ゆえに、自転車の記録を水泳の記録に換算する(単位はいずれもmm/s)と、下表のようになります。