
Tableau数学 - 1. Spiral Histogram
ようやく#Makeovermondayデビューをしたおつうです。
運営のAndy KreibelからもReplyを頂き上機嫌な私ですが、今回はその仕組みについて数学の考え方から解説したいと思います。
Viz for #MoM2023 | Week23
— おつう (@tsu_chaan) June 10, 2023
Pedestrians in Melbourne from SEASONAL perspective.https://t.co/tNg1IlnPSO
This is my first #makeovermonday :)
enjoyed. thanks : @VizWizBI pic.twitter.com/AywvhhfFyO
アイディアの根源
独創性の高いVizを作りたいと思ったときに、私が参考にしているのがコチラ。いろいろなチャートからイメージを膨らまし、「面白そう」という安直な理由から、今回のテーマであるSpiral Histogramにたどり着きました。
データの準備
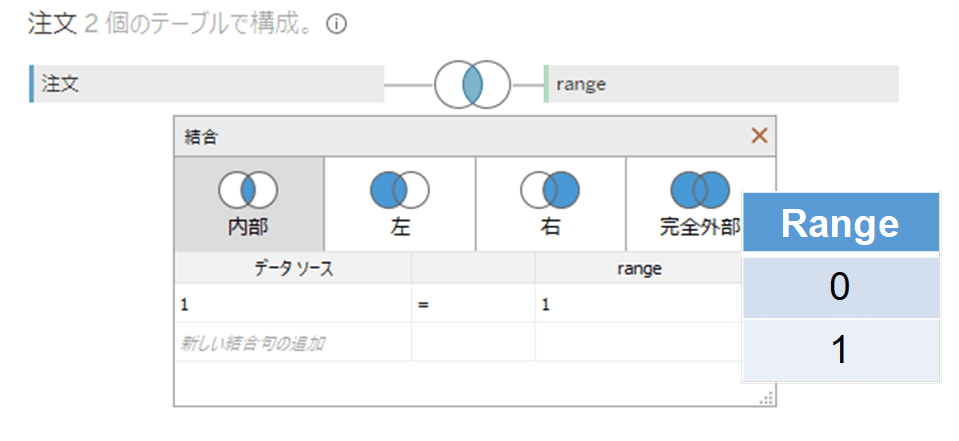
今回のデータ準備における大事なポイントは「行の複製」です。Spiral Histogramでは、螺旋の内側と外側の2点の座標を指定する必要があります。どちらも同じデータですが、別の座標として区別したいので、Rangeというデータテーブルを使って2行に複製しています。
三角関数の基礎
Spiral Histogram や Radial Chart などで避けて通れないのが、三角関数(sin, cos)です。この時点で、拒絶反応が出る人も多いかと思いますが、最低限の数学の知識は、しっかりと説明することをモットーにしてますので、是非お付き合いください。
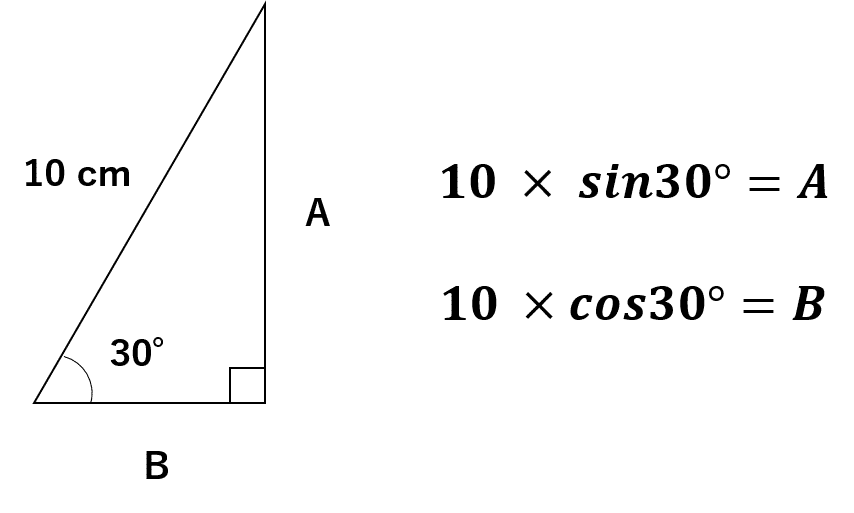
といっても、今回使うのはこれだけです。直角三角形の「角度」と「斜めの長さ(斜辺)」が分かっていたら、残りの2辺の長さも分かる、というのが三角関数です。「sin30°はいくつなの?」という疑問が生まれますが、安心して下さい。はいてま……Tableau関数が計算してくれます。
円の座標で考える
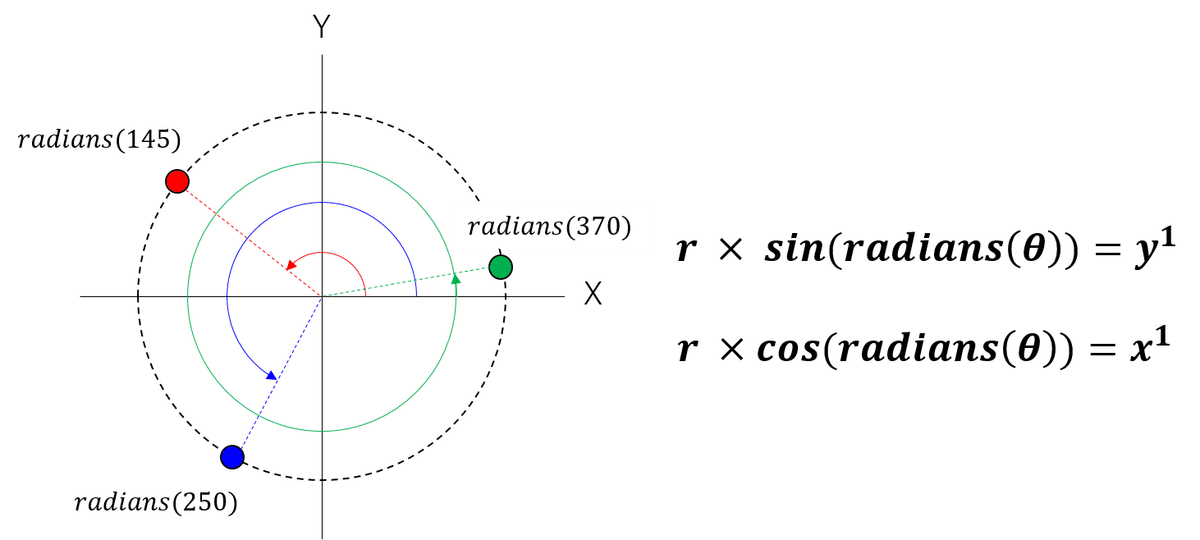
さて、今回の主役である「円」について考えてみます。円の中心の座標を(X, Y) = (0, 0) としたときの図が以下です。
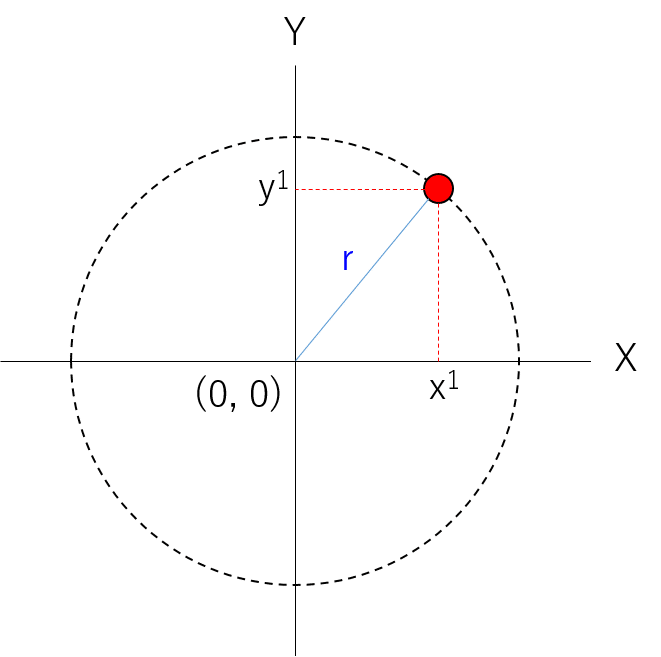
お気づきかと思いますが、直角三角形が見えませんか?
・斜辺の長さ = 円の半径
・角度 = X軸からの角度
つまり、円周上にある点の座標 (x1, y1) は、以下のようにあらわすことが出来ます。これが円の方程式です。
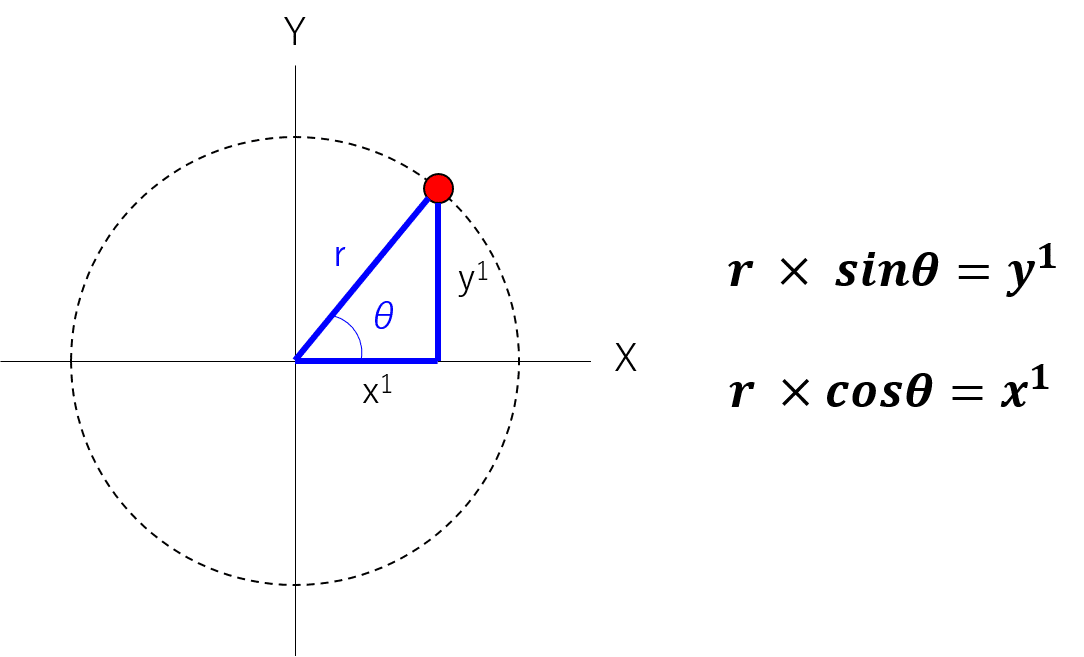
角度が90°を超えて、直角三角形が裏返しになったところはどうするのか?という疑問に対してはRADIANS関数が有効です。X軸からの角度を変換してくれます。360°を超えて一周回ったとしても、問題ありません。
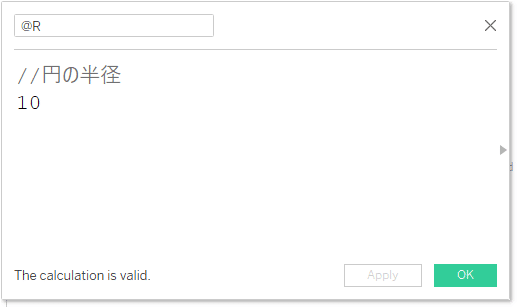
円を描いてみる
まずはじめに、円の半径となる計算フィールドを作ります。ひとまず半径は10とします。
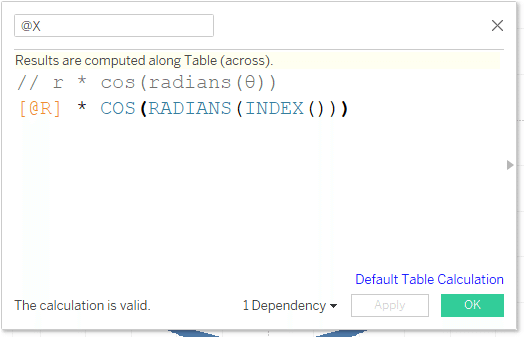
次に先ほどの三角関数を使って、X,Y座標を作ります。角度に相当する部分は、データに行番号があればそれでも良いのですが、今回はindex関数を使っています。
ここまでくれば、円が描けます。行シェリフに計算式の@X、列シェリフに@Yを入れます。indexの基準となるディメンション(オーダーID)を「詳細」に入れて、それぞれの表計算の「次を使用して計算」で指定します。
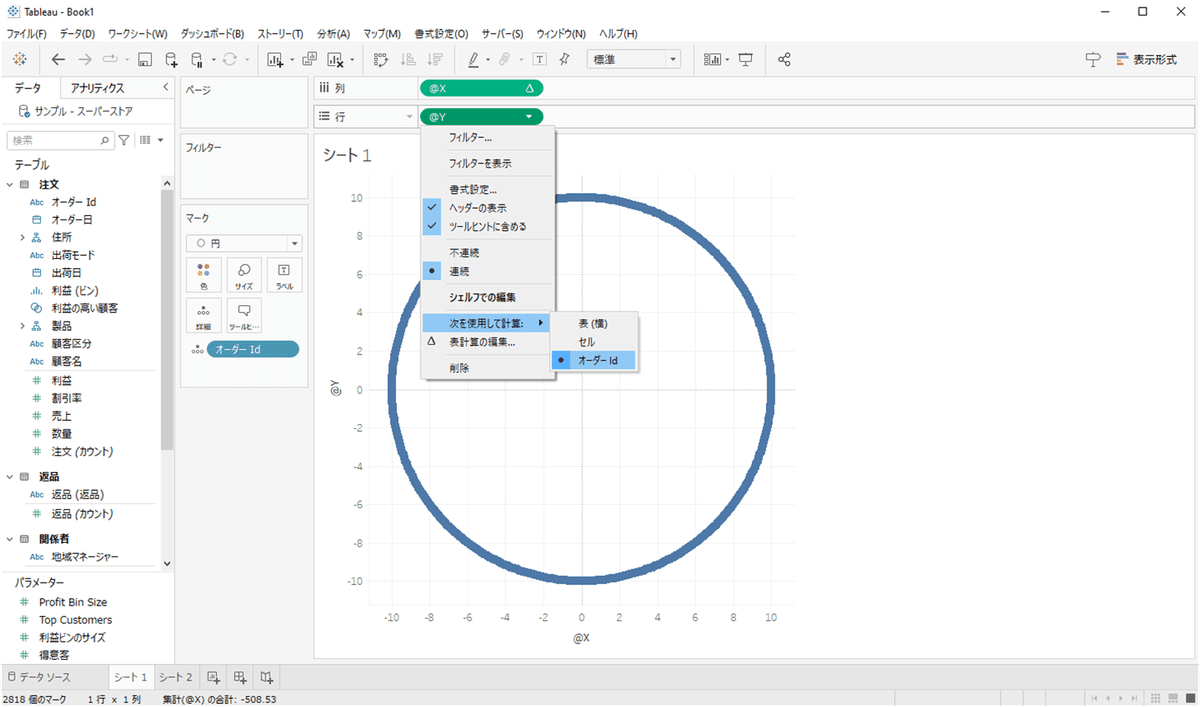
この時、とても重要なことは、「何周もの円が重なっている」ということです。マークの数を見ると、オーダーIDが2818個あることが分かります。円の一周は360°なので、2818マーク(=index) ÷ 360° ≒ 7.8 周。私は、Raidal Chartを作る上でこの感覚がとても重要だと思っています。
もしピッタリ1周分の円を描きたいならどうすればよいでしょうか?360°をマークの数で割ります。するとindexが最大値(=マークの数)になった時に、ちょうど360°になります。マークの数はSIZE関数を使うと簡単に求めることができます。
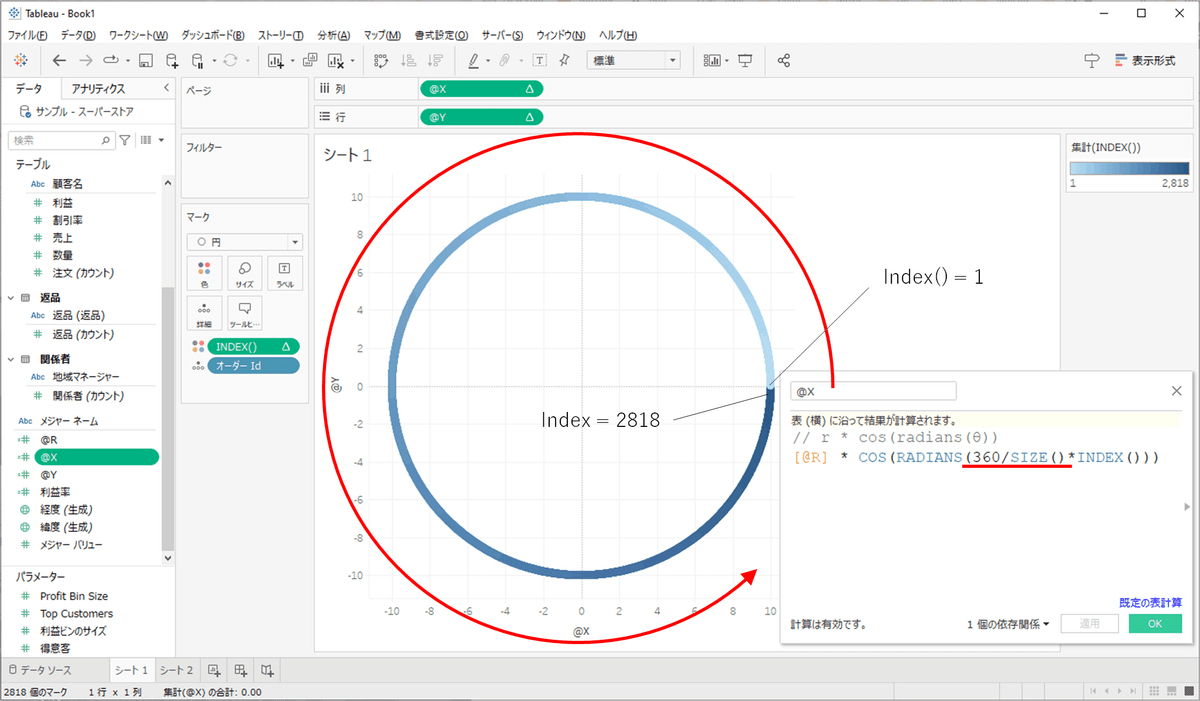
わかりやすいようにindexを色にしました。0°のところから始まり、indexが最大値になったところで一周しています。360° / sizeは、indexがひとつ増えた時に、どれだけ角度を進めるか?を計算していることになります。今回は螺旋にしたいので、3周円を描きます。360° × 3 = 1080° ですので、1080 / size( ) * index( ) とすればよいことが分かっていただけたでしょうか。
螺旋にする
ここからは3周分の円を螺旋にする方法を考えてみます。螺旋にするには、徐々に円を大きくすればよいです。例えば、スタート地点(0°)では10だった半径が、半周(180°)で11に、一周(360°)したら12になります。
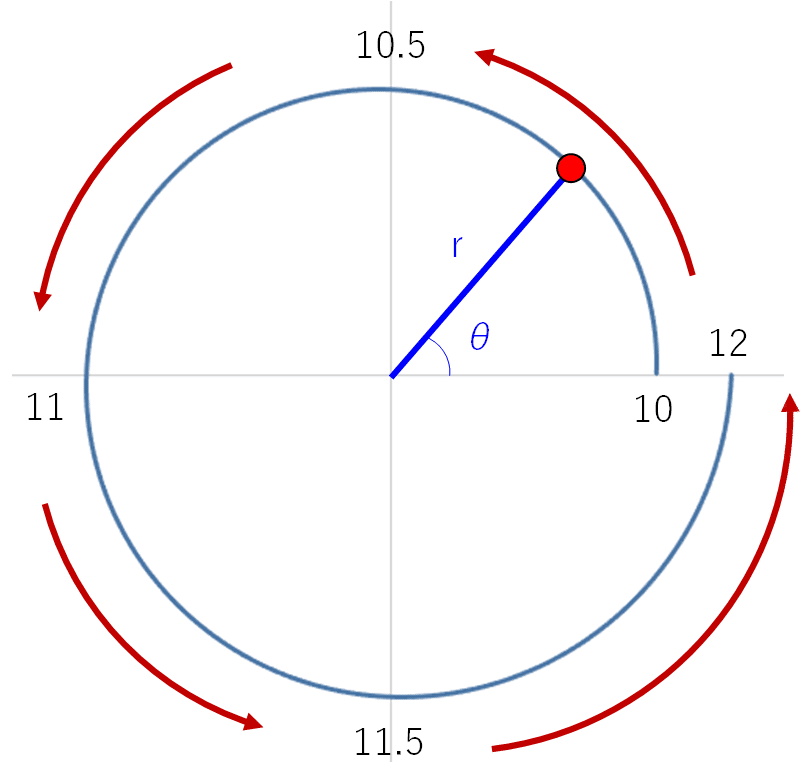
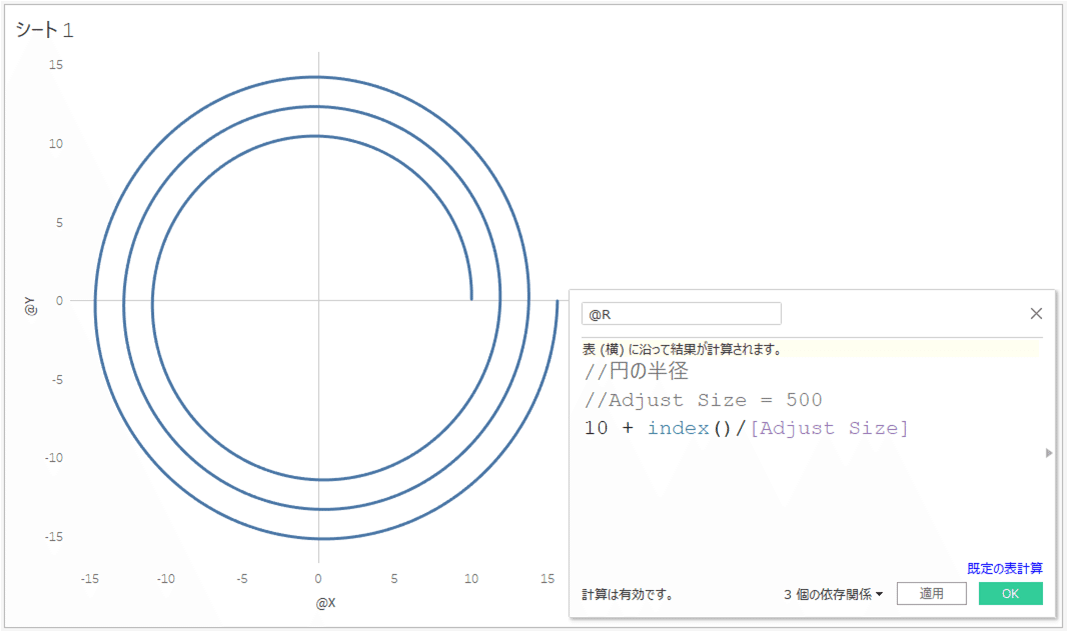
つまり、最初に作った半径にもindex関数をかけることで、少しずつ半径が大きくなります。この時、広がり具合を調整するために、パラメータを使ってもいいかもしれません。
棒グラフにする
さて、最後に螺旋状の棒グラフにしてみます。漸くここで、最初に行を複製するために用意したRangeというフィールドを使います。この時、Range = 0 は棒グラフの始点、Range = 1 は棒グラフの終点として考えてみます。
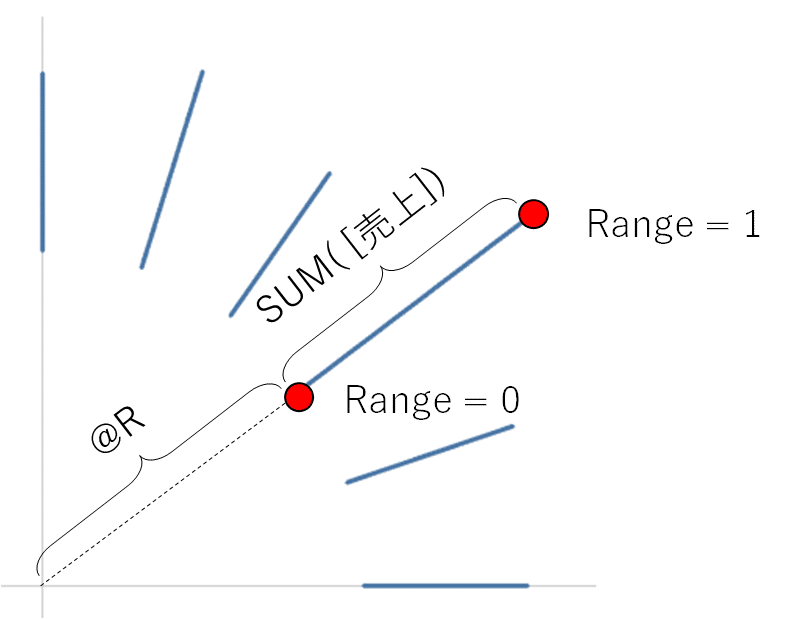
始点は今まで作った計算式のまま、終点だけ何かのメジャーを半径に足してあげればよいです。ここで使うのがIF関数です。
やや式が複雑になってきましたが、追加したのは IF関数による分岐 と 終点の半径にSUM ( [売上] ) を足しただけです。MAX ( [Range] ) = 0 としている理由は、集計/非集計のエラーを回避するため。メジャーをそのまま入れると棒グラフが突き抜けてしまいますので、パラメーターで調整して下さい。
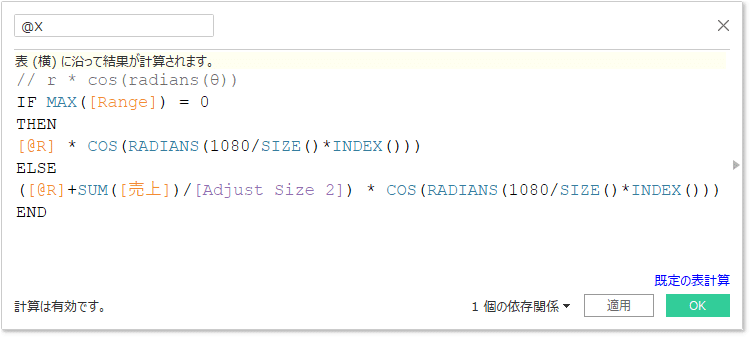
最後の仕上げは、パスを設定することです。グラフの種類を線にしても、以下の図のようにすべての線が繋がってしまい、うまくSpiral Histogramを描くことができません。
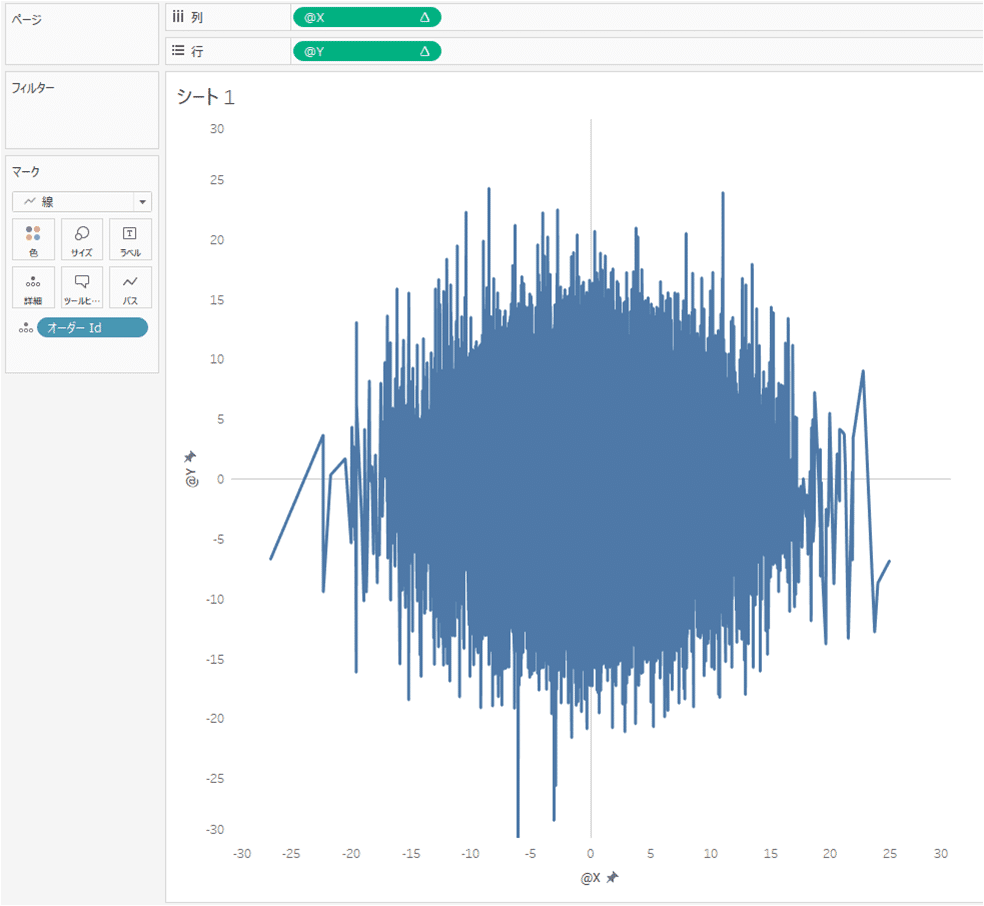
そこで、Rangeをパスに落とします。この時、メジャーではなくディメンションに変更することを忘れずに。こうすることで、線の始点と終点はRangeを基準に繋がれます。
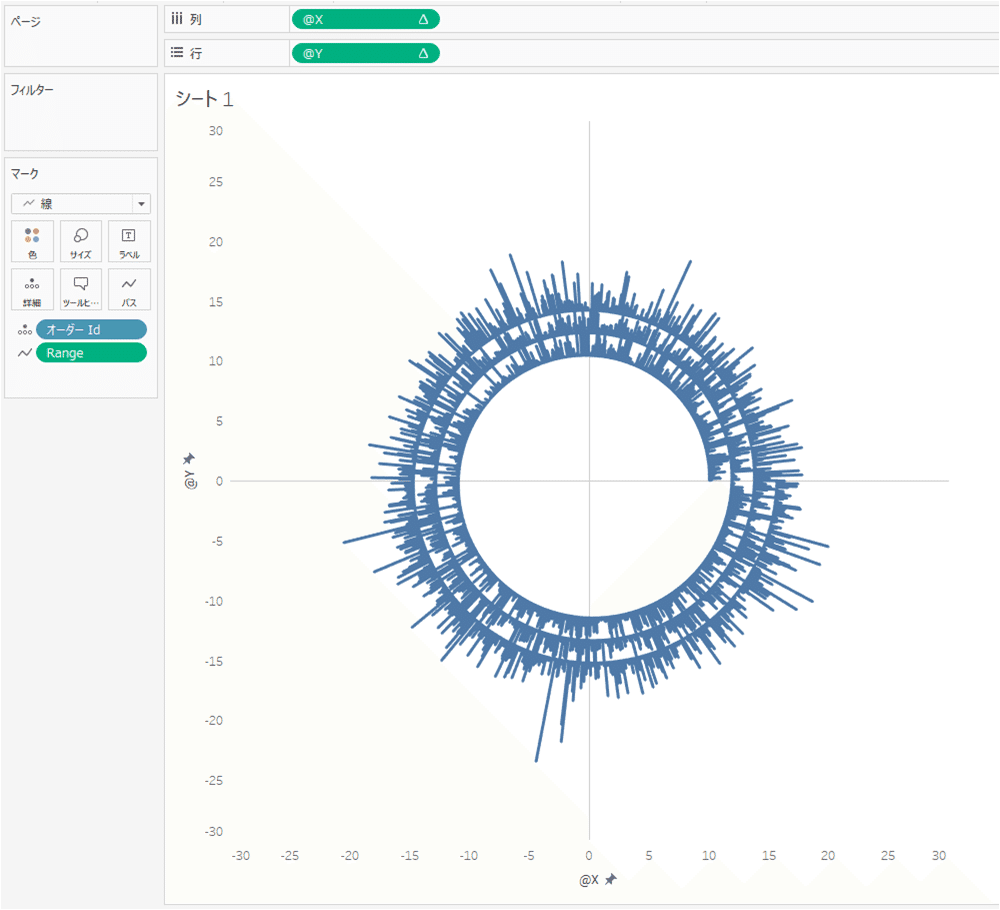
ここまでくれば、Spiral Histogramの仕組みが数学的に理解できたのではないでしょうか?随所に出てきた数字やパラメーターを調整することで、好みの形にすることができると思います。色などを追加する場合は、表計算に影響がないように、属性で入れて下さい。
まとめ
用意された計算フィールドをコピー&ペーストし、メジャーを入れ替えるという作業の方が、独創的なVizを作ることは容易ですが、私は計算式の中身を理解することをいつも心がけています。仕組みを理解できれば、自分なりにカスタマイズが出来て、更なる新しい発見に繋がります。今回の記事を読んで、少しでも数学に対する敷居が下がり、Radial chartに対する見方が変わってくれれば、と思っています。
それでは、また。
