
Tableau数学 - 3. Rose Curve : バラ曲線
はじめに
先日のTableau Viz 紅葉 キャンペーンでは、たくさんの「like」ありがとうございました。サンプルスーパーストアだけで作っところが良かったのか、さかぴーさんの「Tableau曲線表現講座」のおかげか、1位を頂けました。ずっと「こうよう」ではなく「もみじ」だと思ってましたが、お許しください。
#Tableau曲線講座 からラジアルチャートがHotなので、サンプルスーパーストアから #紅葉 を作りました。これを Maple Curve 🍁と名付けます。
— おつう (@tsu_chaan) November 22, 2024
楽しい企画をありがとうございました。#TableauViz #PRhttps://t.co/hoZM6dmP4c pic.twitter.com/3HCZbhSNlD
毎年参加させていただいてる、Tabjo Advent Calendarですが、今年で3回目の挑戦になります。去年は、投影図についてお話しましたが、今年はTableau数学の第3弾として、もみじを描くアイディアにもなったバラ曲線について執筆してみようと思います。
バラ関数とは?
はじめに、バラ関数の美しさを一言で表すならば、式が非常に「シンプル」であることです。

極座標とは、タテヨコではなく、半径と角度で座標を定義する方法で詳しくは Tableau数学 - 1. Spiral Histogram をご覧ください。θが角度で、rが半径です。nとdに任意の数字を入れると、様々な曲線が描けます。とりあえず、このVizを見てください。

たった一行の式ですが、(d, n)の組み合わせ次第で、様々な曲線が描けます。d = 1 のお花も好きですが、何といっても(3, 4)や(5, 4) なんかは圧巻ですね、なんて美しい。では、なぜこのような美しい曲線になるのか?極座標と直交座標を組み合わせてみるとよくわかります。
直交座標系で考える
まずは、一番シンプルな (d, n) = (1, 2) で考えてみます。
角度(θ)はわかりやすいように0°から360°まで変化させます。今回のデータは1~360までの数字を用意しましたが、デンシフィケーション(Data Densification)を使っても良いです。デンシフィケーションについてはArakawaさんのNoteが最もまとまってると思います。
あとは、以下のような計算フィールドを作りました。RADIANS関数を使って角度をラジアン単位に変換することをお忘れなく。

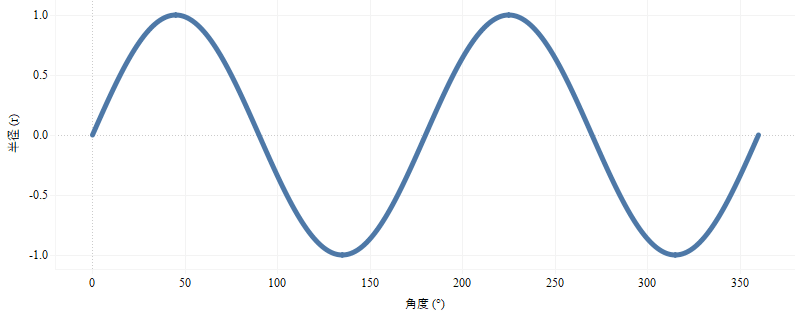
この計算フィールドを直交座標系、つまり、タテが半径(計算結果)、ヨコが角度( [Id] = 0 ~ 360°)で表したものが以下です。ポイントは、山が2つと谷が2つ。山はプラス(0 ~ 1)で、谷はマイナス(-1 ~ 0)です。
「ラジアン」って何?
少し脱線しますが、曲線の話をすると毎回出てくるラジアンについて、少し丁寧に説明します。
「円の1周は何度ですか?」と聞かれたら、360°と簡単に答えられます。ただし、「それは何ラジアンですか?」と聞かれたら、「は?」となってしまうか、360°=2π [rad] と丸暗記しているが、理由を説明するのは難しい、という人が多いはずです。

ラジアンは「弧度法」といい、その名の通り、弧の長さを基準に角度を決めました。半径1の単位円において、弧の長さが1進んだ角度を1ラジアンとした、ただそれだけです。つまり1周(360°)した時の弧の長さはイコール周長となるため、直径 × 円周率 から 2π を求めることができます。なので、1周を360°としても、2πとしても、ものさしが違うだけのことですが、SIN関数やCOS関数の括弧の中は、このラジアン単位で入力することに決まっています。これは、三角関数の微分などより複雑な計算をした際、ラジアン単位のほうが便利だからです。
直交座標系と極座標系を動かしてみる
本題に戻りますが、r = sin (2θ) のバラ曲線を動かしてみます。角度(θ)が増えていくと、直交座標、曲座標ではそれぞれどのような軌跡を描くのか確認してみます。

最初の90°まで半径 (r) は滑らかに「山」を描き、花びらが1枚描かれます。理解を複雑にしているのは、次に現れる「谷」の部分です。半径がマイナスとはどういうことか?これは数直線と同様に、負の向き(角度で180°反対側)に点を取るということです。なので、角度(θ)は赤矢印の向きに進んでいますが、花びらが描かれる順番は①~④と逆向きになります。

では (d, n) = (1, 3) つまり、r = sin (3θ) の時はどのような軌跡になるでしょうか?

r = sin (3θ) のグラフは、山が3つ、谷が3つになりました。そして、0~180°までに書いた花びらを、次の180~360°までにもう一度描いていることが分かります。d=1の範囲では360°あれば最低1周以上するので、綺麗な花びらが描けますが、d>=2の範囲では360°では足りなくなります。

なので、360°以上のデータ行を用意するか、RADIANS関数の中で角度を2倍、3倍にしてください。ただし、後者はやりすぎると曲線が粗くなるので注意。
プラスの領域だけで考えられないか?
ここから紅葉を描こうと考えた時に、半径がマイナスの計算は難しすぎました。なので、もっとシンプルに、半径がプラスだけで考えようと思い、とりあえず先ほどのバラ曲線の全体を+1してみます。


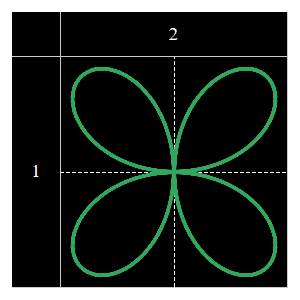
マイナスがなくなったら、反対側に花びらを描いてくれないため、花びらの枚数が4枚から2枚と半分になりました。そこで、山と谷の数を倍にするために、nを4にしたものが以下です。

ここまでくると、バラ関数の仕組みがなんとなく理解できました。山の数で花びらの枚数を調整して、あとは山の形を変えたら、様々な花びらが描けそうです。
角花びらの先を尖らせる
もみじの葉っぱは先端が尖っていますが、今回のバラ曲線はSIN関数を使っているため、山の頂上がどうしても丸くなってしまいます。では、折れ線グラフのようなギザギザした波を作ってみたらどうなるでしょうか。

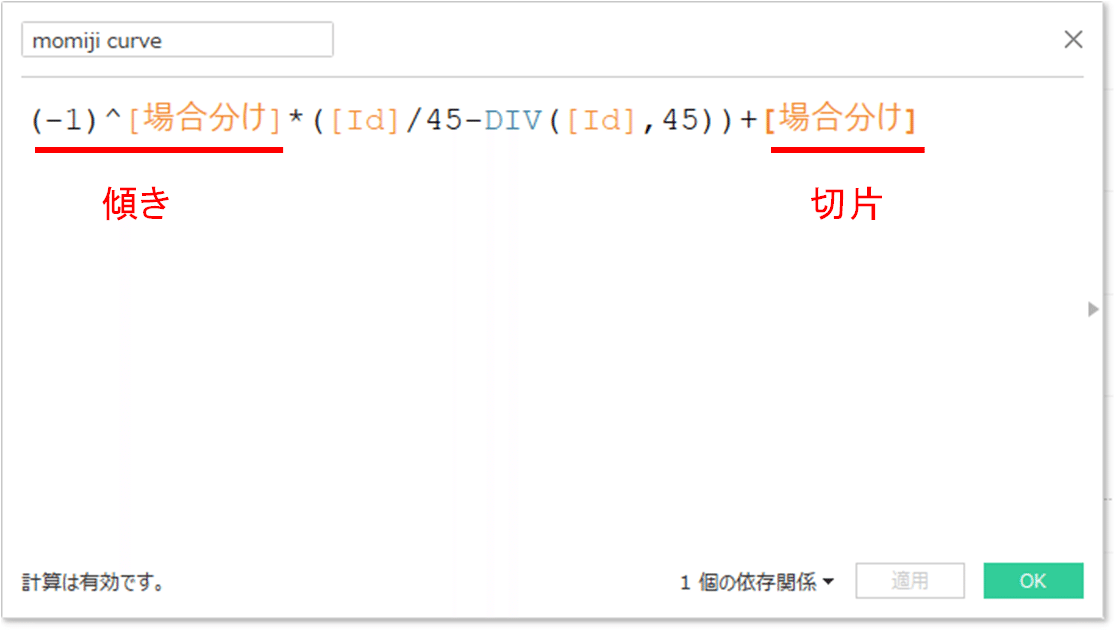
ここから先はどうやってこのギザギザを作るかですが、360°を8等分して、奇数(1,3,5,7)は右上がり、偶数(2,4,6,8)は右下がりと2つの計算式に分けて考えました。


DIV関数は第1引数を第2引数で割った時の商を返します。7 ÷ 2 = 3 あまり1なので、DIV(7,2) = 3 となります。一方で「%」はMod関数(Tableaにはない)と同じで、あまりを返します。ですので、% 2 が「0」なら「偶数」、「1」なら「奇数」という判定式を作れるわけです。

ここまできてようやく、もみじに近い花びらの形になりました。あとは、花びらの枚数を5枚にして、下側にはふくらみを持たせて、などと試行錯誤を繰り返しながら、計算フィールドを作っていくしかありませんでした。
最終的には2つの線を組み合わせた
1つの関数だけでは表現に限界があったため、2つの関数を組み合わせました。F1では、ギザギザ関数を応用して葉っぱの形状を表現。場合分けも駆使して、葉っぱの下側が滑らかになるようにしました。F2ではSIN関数を使って葉っぱの上側の曲線的な膨らみを表現しました。細かいパラメータを調整して、ようやく完成したのが以下のもみじ曲線です。


細かい部分は、PublicのVizをダウンロードして解体していただければと思います。
おわりに
今回は、バラ曲線の美しさをどうしてもお伝えしたくて、かなりマニアックな内容になってしまいました。中身がよくわからなくても、偶然の産物から、突然素敵なVizが生まれたりすることが多々あります。みなさんも是非一度、Tableauで計算フィールドを作って遊んでみてください。
