環論入門part1.1　環の例

※この記事は環論入門part1の補足的な内容です。
※間違いがあれば教えてください

1.3.整数環

命題１
整数全体からなる集合をℤとすると、これは足し算+と掛け算×に関して環をなす。

（証明はほぼ明らかなため省略する）

Rem
命題１のℤを有理整数環とよぶ。

命題２
集合ℤ[√－1]:={a+bi|a,b∈ℤ}⊂ℂは足し算+と掛け算×に関して環をなす。

（こちらも証明は省略する）

Rem
命題２のℤ[√－1]をガウス整数環と呼ぶ。

1.4.多項式環

定義１
・非負整数nと可換環Rに対し、a₀+a₁x¹+...+aₙxⁿ（a₀,a₁,...,aₙ∈R）を文字xに関するR上の多項式という。またこのとき、xを不定元または変数と呼ぶ。さらにa₀+a₁x¹+...+aₙxⁿに対しaₘ（0≦m≦n）をm次の係数という。
・文字xに関する可換環R上の多項式全体からなる集合をR上の多項式環といい、R[x]と表す。

Rem
文字xに関する可換環Rの多項式a₀+a₁x¹+...+aₙxⁿを以下のように表すこともある；

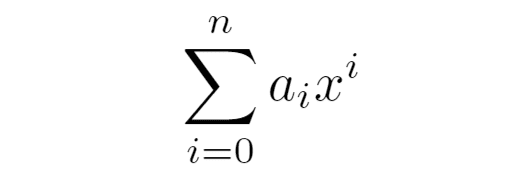
以下では多項式環が環であることを証明していく。

定義２
非負整数m,nに対し、文字xに関する可換環R上の多項式F(x),G(x)を次のように定める。

このとき、R[x]上の加法+と乗法×を次のように定める；

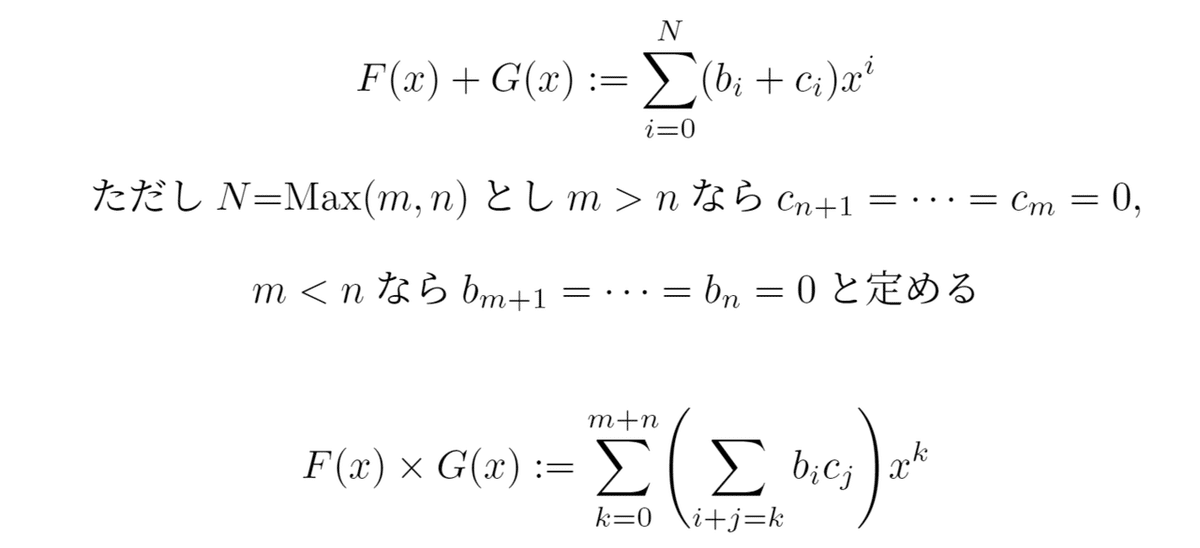
Rem
Rの各元はR[x]の元でもある。実際、Rの任意の元rはr+0x+...+0xⁿと考えることができるため、r∈R[x]が成り立つ。

命題３
R[x]は加法+に関してアーベル群となる。

証明
・結合法則は以下の通り。ただし、以下の計算でm,n,lは非負整数であり、便宜的にm≧n≧lとするがRの+に関する可換性からこれは一般性を失わない。

・Rの単位元0はR[x]の単位元でもある。実際、0=0+0x+...+0xⁿとかけるため、任意のF(x)∈R[x]F(x)+(0+0x+...+0xⁿ)=(0+0x+...+0xⁿ)+F(x)=F(x)が成り立つ。
・F(x)=a₀+a₁x¹+...+aₙxⁿに対し、－F(x):=(－a₀)+(－a₁)x¹+...+(－aₙ)xⁿとすればF(x)+(－F(x))=(a₀－a₀)+(a₁－a₁)x¹+...+(aₙ－aₙ)xⁿ=0となるため－F(x)がF(x)の逆元となる。
・交換法則は以下の通り

▢

命題４
Rが可換環ならばR[x]は可換環である。

証明
命題３からR[x]は+に関してアーベル群であるから、乗法×に関する条件を示す。
・結合法則は以下の通り。ただし、証明の中ではRの分配法則をもちいた。

・Rの×に関する単位元1はR[x]の単位元となる。実際、1は1+0x+...+0xⁿとかけて、任意のF(x)∈R[x]に対して1×F(x)=F(x)×1=F(x)が成り立つ。
・分配法則は以下の通り。

（(F(x)+G(x))×H(x)=F(x)×H(x)+F(x)×G(x)も同様に導かれる）
・交換法則はRが可換であることからほぼ明らかであるので各自にゆだねる。▢

定義３
文字xに関する可換環R上の多項式F(x)=a₀+a₁x+...+aₘxᵐ+aₘ₊₁xᵐ⁺¹+...+aₙxⁿについて、aₘ≠0かつaₘ₊₁=...=aₙ=0であるときmをF(x)の次数といい、deg(F(x))と表す。ただし、deg0=－∞とする。

命題５
F(x),G(x)∈R[x]に対し次が成り立つ。
(i)deg(F(x)+G(x))≦Max{degF(x),degG(x)}
(ii)degF(x)=m, degG(x)=n（m,nは非負整数）とすると、F(x)のm次の係数aₘとG(x)のn次の係数bₙの少なくとも一方が零因子でなければdeg(F(x)×G(x))=m+nが成り立つ。

証明
(i)は+の定義から明らかである。
(ii)について、まず×の定義からdeg(F(x)×G(x))≦m+nは明らかである。F(x)×G(x)の(m+n)次の係数はaₘbₙで、aₘ≠0かつbₙ≠0であるから、aₘかbₙの一方が零因子ならばaₘbₙ≠0が成り立つ。よってdeg(F(x)×G(x))=m+n。▢

以上