
群論入門part2 群の例:対称群
※part2が投稿されたからと言ってpart3を投稿しない可能性は0ではない
※part1はこちら
※誤植や間違いがある可能性もあるため、この記事に書いてあることを過信せず、本や他の記事も参照しながら自分で考えてください。また、誤植、間違いを見つけた方はぜひお知らせください
2.1.3次対称群
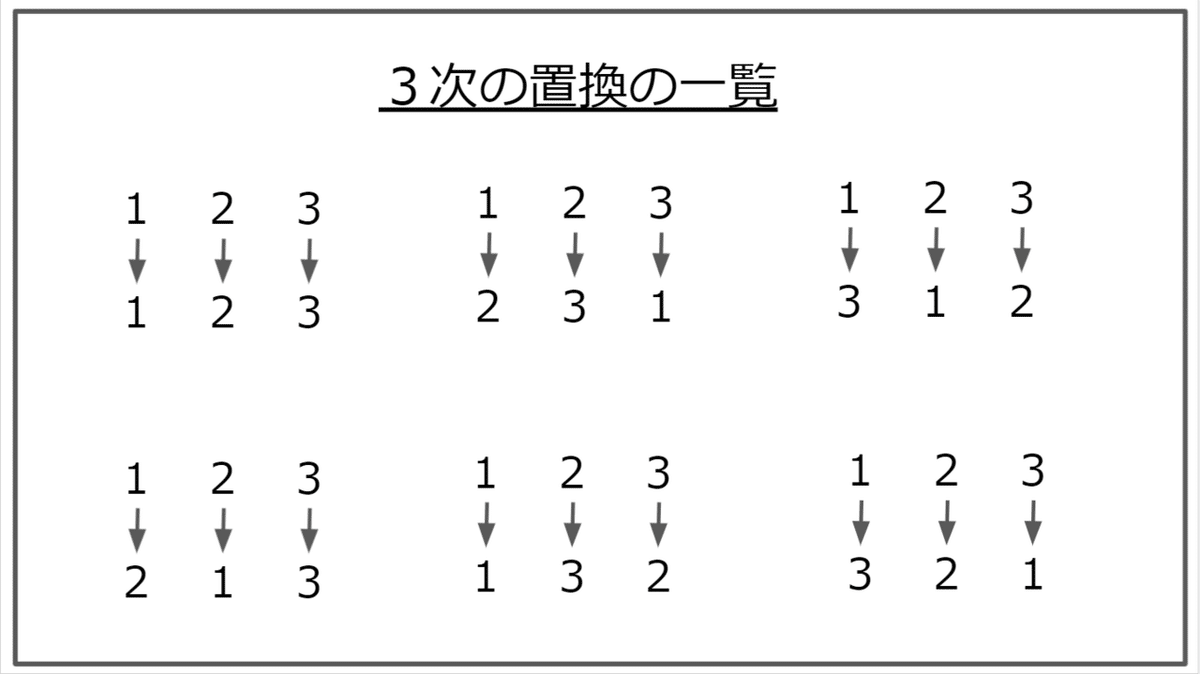
定義1(置換)
3つの自然数1, 2, 3を並べ替える操作(変換)を3次の置換という。
Rem
1, 2, 3をそのまま並び替えない操作(変換)、すなわち1, 2, 3を1, 2, 3に並び替える操作も置換である。これを恒等置換とよぶ。
Rem(少し重要)
勘違いを避けるために明言しておくが、置換というのは1, 2, 3や3, 1, 2のような数字の配列ではなく、操作(変換)そのものを指している
定義2(置換の合成)
3次の置換 u, v に対し、最初に置換 u を行い、次に置換 v を行う操作を
u・v とあらわし、これの・を置換の合成とよぶ。

Rem
2つの3次の置換を合成して得られた操作もまた3次の置換である。
命題1(単位元の存在)
恒等置換e(1, 2, 3を1, 2, 3に並び替える操作)と任意の3次の置換 σ について、σ・e=e・σ=σ が成り立つ。
(自明すぎるため証明は省略する)
命題2(逆元の存在)
3次の各置換 σ に対し、σ・δ=δ・σ=eとなる3次の置換 δ が存在する。
証明
まず、恒等置換eに対してはe自身と合成することでe・e=e。
次に1つはそのままで、ほかの2つの自然数を入れ替える置換 σに対しては、これも σ 自身と合成をすることで σ・σ=eとなる。(たとえば1, 2, 3を2, 1, 3に並び替える操作に対し、それと同じ操作を合成することで1, 2, 3↦2, 1, 3↦1, 2, 3となる)
最後にすべての自然数を入れ替える3次の置換について考える。このような3次の置換は2つあり、それぞれを δ , τ とすると、δ・τ = τ・δ =eを満たす。(各自確認せよ)▢
命題3(結合法則)
3次の置換 σ, δ, τ に対し、( σ・δ )・τ=σ・( δ・τ ) が成り立つ。
まず、命題3を証明するために次を定義する。
定義3
3次の置換 σ と1≦m≦3を満たす任意の自然数mに対し、
σにより並び替えられた自然数の配列のうち、右からm番目の自然数をσ(m)と定める。
例
1, 2, 3を2, 1, 3に並び替える3次の置換を σ とすると
σ(1)=2、σ(2)=1、σ(3)=3
命題4
3次の置換 σ, δ に対し、(σ・δ)(m)=δ(σ(m))
(証明は各自。置換の合成の定義から従う)
命題3の証明
1≦m≦3を満たす任意の自然数mに対し
(( σ・δ )・τ)(m)
=(τ(( σ・δ )(m)))
=(τ(δ(σ(m))))
=((δ・τ)(σ(m)))
=(σ・(δ・τ))(m) ▢
命題5(3次対称群)
S₃を3次の置換全体からなる集合とする。このときS₃は置換の合成をS₃上の閉じた演算とみなすことで、群をなす。ここでS₃を3次対称群とよぶ。
証明
命題1~3から従う。(群の定義を忘れた方は下の群論入門part1を参照)▢
2.2.n次対称群(ここまで理解できた人向け)
n次対称群に関しても3次対称群と同様にして構成される。特に単位元の存在と結合法則に関しては、命題1と命題3、定義3、命題4の主張および証明の中の文言の「3」を「n」に置き換えるだけでよい。
しかし、逆元の存在に関してはそうはいかない。命題2(逆元の存在)の証明では、個々の3次の置換に対して具体的に逆元を提示することで逆元の存在性を示した。
ではn次の場合はどうかというと、抽象的であり議論がしづらいというのと、n次の置換は全部でn!個(例えば6次の置換は全部で720個)あり、それらすべてに1つ1つ逆元を提示するのでは途方が暮れてしまう。
そのため別の方法で逆元の存在を示す。
※下の方法とは別に、n次対称群が群であることの簡単な証明も記事として投稿したのでぜひご覧ください。(記事のリンクはこちら)
まず、「互換」というものを定義する。
定義4(n次の置換・互換)
・n個の自然数1, 2, ..., nを並べ替える操作(変換)をn次の置換という。
・n次の置換のうち、1≦a<b≦nを満たす2つの自然数 a, bだけを交換し、その他のn-2個の自然数はそのままにする置換を互換という

Rem
1≦a<b≦nを満たす自然数 a, bだけを交換した互換を (a b) とあらわす。
定理1
任意のn次の置換は有限回の互換の合成によってあらわされる。
定理1の証明の前に例を提示する。
例
1, 2, 3を2, 3, 1に並び替える3次の置換 σ は
σ=(1 2)・(2 3)=(1 3)・(1 2)と表される。
Rem
上の例から、n次の置換の有限回の互換の合成による表し方は1通りではないことがわかる。
ではまず、定理1を示すために次の補題を考える。
補題
Sₙをn次の置換全体からなる集合とする。
n+1次の置換 δ ∈ Sₙ₊₁に対し、 δ ∈ Sₙ ⇔ δ(n+1)=n+1 と定めると
これはwell-definedである。
すなわち、Sₙ₊₁ⁿ:={δ∈Sₙ₊₁ | δ(n+1)=n+1}と定めると
f:Sₙ→Sₙ₊₁ⁿが全単射となるような写像fが存在する。
証明
f:Sₙ→Sₙ₊₁ⁿ を、f(σ)=δ と定義する。ただし、
1≦m≦nなる任意の自然数mに対し、σ(m)=δ(m)であるとする。
まず全射性について示す。
任意の δ ∈Sₙ₊₁ⁿをとると、1,2, ..., nを δ(1), δ(2), ..., δ(n) に並び替える操作はn次の置換となるため、これを σ とすればf(σ)=δ が成り立つ。よってfは全射。
次に単射性を示す。
δ=δ' となる2つの元 δ , δ' ∈Sₙ₊₁ⁿをとると、上の全射性の証明よりf(σ)=δ, f(σ')=δ' なる σ, σ' ∈Sₙ が存在する。よってfの定義から、1≦m≦nなる任意の自然数mに対し、σ(m)=δ(m)=δ'(m)=σ'(m) が成り立つため、σ=σ'。よってfは単射。▢
Rem
補題より、Sₙ ⊂ Sₙ₊₁ が任意の自然数nで成り立つことがわかる。
定理1の証明
数学的帰納法を用いて証明する。
(i) まず、1次の置換、2次の置換に関しては明らかに命題6の主張を満たすことがわかる。(ただし1次の置換については0回の互換の合成とみなして考える)
(ii) k≧2を満たす任意の自然数kに対し、k次の置換は有限回の互換の合成により表されると仮定する。この仮定の下k+1次の置換 δ に関して考える。
●上のRemから、δ(k+1)=k+1ならば δ はk次の置換とみなせるため、仮定から δ は有限回の互換の合成により表される。
●δ(k+1) ≠ k+1 の場合、δ と互換 (δ(k+1) k+1) との合成 δ・(δ(k+1) k+1)はk+1次の置換であり、(δ・(δ(k+1) k+1))(k+1)=k+1 となる。
よって δ・(δ(k+1) k+1)はk次の置換とみなせるため、仮定から
δ・(δ(k+1) k+1) は有限回の互換の合成により表される。すなわちm個の互換σ₁, σ₂, ..., σₘを用いて δ・(δ(k+1) k+1)=σ₁・σ₂・...・σₘ。
ここで(δ(k+1) k+1)・(δ(k+1) k+1)=e(恒等置換) と表されるから、上の式の両辺の右側から (δ(k+1) k+1) を合成することで
δ=σ₁・σ₂・...・σₘ・(δ(k+1) k+1) となる。よってこの場合も δ は有限回の互換の合成により表される。
以上(i), (ii)から任意の自然数nに対し、n次の置換は有限回の互換の合成で表されることが分かった▢
命題6(n次の置換の逆元)
σ₁, σ₂, ..., σₘをそれぞれ互換とすると、
n次の置換σ₁・σ₂・...・σₘの逆元はσₘ・...・σ₂・σ₁である。
証明
任意の互換 σ は σ・σ =eを満たすから、
(σ₁・σ₂・...・σₘ)・(σₘ・...・σ₂・σ₁)=σ₁・σ₂・...・σₘ・σₘ・...・σ₂・σ₁
=σ₁・σ₂・...・e・...・σ₂・σ₁
...
=e▢
Rem
定理1と命題6から、任意のn次の置換には逆元が存在することが分かった
したがって、
命題7(n次対称群)
Sₙをn次の置換全体からなる集合とする。このときSₙは置換の合成をSₙ上の閉じた演算とみなすことで、群をなす。ここでSₙをn次対称群とよぶ。
part2.1に続く...
追記
part3を投稿しました。個人的にまぎらわしいと思っている位数と位数、そして重要な群の例、巡回群についてです。
いいなと思ったら応援しよう!

