群論入門part2.1 奇置換と偶置換

※この記事は「群論入門part2 群の例：対称群」に書ききれなかった内容の記事です。

※誤植や間違いがあれば教えてください

2.3.奇置換と偶置換

そもそも置換・互換って何だ？！という方は前回の記事を見てください

前回の復習
命題１（part2の定理１）
任意のｎ次の置換は有限個の互換の積で表される。（ただしその表し方は１通りではない）

そして今回の主題
定理１
任意のｎ次の置換は奇数個の互換の積、もしくは偶数個の互換の積のいずれか一方で表される。

つまり何が言いたいかというと、置換は命題１によっていくつかの互換の積で表すことができるが、その個数が「ある時は偶数個に、またある時は奇数個になる」ことは絶対にないということを主張している。

※定理１の証明をここに書くと冗長になるため、最後に記す

例１
３次の置換はすべてで６つある。そのうち互換を除く３つの３次の置換はすべて偶数個の互換の積で表され、奇数個の置換の積では表すことができない。
たとえば１,２,３を２,３,１、３,１,２に並び替える置換をそれぞれσ、δとすると、
σ=(1 2)・(2 3)=(2 3)・(1 3)=(1 3)・(1 2)
δ=(1 2)・(1 3)=(1 3)・(2 3)=(2 3)・(1 2)
と表される。ここでこの2つの置換の右(または左)から互換をもう一つかけると、その結果は互換となってしまう。
（例：σ・(1 2)=(1 2)・(2 3)・(1 2)=(1 2)・δ=(1 2)・(1 2)・(1 3)=(1 3)）
これより、３次の置換σやδは奇数の互換の積では表すことができない。

定義２（偶置換、奇置換）
偶数個の互換の積で表すことができる置換を偶置換、奇数個の互換の積で表すことができる置換を奇置換という。

定義３
関数sgn：Sₙ→{±1}を次のように定める。
σ∈Sₙに対し、σが偶置換のときsgn(σ)=1, 奇置換のときsgn(σ)=－1
このとき、sgn(σ)をσの符号という。

Rem
定義３で登場した関数sgnは、線形代数において行列の行列式を定義する際に用いられる。行列式は大体の（特に理系の）大学生が1年生のときに習うのに対し、奇置換や偶置換は数学科とか、一部の大学生のみが習うので、筆者としてはそういう状況にある学生（僕も学生ですが）や先生を少しだけ不憫に思う。

定義４
集合Aₙ={σ∈Sₙ | sgn(σ)=1}をｎ次交代群という。
つまり、Aₙはｎ次の偶置換全体の集合である。

Rem
群論入門part3の例３、例６に登場するA₃は実は３次交代群なのであった。

命題２
ｎ次交代群AₙはSₙの部分群である。

証明
σ, δ∈Aₙのとき、σ, δはそれぞれ2k個, 2h個（k, hは非負整数）の互換の積で表される。このとき、δ⁻¹も2h個の互換の積で表される（∵part2の命題６）ため、σ・δ⁻¹は2(k+h)個の互換の積で表される。よって、σ・δ⁻¹∈Aₙ。▢
※証明には以下の事実を用いた。

2.4.定理１の証明

この節では定理１の証明をする。証明にあたっては差積という多項式や、それの派生バージョンの多項式をこねくり回しながら、最終的には「(－1)ᵐ=－1⇔mは奇数、(－1)ᵐ=1⇔mは偶数」という事実を用いて証明を完結させる。

まあこれだけだと「何を言っているのか分からん」って人が多いと思われますので1つずつ、なるべく丁寧に議論していきます。

定義５
n個の変数x₁,x₂,...,xₙからなる多項式Fᵉ(x₁,x₂,...,xₙ)を

と定義する。右辺をΠを使わないで表すと

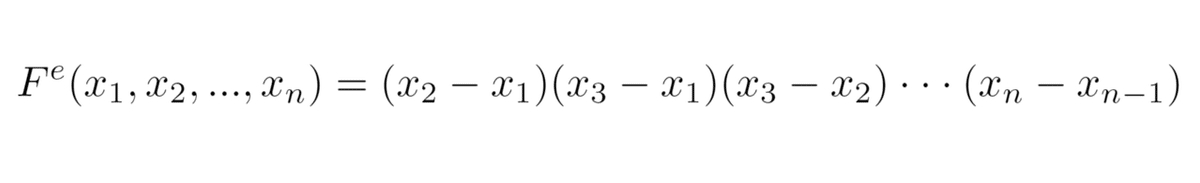
この多項式Fᵉ(x₁,x₂,...,xₙ)を差積という。

定義６
ｎ次の置換δに対し、n個の変数x₁,x₂,...,xₙからなる多項式Fᵟ(x₁,x₂,...,xₙ)を

と定義する。（δ(i)やδ(j)の定義は群論入門part2の定義３をチェック！）

Rem
FᵟをΠを使わないで表すと次のようになる

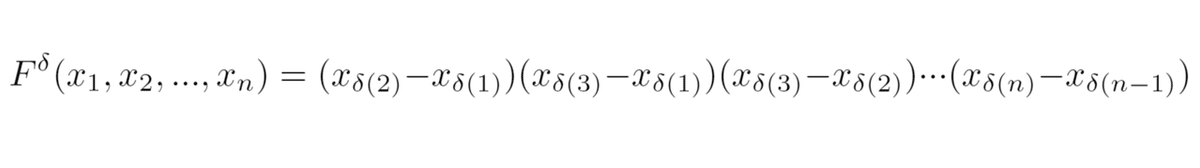
例２
Fᵉ(x₁,x₂)=x₂－x₁, Fᵉ(x₁,x₂,x₃)=(x₂－x₁)(x₃－x₁)(x₃－x₂)

例３
δ=(1 2)（1と2だけを並び替える互換）とすると、
Fᵟ(x₁,x₂)=x₁－x₂, Fᵟ(x₁,x₂,x₃)=(x₁－x₂)(x₃－x₂)(x₃－x₁)

問１
Fᵉ(x₁,x₂,x₃,x₄), Fᵟ(x₁,x₂,x₃,x₄)を求めよ。

命題３（重要）
δを互換とすると、Fᵟ(x₁,x₂,...,xₙ)=－Fᵉ(x₁,x₂,...,xₙ)が成り立つ。

証明
δ=(k h)（1≦k<h≦n）とおく。
1≦i≦h<j≦nまたは1≦i<k≦j≦nが成り立つとき、δ(i)<δ(j)を満たす。
i=k, j≠hのとき、j>hならδ(i)<δ(j)、j<hならδ(i)>δ(j)
（ここでj<hを満たす自然数jはk+1, ..., h－1までの(h－1)－k個ある）
i≠k, j=hのとき、i<kならδ(i)<δ(j)、i>kならδ(i)>δ(j)
（ここでi>kを満たす自然数iはk+1, ..., h－1までの(h－1)－k個ある）
i=k, j=hのとき, δ(i)>δ(j)

δ(i)>δ(j)となる組(i, j)の個数をmとすれば
Fᵟ(x₁,x₂,...,xₙ)=(－1)ᵐFᵉ(x₁,x₂,...,xₙ)となる。
以上より、m=((h-1)-k)+((h-1)-k)+1=2((h-1)-k)+1（奇数）となるので
Fᵟ(x₁,x₂,...,xₙ)=(－1)ᵐFᵉ(x₁,x₂,...,xₙ)=－Fᵉ(x₁,x₂,...,xₙ) ▢

命題４（命題３の派生）
δをｎ次の置換、k, hを1≦k<h≦nを満たす自然数とする。このとき、

が成り立つ

証明
命題３の証明の「i」を「δ(i)」に、「j」を「δ(j)」に、「δ(i)」を「(δ・(k h))(i)」に、「δ(j)」を「(δ・(k h))(j)」に置き換えることで、命題４の等式を得る。（つまり命題３とほぼ同じ）▢

では、定理１の証明を与える

定理１の証明
ｎ次の置換δは、命題１から（一通りではない）有限個の互換の積で表される。そこで、p個の互換β₁, β₂, ..., βₚとr個の互換γ₁, γ₂, ..., γᵣで
δ = β₁・β₂・...・βₚ = γ₁・γ₂・...・γᵣとなるものをとる。
まずδ = β₁・β₂・...・βₚであるから、命題４を適用して

この操作をあとp－1回繰り返すと、Fᵟ(x₁,x₂,...,xₙ)=(－1)ᵖFᵉ(x₁,x₂,...,xₙ)。
次にδ = γ₁・γ₂・...・γᵣであるから、上と同様に議論することで
Fᵟ(x₁,x₂,...,xₙ)=(－1)ʳFᵉ(x₁,x₂,...,xₙ)が成り立つ。よって、
β₁・β₂・...・βₚ = γ₁・γ₂・...・γᵣならば
(－1)ᵖFᵉ(x₁,x₂,...,xₙ)=(－1)ʳFᵉ(x₁,x₂,...,xₙ)が成り立つ。ここでFᵉ(x₁,x₂,...,xₙ)に関して特に制約はないので、Fᵉ(x₁,x₂,...,xₙ)=0であるとは限らない。
すなわち、(－1)ᵖ=(－1)ʳが成り立つため、pとrの偶奇は一致する。これより、定理１が証明された。▢

以上