
【高校情報1】ハフマン法・ランレングス法(可逆圧縮法)と非可逆圧縮
◆◆はじめに◆◆
文部科学省:高等学校情報科「情報1」教員研修用教材
第2章 コミュニケーションと情報デザイン
学習6 ハフマン法・ランレングス法(可逆圧縮法)と非可逆圧縮 抜粋
高等学校情報科「情報Ⅰ」教員研修用教材(本編):文部科学省
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm
学習6について、一気に作成する予定でしたが、ハフマン法とランレングス法についての解説が長くなったので、まずは、その部分を切り出して動画作成しました。
情報Ⅰ共通テスト対策 書籍出版します!
◆◆動画解説◆◆
◆◆文字おこし◆◆
ファイルの圧縮方法について説明していくね。

文書ファイルなどは,圧縮したものを完全に元に戻す必要があるよね。
このような圧縮方法を可逆圧縮といい,ランレングス法やハフマン法などがある。
画像,音声,動画などのファイルは,完全に元に戻す必要がない場合もある。
このような圧縮方法を非可逆圧縮といい,可逆圧縮に比べて圧縮率をあげることができる場合が多い。

ランレングス法の圧縮方法について説明していくね。
例えば,AAAAABBBBB という連続した文字列がある場合,最初の文字列と連続する個数を記録することにすれば,A5B5 のように表現される。このように10 文字分が4 文字分で表現されるので,ファイルは元の40% に圧縮されたことになる
ただ、ラングレス法には欠点がある。
たとえばABCDEという文字列があった場合は、同じ方法で圧縮すると
A1B1C1D1E1というふうに5文字だったのが10文字に増えて圧縮したら、元のファイルより容量が大きくなってしまう。
つまり、ラングレス法は連続する同じ値が多い場合に有効な圧縮方法なんだ。

FAX などは文字も図形もモノクロの画像として送受信される、さっきのランレングス法で考えるとA を白い部分,B を黒い部分と考えれば,白が続く部分や黒が続く部分がかなりあるため,ファイルは相当程度圧縮することができる。

次に、ハフマン法について見ていこう。
「intelligence」という文字列で考えていくね。
intelligenceは、intelgc の7種類の文字でできているよね。7種類の文字を2進法で表すには3ビット必要だね。もう少し説明すると、1ビットは2の1乗で2種類、2ビットは2の2乗で4種類、3ビットは2の3乗で8種類まで表すことができる。
つまりintelligenceについていえば1文字を3ビットで表現可能だから12文字×3ビットで36ビットのデータ量が必要になる。
ここで,文字に割り当てるビット数を減らせば,
あまり使われない文字のビット数を増やしても全体のデータ量を減らすことができる。このような考え方で行う圧縮の方法をハフマン法という。

具体的にやっていくね。
まずは,「intelligence」という文字列における文字の出現回数を割り出す。
iは2回、nは2回、tは1回、eは3回、lは2回、gは1回、cは1回となる
そしてこれを、出現回数の多い順に並び替えて、出現回数の多い文字に対して少ないビット数の符号を割り当てる。
例えばintの文字列部分でみると101100となる。
1がi 、01がn、100がt という感じになる。本来は3ビット×3で9ビットなのが6ビットまで圧縮できた感じになる。
ただ、これだけだと区切りが分からないから、区切る位置によっては101のg 、100のtと読めたりもする。
どこで区切られるかということが分かる、ハフマン木というものを作成して、それと組み合わせて確認する必要がある。

少しややこしいけど、順を追って詳しく説明していくね。
まずは文字の出現回数順に並べる。これはさっきやった内容とおなじ。
そして、出現回数の少ない方から、gとcの出現回数を合計して、その上に合計値を記入する。この場合はg,c共に1回づつだから合計は2となるね。
つぎにlとtも同じように2+1で3を上に記述する。つぎにiとnは2+2で4を上に記述する。eは同列のペアがいないから、一つ前に計算したiとnの合計値にたいしてeの出現回数をプラスする。
右に戻って今度はgとeの合計値である2と、lとtの合計値である3を足した5を上に記述する。
最後に7と5をプラスして、12がピラミットの頂点となる。
つなぎ合わせたすべての部分の左に0を、右に1を入れていく。
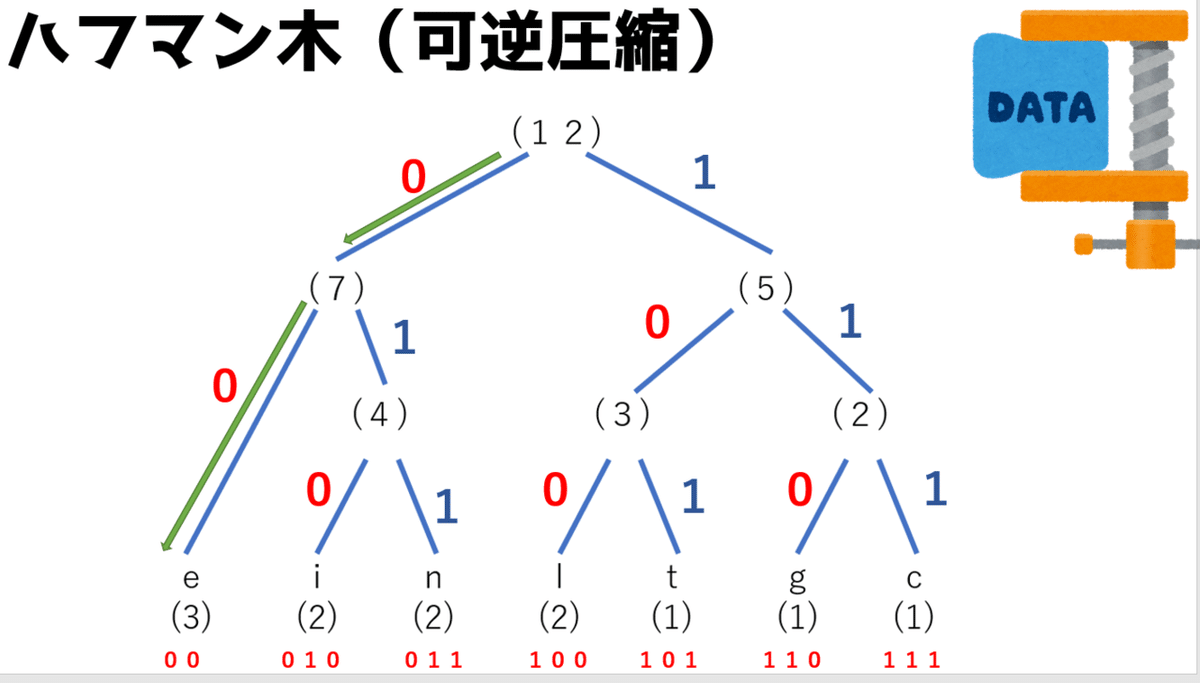
そして、つなぎ合わせた部分に入れた0と1を上から拾っていく。
eの場合は00、iの場合は010、nの場合は011という感じで、それぞれの文字に圧縮したビット列を割り当てる。
例えば、圧縮したビット列「00」があったとすると,0と1を上からたどれば対応する文字は「e」だけとなる。
「100」を上からたどれば対応する文字は「l」となる。
このような方法で各文字に割り当てる符号を定め,これを基に圧縮する方法をハフマン法という。

ハフマン法では,常に各文字列に対応するハフマン符号の表と,それを基に圧縮されたビット列をセットでファイルに格納することになる。
例えば、作成したハフマン符号を用いて「intelligence」を圧縮したビット列で表すと,
「010(i) 011(n) 101(t) 00(e) 100(l) 100(l) 010(i) 110(g) 00(e) 011(n) 111(c) 00(e)」のように33 ビットとなる。
「intelligence」の1文字を3 ビットで表していた場合は36 ビットだったから,約92% に圧縮されたことになる。
実際には,これに各文字列に対応するハフマン符号の表がつくので圧縮率はこれより低くなる。ただ,ある程度長い文章であれば,出現頻度の高い文字に少ないビット数の符号が割り当てられるから,文書全体のデータ量に比べてハフマン符号の表のデータ量が小さくなるので,ランレングス法より高い圧縮率が期待できるんだ。
ハフマン法はややこしかったと思うけど、違う文字列で自分自身の手で練習すればすぐに覚えられると思うよ。
