
【高校情報1】シミュレーション/確定モデル・確率モデル 円周率とモンテカルロ法 Pythonプログラミング/教員研修用教材 学習16
◆◆はじめに◆◆
第3章 コンピュータとプログラミング
学習16 学習モデル(確定モデルと確率モデル)モンテカルロ法と円周率
https://www.mext.go.jp/a_menu/shotou/zyouhou/detail/1416756.htm
別動画でアップしているPython超入門講座は一通り理解している前提で進めています。教員研修用教材に完全に準拠した形で解説しています。
Pythonプログラミングで必要な内容は、学習15までで全て網羅できている(グラフを読み解く能力の方が必要)と感じていたため、流して簡易に説明しようと思っていたのですが、2点引っかかる点があったのでそこは詳しく説明しています。
情報Ⅰ共通テスト対策 書籍出版します!
1.配列について
以下のプログラムのコメントでいきなり「配列」という言葉が出てきました。「リスト」の説明は研修用教材内で詳しくありましたが、「配列」の説明はどこにもありません。

一応、型をtype(yokin)で出力したら、リスト型でした。
Pythonプログラムは、配列型もあるので、型として配列と言っているなら狭義には間違っているのではと感じました。
広義には、配列型とLIST型を合わせて「配列」と言っている場合が多いので、型としての違いを補足的に説明しています。

2.モンテカルロ法と円周率
教員研修用教材では

という文言があります。
20回読み返しても、訳が分からない・・・
半日かけて色々調べて、
モンテカルロ法と円周率とPythonを用いたシミュレーションの関係性を、中学生が分かるレベルまで掘り下げて動画にしました。

正直、数学の先生じゃないと「円周率×モンテカルロ法とは」をわかりやすく教えられるひと少ないんじゃないかな・・
でも、プログラミングは情報の先生・・
数学科の先生と情報科の先生がコラボですかね(^^)
それか、両方できる賢者的な先生(あっ!E.V.ジュニアさん)
◆◆動画解説◆◆
◆◆文字おこし◆◆
今日は確定モデルと確率モデルについて学んでPythonでプログラミングしてシミュレーションをしていこう。
事物や現象の本質的な形状や法則性を抽象化して,より単純化したものを「モデル」という。
そして、事物や現象のモデルを作ることをモデル化という。
このモデルを使って、実際には行う事が困難な実験を計算だけで行なったり,複雑な現象を再現したりするための手段としても活用できたりする。

モデルは,対象の特性や表現形式によって分類することができる。
表現形式のモデルは、縮尺モデル、数式モデル、図的モデル等に分類される。
対象の特性のモデルは大きく静的モデルと動的モデルに分類される。
静的モデルは,例えばプラスチックモデルや建築図面などのように時間的要素を含まないものなんだ。
一方、動的モデルはレジの待ち行列や,気象予測,生物の成長など,時間的要素を含んだ事象のモデルなんだ。
更に、動的モデルは確定モデルと確率モデルに分類される。
確定モデルは不規則な現象を含まず,方程式などで表せるモデルで
確率モデルはサイコロやクジ引きのような不規則な現象を含んだモデルなんだ。
じゃあ、確定モデルのシミュレーションをしていこう。

複利法による預金金額の時間的変化を考えてみよう。
複利法は元金に利息を加算し,それを次の期間の元金として利息を計算していく方法なんだ。
●複利法の数式モデル は次の計算式で表される。
次期の金額=現在の金額+利息
利息=現在の金額×利率×時間間隔
# 預金の複利計算のプログラム
yokin = 100000
riritsu = 0.05
for i in range(10):
risoku = yokin * riritsu
yokin = yokin + risoku
print(i+1, " 年目:", yokin)10年間の預金変化をPythonのプログラムで表そう。
一番初めに預け入れる金額は10万としてyokin変数に代入。
年利は5%として、0.05をriritsu変数に代入する。
後は10年分求めるから、ループを10回 回すようにfor文のrangeの中は10とする。
ループの中でその年の利息を求めて
預金利息に加えて。
年数と共に預金額を表示する。
実行してみよう。
5%の利率の場合には9年ほどで1.5倍になることがわかるね。

じゃあ今度は、これをグラフで表してみよう。
グラフは以前Pythonの超入門講座のライブラリの回で説明した
matplotlibを使う。
もし、まだインストールしていなければ、Python超入門講座を確認してmatplotlibをインストールしてね。
――――――
以前、複数の箱を格納できるLIST型について説明したけど、広義では配列と言ったりする。

厳密に言うと
Pythonでは
LIST型と配列型がある
LIST型は、要素数が可変で違う型のデータも格納することができる。
配列型は、要素数をはじめに定義して変更は不可、同じ型のデータのみ格納できる。
広義には、どちらも配列と言ったりするし、
大学入学テストの疑似言語の問題では配列という表現が使われるから、
今回はlist型も配列と呼ぶね。
------------------------------------------------------------------
# 預金の複利計算をしてグラフを表示するプログラム
import matplotlib.pyplot as plt
riritsu = 0.05
yokin = [100000]
for i in range(10):
risoku = int(yokin[i] * riritsu)
yokin.append(yokin[i] + risoku)
plt.title("FUKURI KEISAN")
plt.xlabel("Year")
plt.ylabel("Yokin[YEN]")
plt.plot(yokin, marker="o")
plt.show()
まず、matplotlibの機能群をpltという名前でインポートする。
最後にグラフに纏めて表示するために、預金変数はリスト型の配列として定義する。
そしてfor文の中で10年分の計算結果をyokin配列に格納する。
グラフタイトルをFUKURI KEISAN
X軸ラベルをYear
Y軸ラベルを Yokin[YEN]
として、預金配列を受け渡し、グラフを表示する。

実行してみよう。
ちゃんと折れ線グラフでグラフが表示されたね。
―――
こんどは、確率モデルのシミュレーションをしていこう。

6面体のサイコロは各面積が等しく,振り方に偏りが無ければ,目の出方は各面が6分の1の確率で出現するはずだよね。
乱数を発生させて、サイコロを100回振ったシミュレーションをしていこう。
さっきと同じようにmatplotlibを使ってサイコロの各目が何回出たかを棒グラフで表示するPythonプログラムを組んでいくね。
# 6面体のサイコロを100回振った目の出方のシミュレーション
import numpy as np
import numpy.random as rd
import matplotlib.pyplot as plt
saikoro = rd.randint(1, 6 + 1, 2000)
deme = [] # 出目の数を数える配列
for i in range(6):
deme.append(np.count_nonzero(saikoro == i + 1)) # 数を数えて配列に追加
left = [1, 2, 3, 4, 5, 6]
plt.title("SAIKORO SIMULATION")
plt.xlabel("ME")
plt.ylabel("KAISUU")
plt.bar(left, deme, align="center")
plt.show()数値計算で用いられる、numpy(ナムパイ)というライブラリをnpという名前でインポートする。
numpyはAI,機械学習領域でもよく用いられているんだ。
そして、乱数を発生させる機能の呼び出しも行う。
次に6面体のサイコロを100回振るという処理を再現する。
これは1以上、6+1未満の乱数を発生させ、小数点以下を切り捨てて1から6の整数を算出し、100回繰り返した値を、saikoroの変数に入れている。
出た目を数える配列をdemeという変数で定義して
次のfor文でサイコロの目毎に数を数えてdemeの配列に順番に格納している。
これをグラフに出力する処理を記述していこう。
まず、グラフの左方向の値を1~6までの整数で定義する。
そして、グラフタイトル、xとy軸ラベルを定義し。
算出した値を渡してあげて、グラフを表示する。
実行してみよう。
◆◆ライブラリエラーになった場合◆◆
エラーになったね。
numpyは外部ライブラリだから別にインストールが必要なんだ。
コマンドプロンプトを立ちあげて
pip install numpy
と入れてエンターキーを押そう。
そうしたらインストールが始まる。
インストールがおわったら、もう一度プログラムを実行してみよう。
◆◆

各目が何回現れたかが棒グラフで表示されたね。グラフを見る限り今回の100回だとばらつきがみられるよね。
試行回数を2000回にしてみよう。

100回の時に比べて、各目の出方のばらつきが小さくなったことが分かるね。
確率モデルを使ったシミュレーション手法に,モンテカルロ法がある。モンテカルロ法の特徴は対象のモデルに乱数を大量に生成して入力し,近似解を得ようとする手法なんだ
分かりずらいと思うから、円周率の例で説明していくね。

まず、円周率は円の直径に対する円周の長さの比率のことなんだ。
そして、円の面積は 円周率×半径の2乗 だったよね。
公式で1表すと円の面積をS 半径をr 円周率をπとした場合
S=πr2乗だね。
だから、半径を1とした場合 π×1×1=πとなり。
円周率と円の面積とがイコールとなるんだ。

円の中心をX軸 Y軸共に0とした場合
円の上の部分は Xは0 Yは1 円の右側は Xは1 Yは0となる。
右斜め上はXは1 Yも1 となる。
その4点を結ぶと、長さが1の正方形が描ける。
つぎに、その正方形の中にランダムに点を打っていく
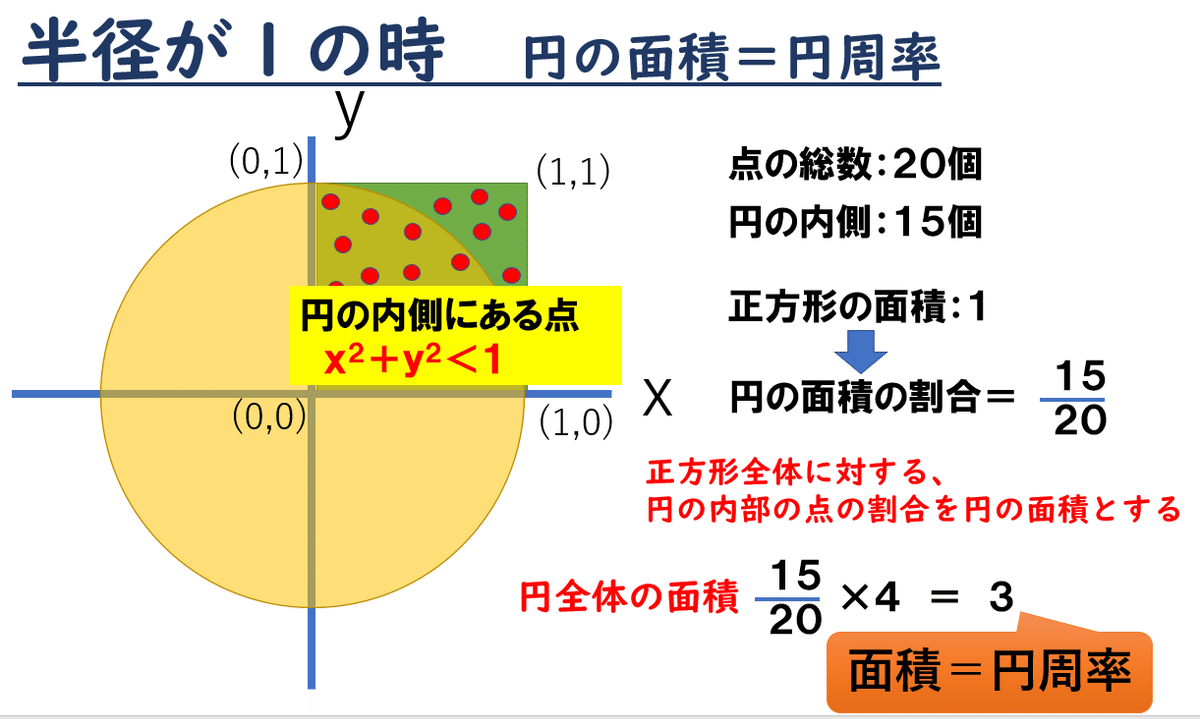
とりあえず、20個ランダムに点を打つね。
その打った点について、円の内部に存在する点を数える。
今回は20このうち 15個が円の内側に入ったとする。
正方形の面積は1×1で1だよね。
その面積に対して、均等に点が打たれたとした場合、
円の面積は 20分の15で表される
つまり、正方形全体に対する、円の内部の点の割合を円の面積として考えるんだ。
今回は円全体に対する面積の4分の1の面積を求めたわけだから。
これを4倍すれば円全体の面積となる。
そして、はじめに話したように、半径1の円の面積が円周率と一致するから、
今回の場合は
20分の15 ×4 が円周率となる。
さっきのサイコロと同じように点の数を増やすほど、精度が上がり、皆が知っている3.1415の円周率に近づいていく。
ちなみに、点が円の内部にあるかどうかは置いた点のxとyの座標を確認して
xの2乗プラスyの2乗の値が1より小さければ、円の内側となる。
つまりxの2乗プラスyの2乗が1の場合は点が円周上に位置しているんだ。
import numpy.random as rd
import matplotlib.pyplot as plt
totalcount = 2000 # ランダムに打つ点の総数
incount = 0 # 円に入った点の数
for i in range(totalcount):
x = rd.random() # 0-1 の範囲の値
y = rd.random() # 0-1 の範囲の値
if x**2 + y**2 < 1.0:
incount += 1
plt.scatter(x, y, c="red") # 赤色の点(円内部)
else:
plt.scatter(x, y, c="blue") # 青色(円外部)
print(" 円周率:", incount * 4.0 / totalcount) # 円周率
plt.title("Monte Carlo method")
plt.show()今話した内容をPythonプログラムで表すとこんな感じになる。
今回は点を2000個打っていこう。
円の中に入った点を赤と円の外だった点を青にして、円周率を求めるプログラムを組んでいこう。
numpy(ナムパイ)とmatplotlibの呼び出しはさっきと同じ
ランダムに打つ点の総数を2000としてtotalcount変数に代入する。
円に入った点の数は初期値0としてincountに代入する。
for文はtotalcount数だから2000回繰り返す
さっきのx2乗プラスyの2乗が1より小さい場合は
円の中に入ったってことだから、赤色で点をうつ、それ以外は青にする。
同時に、円の内側の点の数÷打った点の総数 ×4をしてさっき説明したように円周率も出力してみよう。

青と赤に分かれて円の4分の1が描かれて、同時に今回の半径1の場合の円の面積つまり円周率が算出できたね。
さっき話したように打つ点が多くなるほど精度が上がって3.1415・・のみんなの知っている円周率に近づいていく。
こんな感じでランダムな数を沢山与えて、事象を確率的に解析することをモンテカルロ法というんだ。
大学入学共通テストでは、このシミュレーションした結果を複数組み合わせて読み解く能力が求められるから、今後問題演習を通して、データ解析能力を鍛えていく予定だよ。
