
MYP-Math-数の起源を探究-
サニーサイドインターナショナルスクールの中等部で「MYPの原則から実践へ(リンク)」を参考にしながら数学の授業実践をしています。また、授業でしようしている教材は「MYP Mathematics1 by Oxford」をベースにしながら、授業のデザインをしています。
数学科の目標としてカリキュラムコーディネーターの方から伝えられたこと。参考となる動画はこちらです。
「世の中を数学的に見ることができる人を育成すること」
まずは、MYPの数学の枠組みにある、4つの学習分野の1つである「数」の探究からスタートしました。
「なぜ、私たちは数を学ぶのか?」
生徒は、数を用いてパターンを表現したり、実生活の状況を描写したりする行為の起源は人類が最初に出現した時期にまでさかのぼるという事実や、数学が多文化的な起源をもつという事実を理解する必要があります。
私たちは、数学と聞くと「どこか難しい」と感じてしまい、数学の持つ利便性よりも公式を覚えることや公式を当てはめて問題を解くことに難しさを感じて実生活の様々な状況を描写するのに数学が用いられている価値に気づかないまま数学を学んできたように思えます。
そこで、今私たちが学んでいる数の概念がない世界を世界を想像するところからUnit1の学習をスタートしました。
Unit1のカリキュラム内容
こちらが、Unit1のカリキュラムの概要になります。
【探究テーマ】
文明が進化し、人間が相互作用するにつれて、さまざまなシステムと表現の形式が発達する。
【重要概念】形式
【関連概念】表現、システム
【グローバルな文脈】文明と人間の相互作用
【事実的問い】
・数とは何か?
・数の体系とは何か?
【概念的問い】
・数量を表現する方法はどのように影響されたのか?
・数量の表現方法は有用性にどのように影響しているのか?
【議論的問い】
・過去の出来事は私たちにどのような影響を与えているのか?
【評価基準】パターンの探究
探究の流れ
具体的な探究の流れはこちらです。
【導入】
> 現代当たり前にある数の概念の重要性を学ぶ
【展開①】
> 身の回りにある数の概念の起源を紐解く
・円周と円の面積を古代使用されていた方法で解く
・バビロニア時代の0進法を紐解く
【展開②】
> 身の回りの数のパターンを紐解く
・素数の探究
・倍数のパターンの探究
・最小公倍数/最大公約数をユークリッド法で解く
【形成的評価】
> 2進数の仕組みを探究
【総括的評価】
> 古代数学の仕組みを探究
導入

導入では、紀元前約4000年前にシュメール人が数と数え方を使用していた記録が残っていることから、今当たり前に私たちが使用している10進法の考え方や数の表記方法を使わずに様々な量の動物の数を友達に伝え合うワークを行いました。少ない数であれば、動物の絵を書いて伝えることができたのですが100を超えるあたりから数の位取りのシステムの重要性に気づき始めていました。
こういうワークを通して数や数のシステムの重要性や人間が生活の中で数を使用し、相互作用しながら数のシステムが発展してきているのを学んでいきます。
展開①

最初の展開では、子どもたちにとって馴染み深い円周の求め方を考える学習からスタートしました。今私たちは当たり前のように円周の公式は「直径×3.14」を用いて求めると思いますが、そもそもこの人類の叡智とも言える円の公式はどのようにして発見されてきたのかを考えていきました。
「円周の公式を用いずに、どのようにして円周の長さを求めますか?」
最初は使用できるものとして、紐を用いて子どもたちは円周の長さを測っていました。そして、このユニットの評価基準でもある「パターンの探究」を観点に「円の直径と円周にはどのような関係があるのか?」という問いを投げかけ、子どもたちは直径と円周の関係性について紐を使って調査を始めました。他にもモンテカルロ法や古代エジプトのパピルスの紙に書かれた方法等様々な方法で円周率を求める探究を行いました。
こういうワークを通して今私たちが当たり前に使っている公式が、長い時間をかけて相互作用しながら発見されてきたことと、自分たちでも公式を覚えて当てはめて使うだけの学びではなく、パターンを発見するスキルを磨いていきます。
展開②
次の展開では、小学校の算数で学ぶ、倍数のパターンを発見する学習を行いました。数字を見て、倍数を見分ける方法は、最近では塾等で見分け方を学ぶと思うのですが、子どもたちは数字をたくさん並べてパターンを発見する力を持っていました。ここに数学の授業だからこそ育める力があります。
複数の実例から共通項をまとめることによって、事実を導き出し一般化させる(=数学的帰納法)
子どもたちが発見したのは、テキストに書かれてある綺麗に一般化されているものではありません。しかし、子どもたちは数字を書き出し、並べ替えたり、四則演算したり、自分が知っている様々な方法を使って法則を導き出していました。そして、クラスの中で発見した様々な法則が相互作用しながら、授業の中で一般化の質が高まっていく動きも見られました。
形成的評価

形成的評価では、これまでに学習してきたパターンを発見するスキルを応用させて、二進法のシステムを説明する学習を行いました。
私たちは当たり前のように10進法を使っているからこそ、異なるシステムである2進法の説明ができない時、感覚で10進法の位取り法の考え方を理解していたことに気づくと思います。
また、頭で理解するのは難しくても実際に四則演算の計算を通して、2進法の理解が進んだ生徒もいました。10進法と2進法が掴めると、他の進法の理解も進み、1-12進法でカレンダーをつくるワークも行いました。

総括的評価
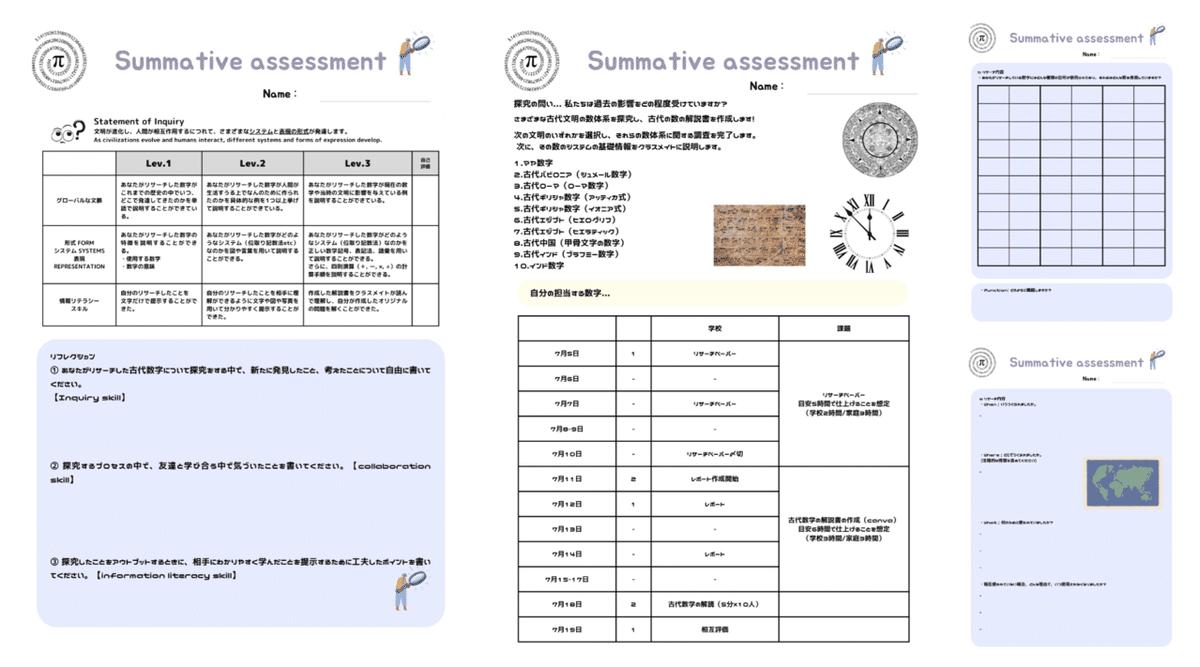
総括的評価では、形成的評価でフォーカスしたスキルと考え方を活用して、古代数学を解明する解説書とクイズ(kahoot)を作成する課題を出しました。
▽ 解明する古代の数学
1.マヤ数字
2.古代バビロニア(シュメール数字)
3.古代ローマ(ローマ数字)
4.古代ギリシャ数字(アッティカ式)
5.古代ギリシャ数字(イオニア式)
6.古代エジプト(ヒエログリフ)
7.古代エジプト(ヒエラティック)
8.古代中国(甲骨文字の数字)
9.古代インド(ブラフミー数字)
10.インド数字
参考文献
子どもたちは、異なる数のシステムを理解するだけでなく、異なる数の表現方法の解明を行い、最終プレゼンテーションでは相手が理解できる解説書とクイズの作成を行いました。

生徒は、古代数学の解明の探究に関心を示しており、10人で10個の古代数学の解明を行うことができました。また、10人で探究するからこそ、1つの事例では見えてこない、複数の事例を見ることで、探究のメッセージである「文明が進化し、人間が相互作用するにつれて、さまざまなシステムと表現の形式が発達する」ことを理解できたのではないかなと思います。また、クラスの文脈でもパターンを発見するプロセスの中で、クラスメイトでの相互作用のやり取りの中で一般化のレベルが上がる瞬間も印象的な瞬間でした。
参考文献
1. MYPの原則から実践へ(リンク)
2. 「数学」指導の手引き(リンク)
次回のレポートでは、Unit2の内容をまとめていきます。ここまで読んで頂きありがとうございます。
