
基本 Tableauの計算について
Tableauでは、「集計」と「非集計」の違いを理解し、適切に活用することがとても大切です。今回は、その違いを詳しく解説します。また、自身の勉強のためにも、基本的な関数についても解説していますので、ぜひ参考にしてください。
データ:サンプルスーパーストア
集計と非集計
Tableauではデータの「集計」と「非集計」があります。
簡単に説明すると以下の通りです。
集計メジャー
データをまとめて集計する事ができます。
売上合計(SUM):すべての売上を足し合わせた金額
平均値(AVG):すべての売上の平均額
最大値(MAX):最も高い売上
最小値(MIN):最も低い売上
非集計メジャー
通常、売上を行へドラッグ&ドロップすると、自動的に合計として集計されますが、非集計で分析をしたい場合は▼ボタンから「ディメンション」を選択すると、集計されず一つずつの数値として表すこととができます。

非集計ディメンション
データをそのまま表示します。
顧客名 :各注文を行った顧客の名前
オーダーID:各注文の識別番号
例えば
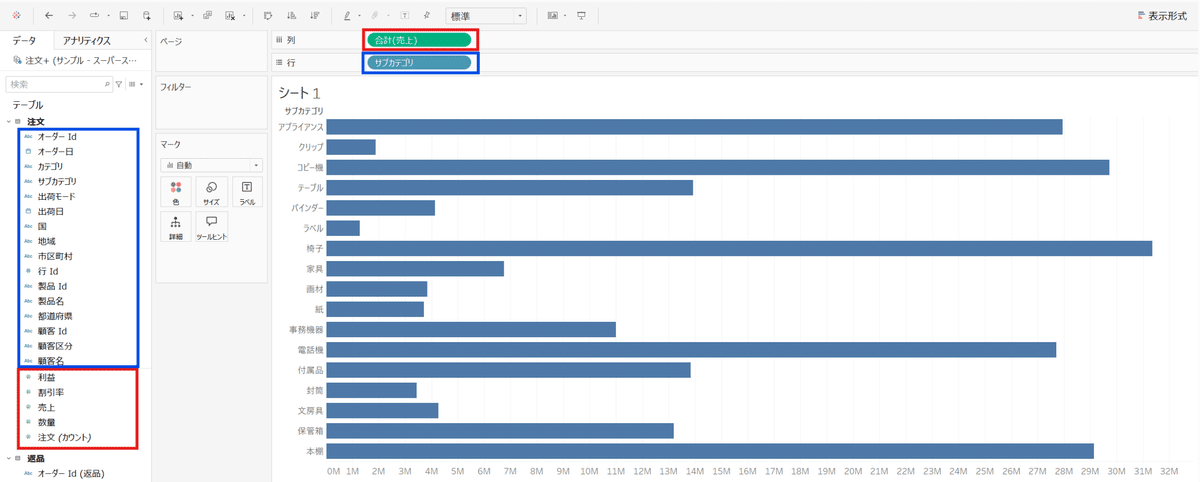
列へ売上 行へサブカテゴリ ドラック&ドロップします。
売上であるメジャーの値は、ビューに追加した場合自動で「合計」となり集計されます。
またディメンションであるサブカテゴリはそのまま表示されます。
集計ディメンション
カウント、カウント (個別) を使用して、ディメンションを集計することができます。
サブカテゴリをテキストへドラック&ドロップします。
カウント(サブカテゴリ)、個別のカウント(サブカテゴリ)一つずつ表示します。

カウント :重複も含め、データの数を集計します。
カウント(個別):重複をの除いて、データの数を集計します。
例えば
ディメンションである「カテゴリ」を以下のように集計する事ができます。
サンプルスーパーストアに入っているサブカテゴリの行Idのカウントは、全部で10000件。個別のカウントでは、重複除いて集計されている事が分かります。

計算の集計と非集計
集計
すべての「利益」の合計をすべての「売上」の合計で割る計算です。

非集計
各行で計算した後に各行の結果を合計します。

行Idが行レベルで集計されているため、集計と非集計の計算結果は同じとなっています。

次に地域のディメンションでビューの粒度で見てみます。
集計
関西地方で集計された利益と集計された売上を割ったものが計算されている
非集計
データの行単位で計算されて合計されている

このようにTableauで計算を扱う際は、集計、非集計の考え方が重要です。
関数について
論理関数
都道府県ごとに利益率がある
その利益率が何%以上か分岐させて色分けしたい場合
論理関数で表すことができる
利益率(集計):SUM([利益])/SUM([売上])

IF [利益率(集計)]>0.25 THEN"Good"
ELSEIF [利益率(集計)]>0.08 THEN"OK"
ELSE"Not Good"
END
もし利益率が25%より大きかったら”Good”
それ以外の場合で利益率が8%より大きいとき”OK”
それ以外の時は”Not Good”
出来上がったものを色へドラック&ドロップする。

ドリルダウンしてみます。
顧客区分を列へ入れると、都道府県と顧客区分ごとに利益率が表示されます。都道府県毎に集計された利益を集計された売上で割っています。

日付関数
日付の計算を行うときに使用する、日付の差を計算します。
出荷モード別に
オーダー日から実際に出荷された日数がどれくらいだったか比較したい場合
DATEDIFF("day",[オーダー日],[出荷日])
オーダー日から出荷日の差を日付単位で取得したいので
"day"を使用
週単位なら”week”となる

列に追加します。

合計ではなく平均へ変更します。

即日なら直ぐ出荷されている事が分かりました。

文字列関数(分割)
顧客名を苗字と名前を分割する場合
顧客名の▼を右クリックし「変換」「カスタム分割」を選択する。

区切り文字の使用「半角スペース」
分割は全てにすれば「前」「後」すべて取得できます。

顧客名-分割済み1,2ができました。

文字列関数(連結)
カテゴリ、サブカテゴリ、製品名 つなげて表示したい場合
[カテゴリ]+"/"+[サブカテゴリ]+[製品名]

計算フィールドの使用方法
今回は基本的な操作についてお伝えしましたが、計算フィールドの作成のウィンドウでは関数に関して検索出来る場所があります。
例えば「日付」に関する関数を作成したい場合、日付を選択すると
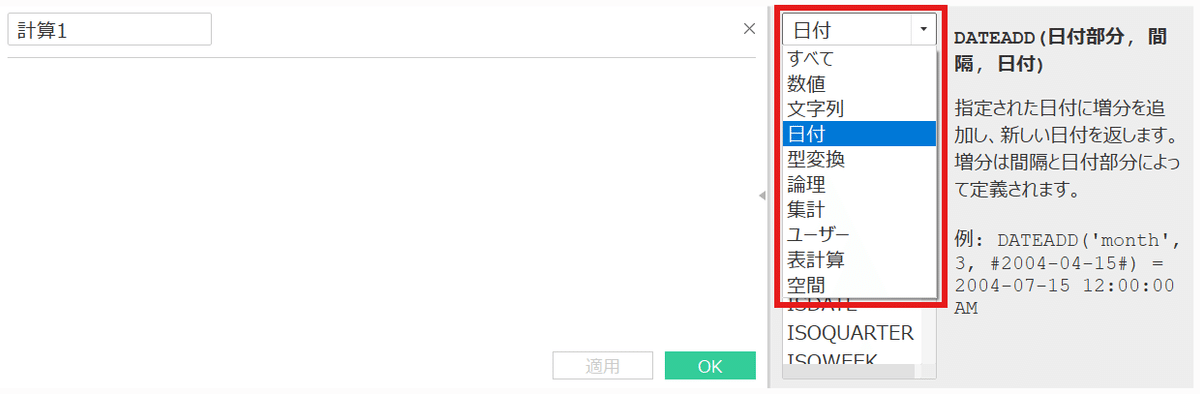
日付に関する関数が表示され、関数を選択すると右側に説明と例が表示されます。

関数を忘れても何となく導き出してくれます。
関数って難しいけど、なんとなく出来るような気がしませんか♪
