
数学 Project note#5【数学B】短歌や俳句はなぜ5・7・5?
テスト・受験のためだけの教科書”を”教える授業からの脱却を目指し、高校数学のプロジェクト学習を紹介する記事です。お気づきなことがあればご指摘いただければ幸いです。
0.はじめに ~150年前は…~
生徒に、こんな話をします。
問題1「150年前のスマホはどんなものだったでしょうか?」

生徒「トトロでみたことある!」
生徒「近所の人の家で電話かけてたヤツ!」
問題2「150年前の車はどんなものだったでしょうか?」

生徒「馬車!」(正解!)
問題3「150年前の学校はどんなものだったでしょうか?」

画像:Youtube
「学校システムを告訴する」I JUST SUED THE SCHOOL SYSTEM より
https://www.youtube.com/watch?v=dqTTojTija8
時代に応じて教育もカタチを変えていくべき。変わってはいけないものもあるけど、変わらないといけないものもある。
問題4「では、何を変えていくべきだと思う?どんな教育がいいと思う?」
色々意見を聞いた後、最後に私はこの言葉を紹介します。

(車が存在する前に)客に何が欲しいかを聞くと、「早い馬がほしい」というだろう。ヘンリー・フォード
スティーブ・ジョブズはこんな言葉を残しています。

だから、これからの教育を一緒に築きたい。
少なくとも「テスト直前に暗記して、テスト後には忘れてしまう、テストや受験のためだけに勉強する数学は変えていくべき。」と述べています。
1.数列とは
「なぜ、短歌や俳句は、5・7・5なの?」
この問いが、今回の最も大きな問いです。5と7が並ぶ「数列」と呼ぶこともできます。
数列というと難しいですが、普段から数列にはお世話になってます。
例1)時刻表(等差数列)

「等差数列」・・・隣同士の差が一定の数列のこと。
一定の差を「公差d」とよび、時刻表の公差d=5とd=8では、バスの来る頻度が変わります。
例2)音階

「等比数列」・・・隣同士の比率が一定の数列のこと。
ドレミファソラシドの隣り同士には、周波数が×106倍の関係性があります。音楽業界では、1つ音階が上がることを「半音上がる」と言いますが、数学的には誤りで、数学的には「等倍上がる」あるいは、「周波数が×1.06倍上がる」というべきです。
2.フィボナッチ数列とは
問題 ▢に入る数字は?

このような、「1つ前と2つ前足して、次の数になる」数列を「フィボナッチ数列」と呼びます。ここで驚くべきことは、隣同士の比率がある値に近づいていくのです。(隣同士の比率が一定のものは等比数列(前述))
②番目÷①番目 1÷1=1
③番目÷②番目 2÷1=2
④番目÷③番目 3÷2=1.5
⑤番目÷④番目 5÷3=1.666…
⑥番目÷⑤番目 8÷5=1.6
⑦番目÷⑥番目 13÷8=1.625
・・・(繰り返していくと)・・・
比率=1.6180339…
になっていきます。この比率は「黄金比」とよばれる比率で、この比率で作られたものは「美しくみえる魔法の比率」です。
3.黄金比とは



アートや建築物、花びらの数(生徒の発表の資料)にも表れる、美しくみえる魔法の比率です。
4.白銀比とは
西欧の人が好むとされる「黄金比(1:1.6180339…)」に比べ、日本人が好きとされる「白銀比(1:√2 = 1 : 1.414213…)」があります。


神社仏閣、A4用紙のサイズ、日本のキャラクターに使われたりします。(キティ―ちゃんが日本のキャラクターとは知らない人も多いですが…)くまモンに至っては「黄金比」「白銀比」が両方使われています。
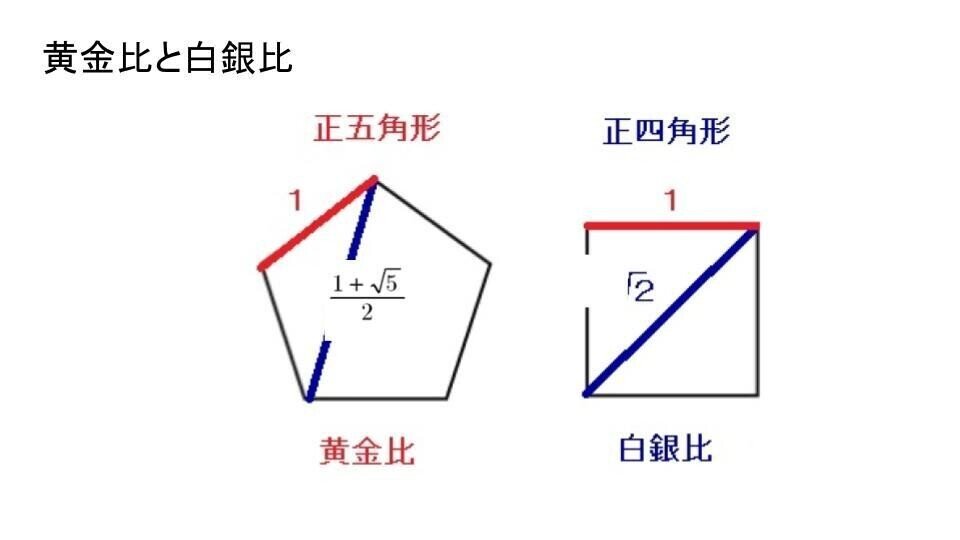
ちなみに、覚えにくい方のために、
「黄金比(1:1.6180339…)」・・・1辺が1の正五角形の対角線の長さ
「白銀比( 1 : 1.414213…)」・・・1辺が1の正方形の対角線の長さ
になります。
5.「なぜ、短歌や俳句は、5・7・5なの?」

ここから著者の仮説ですが、日本人が好む「白銀比( 1:√2 = 1 : 1.414213…)」は整数比にすると、「5:7」。まさに日本人が好む美し割合だったのです。「4:7」や「5:6」では日本人にとっては美しくないなんですよね。
ここで一つ、問いを広げてみましょう。
6.短歌・俳句を黄金比で作ってみると…

「黄金比(1:1.6180339…)」の整数比は「5:8」、「5:8」で詠んでもいい歌が歌えるのではないか、というのが数学的な見方です。(国語的には不適切かもしれません、あくまで数学的な見解です)
さらに、フィボナッチ数列の隣り同士の比率は「黄金比」なので、フィボナッチ数列である、「3:5:8:13:21…」で詠んでも美しくなるのではないでしょうか?ぜひ、黄金比でも歌を詠んでみてください。

いかがでしょう?5・7・5ではないけど、いいリズムのような気がしませんか?
その後、みんなで歌を詠んで楽しみました。
最後まで読んで頂きありがとうございます。ワクワクする数学教育の一助になれば幸いです。
いいなと思ったら応援しよう!

