数学 Project note#4【数学全般】別解掲示板

テスト・受験のためだけの教科書”を”教える授業からの脱却を目指し、高校数学のプロジェクト学習を紹介する記事です。お気づきなことがあればご指摘いただければ幸いです。

０．はじめに　～数学をなぜ学ぶのか～

「数学をなぜ学ぶのか？」
そんな話も生徒と行います。
・受験のため
・テストでいい点とるため
・社会で役に立つため
・思考力をつけるため　etc...

だいたい生徒から出てくる言葉そんなところだと思います。どれも正しいと思います。私もテストのための勉強を全否定しません。テストの効果で数学を好きになる、解くことが楽しくなる効果もあると思うからです。

「社会で役にたつ」「思考力をつける」これらの言葉がより具体化して卒業できる生徒を輩出したいですね。そのために私も悪戦苦闘しています。

さて、文科省はこのように３つにまとめて述べています。

①陶冶的な意義（とうや）
②実用的な意義
③文化的な意義

今回の「別解掲示板プロジェクト」は、
「多角的な視点や知的好奇心を身に付ける」の①陶冶的意義
「複数の見方を楽しむ」の③文化的な意義
の狙いで進めました。

１．ルール（第Ⅰ期）

（BP：別解ポイントのこと）
対称：３年生の入試対策のクラス
スライドを共同編集にして、全員がスライドに掲載できるようにしています。山﨑が別解が考えられる問題を掲載しましたが、自分で問題を掲載する生徒も後に少し現れました。

２．別解例（第Ⅰ期）

ピンクの附箋は、山﨑からのフィードバック

例１）「判別式を使う方法（数Ⅰ）」と「解と係数を使う方法（数Ⅱ）」
まさに、３年生になったからこそ、１・２年生で学んだことを結び付けて考察できる。

例２）
Ａさんが「①点と直線の距離（数Ⅱ）」と「②三角関数（数Ⅱ）」
Ｂさんが加えて「③ベクトルの内積（数Ｂ）」「④積分（数Ⅲ）」「⑤コーシーシュワルツの不等式（高校では学ばない）」
合計５つの解法を２人の生徒で導いた。クラスメイトとの思考のキャッチボールのようで、数学者にとっては見ていて楽しい。

例３）
「式の計算で解く（代数的）」「図形で解く（幾何的）」
私はよく代数は左脳（計算）で考え、幾何は右脳（視覚）で考えると表現しますが、脳をフル回転させて考察しているといえる。

例４）
あえて面倒な方法をとることで「別解の価値」や、「複数の解法を考える意義」に気づいてくれると信じて…。

３．別解例（第Ⅱ期）

第Ⅱ期は、第Ⅰ期のルールに加えて、「証明でもよい」「他者の解答にフィードバックする」を設定しました。

例１）
普段当たり前のように使う公式も、「なぜ？」を見直すいい機会になる。

例２）
生徒のコメントも加わり、対話的に学ぶ。

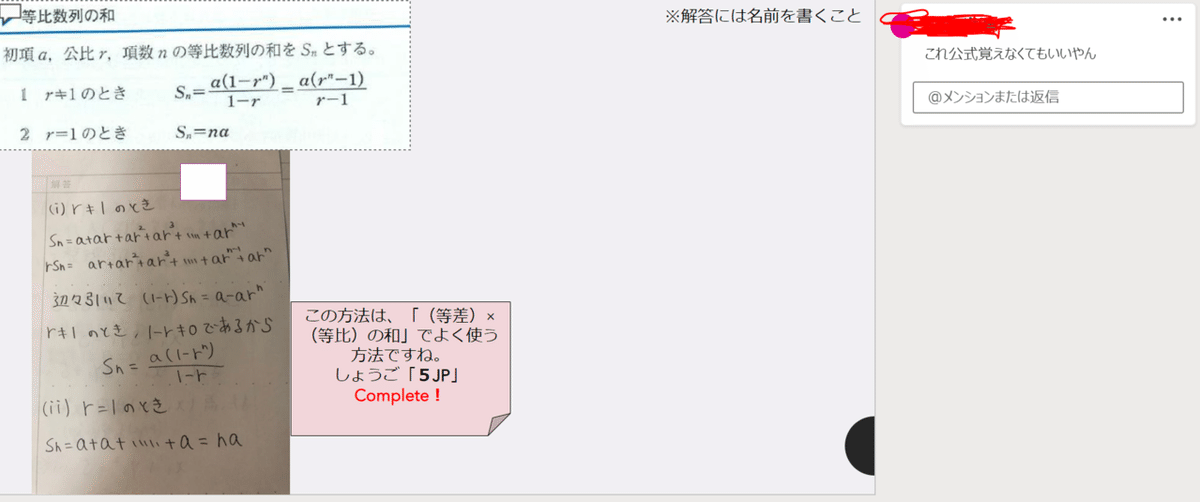
例３）
別の見方を教師がガイドすることも当然必要です。（青い附箋は山﨑）

例４）
証明に穴があれば、指摘するだけでなく、クラスで共有することが大切。（黄色い附箋は教師）

４．「三平方の定理」証明シリーズ

ある生徒が面白がって、数学で最も大切な公式の１つ「三平方の定理（中学数学）」の証明をたくさん解いてきたので紹介する。

証明①）もっともメジャーな方法。中学校の教科書もこれ。

証明②）相似を使った方法

証明③）等積変形を使った方法
このあと、余弦定理の証明も同様にできることを話すと、この生徒は嬉しそうに解いてきました。

証明⑤）内接円を用いた方法。高校数学が使われる。

証明⑥）方べきの定理を使った方法。（数学A）
中学の内容を高校数学の視点から見つめる機会になった。

証明⑦）「方べきの定理」（数学A）

証明⑧）台形の面積

証明⑨）面積比

証明⑩）無限等比級数（数学Ⅲ）
他の生徒も、数Ⅲで勉強したこととの繋がりを感じる証明。

５．最後に

私が数学の楽しいと感じるときは、
①難しい問題が解けたとき
②社会の事象を数学的に見たり考えたりできたとき
③別の解法が見つかったとき

少しでも生徒もその楽しさを味わってもらえたらと願う。

最後まで読んで頂きありがとうございます。ワクワクする数学教育の一助になれば幸いです。