
「Pythonではじめるオープンエンドな進化的アルゴリズム」の付録サンプルを動かしてNEAT-Pythonに入門してみる
最近購入した書籍「Pythonではじめるオープンエンドな進化的アルゴリズム」の付録サンプルコードを動かしながら勉強したことの備忘メモです。
#Python #進化的アルゴリズム #強化学習 #機械学習 #勉強記録
目次
概要
遺伝的アルゴリズムのおさらい
NEATアルゴリズム
書籍付録のクッキー探しゲーム
感想
参考資料
(補足)追記済のコード
概要
強化学習を触り始めたころから遺伝的アルゴリズムなどの進化的アルゴリズムの分野には興味を持っていましたが、
いざ勉強しようと思って本を探すと大学の教科書みたいな難しそうな本しかなく取り掛かれていませんでした。
ところが最近オライリーから下記の本が出版されていることを知りました。
私が普段から触り慣れているPythonと絡めて勉強できそうで、なにより面白そうだったので即買いしました。
岡瑞起, 斎藤拓己, 嶋田健志 Pythonではじめるオープンエンドな進化的アルゴリズム - 発散型の機械学習による多様な解の探索
書籍の付録サイトに記載されているサンプルコードがボリュームが小さいわりに面白く、ぜひ紹介したいと思い本メモを書きました。
遺伝的アルゴリズムのおさらい
遺伝的アルゴリズムの大まかな流れとキーとなる処理(選択・交叉・突然変異)について書籍の概要図(下図: Pythonではじめるオープンエンドな進化的アルゴリズム p17図2-1より引用)を交え簡単におさらいします。

遺伝的アルゴリズムでは問題の解を「遺伝子」(ベクトル)として表現して次の世代に進化させることで最適解を探索します。
書籍記載の内容に加え、こちらの解説も大変わかりやすく参考にさせていただきました。
k8o - 遺伝的アルゴリズムについてコードも交えて説明する
個体と適応度
書籍の例にならい各個体をコーヒー、遺伝子(※)をその淹れ方、適応度を美味しさの指標値(0-100)として下記の通り表します。
※左から順に豆の種類を表す数値, 豆の量, 粉の粗さを表す数値, 水温, 抽出方法を表す数値, 抽出時間
個体A: [1, 20g, 7, 93℃, 1, 45s] (適応度 95)
個体B: [2, 18g, 5, 90℃, 2, 50s] (適応度 75)
個体C: [3, 10g, 2, 80℃, 3, 10s] (適応度 25)
まずは解きたい問題を上記のような遺伝子と適応度の形に落とし込むことが必要で、ここを上手に行うのが現実の問題に遺伝的アルゴリズムを活用する際の最初のハードルになりそうです。
選択
個体群の中から主に適応度を用いて次の世代へ残す優秀な個体を選択する操作です。
いろいろな方法があるようですが、単純に適応度の高いものを残す方法(ランキング選択)がシンプルで採用されることが多いとのことです。
上記の例だと個体A, B(⇔おいしいコーヒー)が適応度が高く次世代へ引き継がれる可能性が高いです。
交叉
選択された個体同士を掛け合わせて次世代の個体を生成する操作です。
これも色々な方法があり、書籍内では1点交叉が例として紹介されていました。
上記の参考にさせていただいたサイトによると、1点交叉は効率が悪く現在はほぼ使われておらず2点交叉が使われることが多いとのことです。
例えば個体A,個体Bを2点交叉( | を交叉ポイントとする)させたとすると
個体A: [1, 20g, | 7, 93℃, 1, | 45s]
個体B: [2, 18g, | 5, 90℃, 2, | 50s]
↓
個体D: [1, 20g, 5, 90℃, 2, 45s]
のような個体Dが生成されることになります。
ちょうどA, Bのいいところを併せ持つおいしいコーヒーができるかも?しれませんし逆の結果になるかもしれません。。。
突然変異
個体の遺伝子を一定確率でランダムに変更させる操作です。
この操作を行いすぎるとただ単にランダムに次世代を生み出してるだけになってしまうので高すぎるとよくない様子。
通常、突然変異が発生する確率は0.1~1%程度に設定するのがベターと参考資料の中には書かれていました。
上記の操作を所定の終了条件に達するまで繰り返し行い、最終世代の最も優秀な個体を解とします。
NEATアルゴリズム
NEAT(NeuroEvolution of Augmenting Topologies)はNNの構造を下図のようにノード遺伝子とコネクション遺伝子として表現し、より良いNNへ進化させていく手法です。2002年に下記リンクの論文にて提唱された手法です。
Kenneth O.Stanley, Risto Miikkulainen - Evolving Neural Networks through Augmenting Topologies
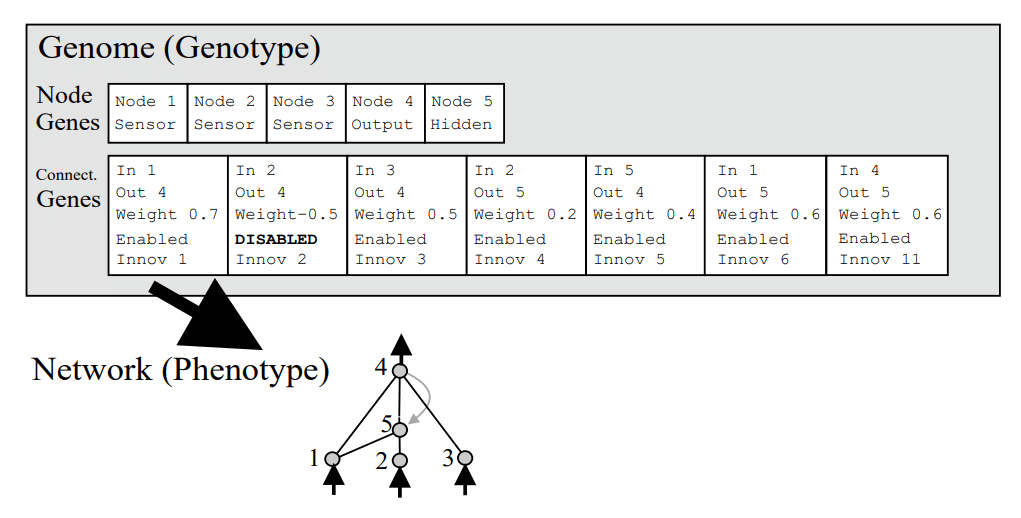
おおざっぱに遺伝的アルゴリズムと対応させると、
ある問題に対するNNを「個体」、その構造を「遺伝子」、NNの出力から得られる評価値が「適応度」のイメージですかね。
よくこんなことを思いついたなーと感心するばかりです。
大まかな流れは遺伝的アルゴリズムとほぼ同じですが、種分化や競合緩和など新たな概念も追加されていてすごく面白いです。
(下記は Pythonではじめるオープンエンドな進化的アルゴリズム p29より引用)
初期集団を生成
種分化
集団の個体を評価
選択、交叉、突然変異により新たに集団を生成
2~4を繰り返す
元論文や今回購入した書籍、もっと詳しくわかりやすい解説サイト様などがありますのでNEATの各操作の説明は簡潔に飛ばします\(^o^)/
突然変異(NEAT)
ネットワークの構造や重みをランダムに変更します。
主な突然変異には、重みの微調整、ノードの追加、接続の追加や削除などがあります。
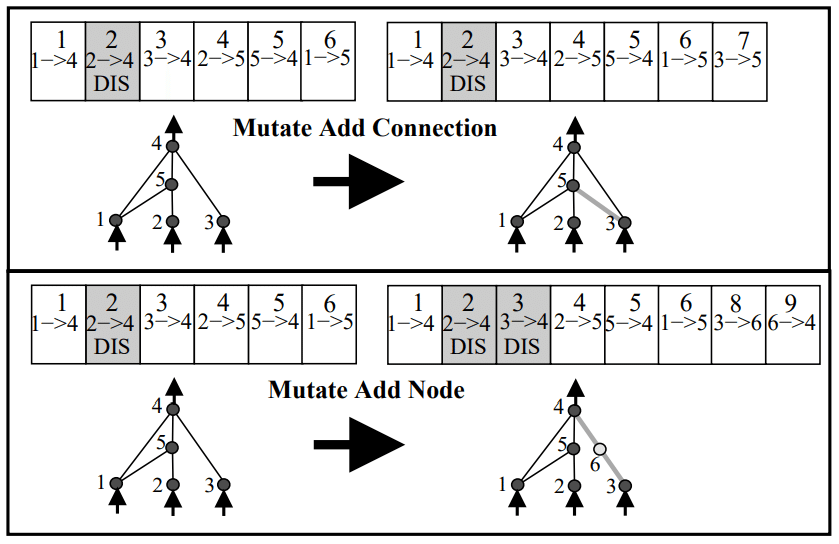
交叉(NEAT)
親のネットワークの構造や重みを部分的に交換することで親の良い特徴を引き継ぎつつ新しいネットワークを生成します。

種分化と競合緩和(NEAT)
私が一番面白い&すごいなーと思った考え方がこの種分化の考え方です。
NN間の距離δを定義して近いNN同士⇔似た種族に分割してその種族内で競争させるイメージ。
これにより多様性を確保し、局所解にトラップされることを防ぐ効果があるみたいです。

距離の定義は上式の通りで(各値の意味は論文参照ください)、neat-Python中でNN間距離を算出している箇所の一部はこのあたりのコードのようです。
(処理の細かい部分まで追えていないです。。。)
競合緩和は下記のように種族内の適応度の平均が高い種族の個体数を増やすように種族の大きさを決定させる考え方です。
種族1: [n=50, 平均適応度=0.4] -> [n=25 (-25)]
種族2: [n=30, 平均適応度=0.8] -> [n=50 (+20)]
種族3: [n=20, 平均適応度=0.4] -> [n=25 (+5)]
このように種族の大きさもある程度制御することで、異なる種が競り合いながらも進化を続けられるようになるようです。
書籍付録のクッキー探しゲーム
いよいよ今回購入した書籍の付録コードを動かしてみます。
付録1 NEAT-Pythonの使い方の理解を深める
動かす前の準備
windowsの場合はneat-pythonとともに
pip install neat-python windows-cursesでwindows-cursesをインストールしておきます。
絵文字とstdscr.addchを使用している部分を修正すれば無事動きました。
VSCodeのターミナル上でちゃんと表示されました。(やや文字化け?のような表示が残るが気にしない)
windows用に追記修正したコードは本メモの末尾に添付しておきます。
処理の流れ
p = Population(c)であらかじめ記述しておいたconfigファイルの内容に基づいて初期集団生成
各個体についてコード内のforループ内の処理を行い適応値を得る
大まかなルールは下記の通り。
・i(移動回数カウント), x, y(それぞれエージェントの現在位置)の3つをNNに入力し出力o_xy[0],o_xy[1]を得る
・下記ルールに従いエージェントを移動させる
axis = 0 if o_xy[0] > o_xy[1] else 1
amount = 1 if o_xy[axis] < 0.5 else -1
if (current[axis] + amount) > 1:
current[axis] += amount
・iが規定値を超えてもゴールにたどり着かなかった場合はその時のゴールとの距離 * (-1)を適応値とする
・ゴールにたどり着いた場合は適応値を+1000とするconfigファイルの内容に基づき種分化、選択、交叉、突然変異させて次集団生成
(2,3を繰り返し)
NNの出力をエージェントの行動に変換するルールの部分はなぜこの式になっているのか?が私の不勉強もありよく理解できませんでした。
初期位置が[30, 80]でゴールが[10, 10]なのでマイナス方向の移動が採択されやすい形にしたのかなとは思うのですが。。。
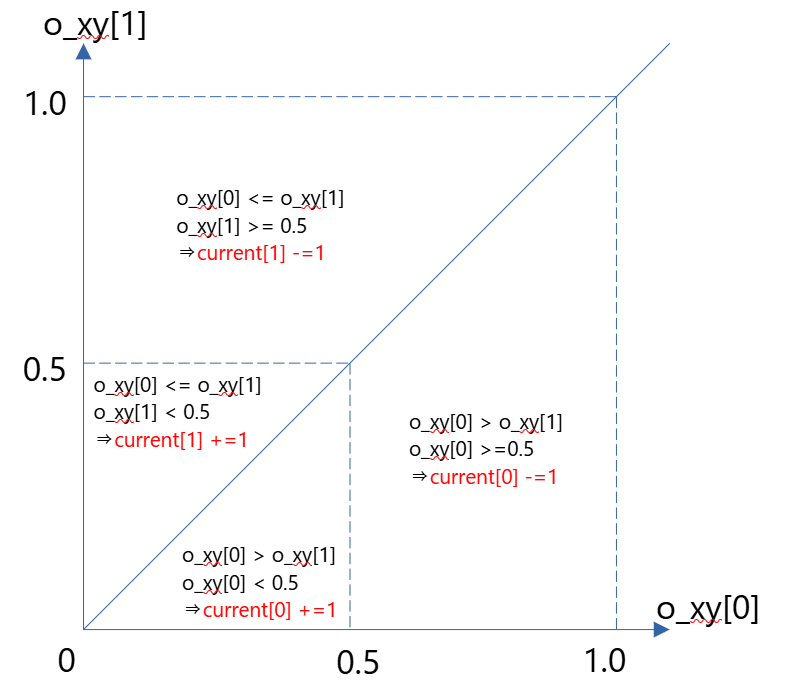
configファイル
こちらで公式ドキュメントを日本語で詳しく解説されており、大変助かりました。
toI fromI - NEAT-Pythonの公式ドキュメントを見ながら少しずつ読んでいく(2)
ここを確認すればconfigの中身はおおよそわかると思います。
[NEAT]
fitness_criterion = max
fitness_threshold = 100
pop_size = 10
reset_on_extinction = False
no_fitness_termination= False
[DefaultGenome]
# network parameters
num_inputs = 3
num_hidden = 1
num_outputs = 2
feed_forward = True
initial_connection = partial_direct 0.5
# node activation options
activation_default = sigmoid
activation_mutate_rate = 0.0
activation_options = sigmoid
# node aggregation options
aggregation_default = sum
aggregation_mutate_rate = 0.0
aggregation_options = sum
# connection add/remove rates
conn_add_prob = 0.5
conn_delete_prob = 0.5
# node add/remove rates
node_add_prob = 0.2
node_delete_prob = 0.2
# connection enable options
enabled_default = True
enabled_mutate_rate = 0.01
# node bias options
bias_init_mean = 0.0
bias_init_stdev = 1.0
bias_max_value = 30.0
bias_min_value = -30.0
bias_mutate_power = 0.5
bias_mutate_rate = 0.7
bias_replace_rate = 0.1
# node response options
response_init_mean = 1.0
response_init_stdev = 0.0
response_max_value = 30.0
response_min_value = -30.0
response_mutate_power = 0.0
response_mutate_rate = 0.0
response_replace_rate = 0.0
# connection weight options
weight_init_mean = 0.0
weight_init_stdev = 1.0
weight_max_value = 30
weight_min_value = -30
weight_mutate_power = 0.5
weight_mutate_rate = 0.8
weight_replace_rate = 0.1
# genome compatibility options
compatibility_disjoint_coefficient = 1.0
compatibility_weight_coefficient = 0.5
[DefaultSpeciesSet]
compatibility_threshold = 3.3
[DefaultStagnation]
species_fitness_func = max
max_stagnation = 100
species_elitism = 1
[DefaultReproduction]
elitism = 2
survival_threshold = 0.1
min_species_size = 2実行結果
VSCode上のターミナルで実行しました。
ターミナル画面上をエージェントが[10, 10]のクッキーを探して走り回ってくれて面白いです。
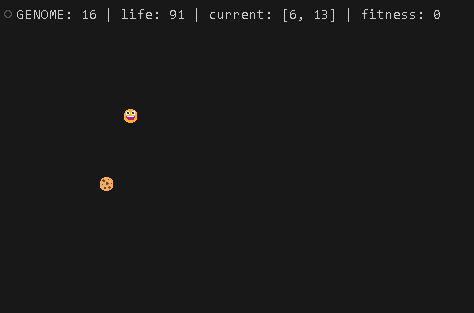
最後に最優秀個体winnerがp.run()の返り値として得られます。

比較的運よく早めの世代でゴールにたどり着いた際の結果例です。
入力ノードは-1, -2, -3で出力ノードは0, 1で、突然変異により隠れ層に11, 15のノードが生成されていることがわかります。(が、出力ノードには接続されていないようです)
下記2行をコード末尾に追記して、生成された種族の数と最優秀個体はどの種族に属していたのか?も確認してみました。
print(p.species.species)
print(p.species.genome_to_species)上記の例だと種族ID=1, 2の2つの種族が発生し、今回の最優秀個体(key=27)は種族1に属していることがわかります。
感想
頭のいい人たちが考えることはすごいなぁ^p^(小並感)
いままでどちらかというと機械学習(強化学習)寄りの分野を触ることが多かったので、
数理最適化・メタヒューリスティクスの分野が弱いなぁと感じていました。
今回ようやく一歩踏み出せた感があります。
まだ本の前半部分(2章まで)しか読めてませんが3章以降も大変面白そうです。
・・が、めっちゃ難しそうです。
少しずつ勉強しつつ、実際にこれを何かに応用できるようなテーマも探していきたいです。
(実際に使って動かしてみないとちゃんと理解できないですよねー・・・)
参考資料
岡瑞起, 斎藤拓己, 嶋田健志 Pythonではじめるオープンエンドな進化的アルゴリズム - 発散型の機械学習による多様な解の探索
Kenneth O.Stanley, Risto Miikkulainen - Evolving Neural Networks through Augmenting Topologies
コード(追記済)
from neat.config import Config
from neat.genes import DefaultNodeGene
from neat.genome import DefaultGenome
from neat.population import Population
from neat.reproduction import DefaultReproduction
from neat.species import DefaultSpeciesSet
from neat.stagnation import DefaultStagnation
from neat.nn import FeedForwardNetwork
from pathlib import Path
import os
import curses
import itertools
import math
import time
def eval_genomes(genomes, config, foo):
for genome_id, genome in genomes:
net = FeedForwardNetwork.create(genome, config)
# ================ ドメインに依存する処理を実装する ==========
genome.fitness = 0
BLANK = " "
GOAL = "\U0001F36A"
AGENT = "\U0001F600" # エージェントの生成
GAME_CLEAR = "\U0001F60D"
GAME_OVER = "\U0001F47D"
goal = [10, 10] # ゴール (この場所を探す)
current = [30, 80] # エージェントの開始位置
stdscr = curses.initscr() # 画面の初期化
stdscr.addstr(goal[0], goal[1], GOAL) # ゴール
for i in itertools.count():
# 表示を更新
stdscr.addstr(0, 0, f"GENOME: {genome.key} | life: {i} | current: {current} | fitness: {genome.fitness} ")
if goal == current: # ゴールに到達
genome.fitness += 1000 # 報酬を追加
stdscr.addstr(0, 0, f"GENOME: {genome.key} | life: {i} | current: {current} | fitness: {genome.fitness} ")
stdscr.addstr(current[0], current[1], GAME_CLEAR)
stdscr.refresh()
time.sleep(5)
break
if i > 100: # 寿命に到達
# ゴールと自分自身の距離を測る
distance = math.sqrt(
(goal[0] - current[0]) ** 2 + (goal[1] - current[1]) ** 2
)
genome.fitness -= distance # 報酬を追加
# ゲームオーバー
try:
stdscr.addstr(0, 0, f"GENOME: {genome.key} | life: {i} | current: {current} | fitness: {genome.fitness} ")
stdscr.addstr(current[0], current[1], GAME_OVER)
stdscr.refresh()
time.sleep(0.3)
stdscr.addstr(current[0], current[1], BLANK)
except curses.error: # 画面はみ出し(文字だけ表示)
stdscr.addstr(1, 1, "DEAD")
stdscr.refresh()
time.sleep(0.3)
stdscr.addstr(1, 1, " ")
stdscr.refresh()
break
try:
# エージェント描画
stdscr.addstr(current[0], current[1], AGENT)
stdscr.refresh()
time.sleep(0.01)
stdscr.addstr(current[0], current[1], BLANK)
except curses.error:
pass # 画面はみ出し(無視する)
# 移動
input_data = [
i,
current[0], # 現在位置
current[1], # 現在位置
]
o_xy = net.activate(input_data)
axis = 0 if o_xy[0] > o_xy[1] else 1
amount = 1 if o_xy[axis] < 0.5 else -1
stdscr.refresh()
if (current[axis] + amount) > 1:
current[axis] += amount
# ================ ドメインに依存する処理ここまで ===========
def main():
# 実行ファイルと同じ場所にsimple.confを置いておく
conf_file = Path(os.path.dirname(__file__)) / 'simple.conf'
c = Config(
DefaultGenome,
DefaultReproduction,
DefaultSpeciesSet,
DefaultStagnation,
conf_file,
)
p = Population(c)
winner = p.run(eval_genomes, n=100) # 10世代
curses.endwin() # ゲーム画面の終了
print(winner)
print('--------------------------------------------------------------------')
print(p.species.species)
print(p.species.genome_to_species)
if __name__ == "__main__":
main()
