東大物理2021を実況する（その２）

　以前の記事東大物理2021を実況する（その１）をご覧になっていない方は，そちらからご覧下さい。第２問は第１問とは打って変わって，来年以降の受験生向けの試験場での実践的な話が中心になりそうです。最後までお付き合いいただけたら幸いです🙇‍♂️

　問題はこちら。（配点予想はあくまで予想です。全体の出来不出来によっても左右される可能性があります→開示返却後、少し訂正を入れました）

第２問：コンデンサー回路と振動回路

　第１問は面積速度一定の式も与えられており，[やや易]～[標準]難易度でしたが，こちらは先程よりも難しそうですね。図を見ただけでも極板がゴチャゴチャしそう，コイルまである。って感じで計算もキツそうです😫

設問Ⅰ：⑶まで見渡すと，エネルギーの話が主体になってるのがわかるので，コンデンサーの極板間引力をエネルギー保存で考える典型問題かなぁ🤔と思いながら解いていきました。（今回は引力の大きさまでは問われませんでした）

⑴：まずはコンデンサーの電気容量です。答えだけをシュンカンで答えて終わりですね。原理からわかっていればシュンカンなのですが，試験場では案外ド忘れしてしまうのかもしれません😥

　それにしても，2019年の電磁気の最初の問題と同じ出題でしたが，もしかして2019年のとき割と出来が悪かったんですかね🤔？（実際そうだったらしいと、後から先輩にお聞きしました）そんなことを頭の片隅で考えながら⑵へ向かいます。

⑵：電気容量の値から，電荷，そして静電エネルギーを求めます。まぁ特にひっかかるところはないですね。この時点で⑶でエネルギー保存に関する設問がありそうだなぁと考えたりします。

　ここで一瞬止まるとしたら，極板Aと極板Cを導線でつないだら電荷分布どうなるねん？ってことですね。案外，この辺で詰まってしまうのかもしれません。経験の有無は試験場の瞬発力にかなり影響すると思います。（2013(後期)東北大（以下画像）などがほぼそのまんまですね）

⑶：電池が繋がれているタイプのエネルギー保存ですね。基本的に電荷の移動に目を向けて，静電エネルギーの変化ΔUを導入して終わりです。ここも特に迷うところはありません。電池が負の仕事をすることがあることもジョーシキですね。

　解答速報などではむやみやたらと答えの式を通分したりして，綺麗にしていますが試験場では時間の無駄ですね。答えが同値なら何でも丸です。答えの形の綺麗さなんて求めてないでさっさと次に進みます😤。ちなみに何倍かと問われていますが，ここで分子分母を間違えてー1/2倍と説明なしで書いたりしたら目も当てられないので，W/W0のように書いて安全を取りました。

　ここまではコンデンサーの極板に着目したミクロな現象を扱ったので，問題で与えられた図からここからは回路全体に目線を向ける（マクロな視点）での問題がきそうだなと見当をつけて，設問Ⅱに進みます。（ここまでで８分）

　予想配点は⑴１点，⑵２点，⑶W：２点，W/W0：２点くらいでしょうか（⑴は2019にも出題があるため、配点は低そう。）

設問Ⅱ：ここからはコンデンサー回路の問題です。これも予想通りでした。というのも，近年，2006，2011，2016とmod 5で1となる年は基本的に回路の問題が出題されており，現役生への配慮及び2019の出題（交流回路の本格的な問題）を踏まえると交流回路は来ないだろうと考えたため，今年は直流回路かコンデンサー回路，コイルを含んだ回路のどれかだろうなと思っていたからです。（現役生に配慮して共振回路は来ないと思っていたので，設問Ⅲは誤算でした）

⑴：穴埋めですね。簡単なのですが試験場で０と自信をもって答えるのは意外と怖いです。イの前のマイナスなども忘れそうで危なかったです😥

　ちなみに，ここでは導線aを外した直後の電荷分布なのか，その後十分に時間が経過したときの電荷分布を聞いているのかが不明瞭ですが，立式をしてやるとその２つの状態は等しいことがわかります（感覚的に両者の状態が等しいと考えるのはただの勘だと思います）。自分ははじめ，直後の電荷分布だと考えその旨を解答用紙に書きましたが，⑵を解く際にその但し書きが不要なことに気づきました。

⑵：電荷保存則と電圧の関係式を連立させて答えを求めに行きます。コンデンサー回路の定石なのですが計算が割と煩雑で，しかもここの答えがあとあと重要になりそうだったので，むちゃくちゃ計算に気を使いました。試験場では１番嫌なタイプな問題な気がしますね😥。符号にも気を付けながら，丁寧に答えをだします。（ここまでで15分）

　予想配点は，⑴が各１点で計２点，⑵は立式に２点，答えに各１点の計４点でしょうか。（計算が少し重たいので，式にも配点があると考えられます。）

設問Ⅲ：振動中心のずれた共振回路の問題ですね。最初，何が起こっているのかよくわからないです。事前にこのような問題に本格的に取り組んだことがあった人はとても少ないのでは？と後になって思いました。あまり差がつかなそうで難易度的にも[やや難]かなと思います。

⑴：合成容量Cを求めて，2π√LCを使うだけですね。これはシュンカンでした。こんなものは試験場では暗記して使えばいいですね。まずは，ウォーミングアップといった感じです😆

⑵：t＝0でのコイルの電圧は簡単にαV（ここではα＝2）だとシュンカンでわかりますね。問題は次で，I0の値を求めたいのですが，与えられた式がゴチャゴチャしていてよくわかりません。大抵そんなときは，微分積分を知らない受験生への配慮のために与えられた式だったりするので，ガン無視して微分してやったら答えが出ました。

　ちなみにですが，以下の式のようにエネルギー保存を使い，⑴の結果を使ってやることでも同じ結果を得ることができます（問題の流れ的には，この式は設問Ⅲ⑷の結果で分かることなので，これを書いて点数が来るのかは分かりませんね）。※以下の式のCは合成容量です。C0とは異なります。

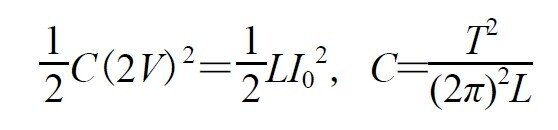
⑶：ウは穴埋めですね。穴埋めですが，よく見てみると穴埋めの意味がほとんどありません。出題者側の意図がよくわからないまま解答します。t＝T/4なので位相はπ/2です。コンデンサーにかかる電圧はcos関数なので，そのグラフをを考えてやって，その電圧がちょうど0のとき（流れる電流が最大のとき）を考えればいいですね。すると，設問Ⅱ⑵において，α＝0を代入したときのQ1，Q2の値を考えてやればいいとわかります。わざわざ式をたてるまでもありません。

　自分はここで，t＝T/4だから位相はπ/4！というヤバイ処理を頭の中でしてしまい，答えに√2がでてくる展開になってました。。。😭

　後半はQ3＝０となるときなので，設問Ⅱ⑵の答えから，α＝1になるような時間を求めればよいとわかります。元のαが2ですから，その1/2すなわち，位相がπ/3と5π/3のときで，その時刻はT/6と5T/6ですね。ここは正解できました（なぜなのか）。

　実は，僕はここまでα＝2を読み落としていて，この時刻を出す方法が全く分からず，３分くらい右往左往していました。結果的に問題文を読み直し，⑵の値もαを含まないものに変えて事なきを得ましたが，ここで結構な時間のロスをしてしまいました。問題文を最後までしっかり読むのは大切です😢。（ここまでで25分）

⑷：問題としては，E1，E2および，ΔEをただ計算するだけです（しかし，この計算がわりと面倒くさい！）。試験場ではでてきたΔEの値に対してあまり考察をすることはできないですが，この結果はとても面白いものですよね。

　自分は⑶の間違いが足を引っ張り，ここも落としてしまいました（計算式は書いてるので少しは点数来るかも？とは考えてますが…😥）

⑸：東大の十八番，グラフ選択問題です。こんなものは現象を理解できていればほとんどシュンカンで選べます。自分の選び方ですが，今回の場合，あるαと言われているので，グラフを完全に頭の中で確定させることができません。なので，消去法をとることにしました。まず，電圧がcos関数なので①，②，⑥はありえません。また，周期の関係で⑤もありえません，残るのは③と④です。ここで，任意のαに対して，Q3とQ4は位相がπ/2，すなわち時刻がT/4のときに等しくなる（⑶の考察）ので，③も消せますね。答えの④だけを書いて終了です。（ここまでで29分）

　予想配点は⑴２点，⑵電圧：１点，I0：２点，⑶ウ：１点，時刻：各１点，計３点⑷各１点，計３点，⑸２点。設問Ⅰ～Ⅲをあわせて合計26点。（TwitterのTLを見る限り，第２問を完答していらっしゃる方がほとんどいらっしゃらなそうなので，20点を上限としながらも，配点の合計は20を超えるのではないかと考えました。もし，合計20にするなら，⑶の時刻は合わせて1点，⑷はE1とE2を合わせて1点，また⑸も1点になると思います。他の設問１、２も訂正が必要ですが長くなるので省略。）

　計算量も多めで重厚な問題だなと思いました。一定以上の実力がつけば，そこからは，処理能力で差がつくことを痛感させられる問題かなと思います。ここ近年の東大電磁気の傾向として積極的に微積を使わせるきらいがありますが，今後も続いていくのでしょうか🤔

　前回よりも冗長になってしまいましたが（小ネタも挟めるところがなかった)，以上，ご覧いただきありがとうございました。明日は第３問「光ピンセット」について書きたいと思います。