構造用語「かけ算、わり算、分数」とは?1分でわかる意味を解説
構造力学では構造物にどのような「力」が働いているのか考えます。しかし「力」は見えません。私たちは見えない力を数式を使って考えます。主に微積分、三角関数は頻繁に使われますがもっと基本的なわり算やかけ算はどのような意味があるのか、おさらいをしておきましょう。
かけ算は「量を表す」
下の図の直方体の体積を求めてみましょう。

小学校の時に習いましたよね、そうです。たて×横×高さでしたね。
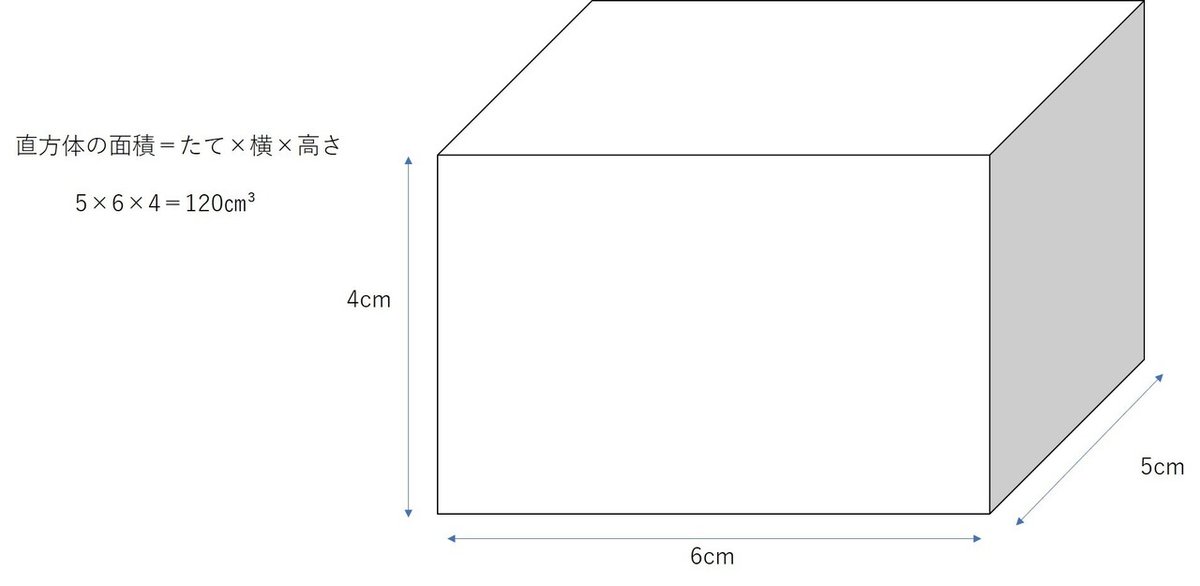
はい、このように出せました。ではどのようにしてこのような計算で体積が求められたのでしょうか。分かりやすいように1センチの立方体の集合体とみてみましょう。

まず、一番下の段に着目して面積をだします。5個×6個で立方体は30個あることがわかります。そして30個集まったものが4段あるので120個立方体があることがわかります。
1個のブロックが列を作り、幅を持つことで面積を持つようになり、高さ方向に積み上げると体積を持つようになります。かけ算、積というのは集合体をもつということをイメージできるようになりましょう。また、方向をもつという性質があることも押さえておきましょう。
続いてはわり算です。まず基本をおさらいしましょう。

わり算には二つの意味があります。それは「等分する」という考えです。
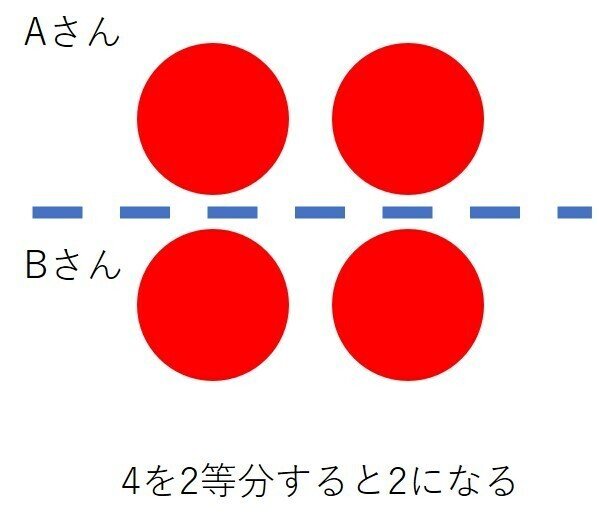
もう一つは「中にいくつはいっているかという」考え方です。

上の絵の場合「81の中に9はどれくらいはいっているか」の式になります。人口密度を出すときもこのように出します。構造力学ではこの考え方がよくでてきます。それではわり算を使った考え方をもう少し見ていきましょう。
わり算の考え方①「平均」
平均とはいくつかの数を等しい大きさに均したものです。例えば

上の図は6か所に積まれた積み木があります。全部でいくつでしょう。
答えは24個です。数えるのが大変だったと思います。それではこの積み木は均していきましょう。

こうすると数えやすくなりました。つまり平均は4個になります。すべての積み木の合計を位置の数で割ると平均が求められます。

このように式を3つ書かれるとわかりにくいですよね。それでは図で表します。

このように図にするとわかりやすいです。
わり算の考え方②「単位量」
単位量とはよく車の燃費で使用されたりします。例えば1リットル当たりどれくらい走れるのかなど、1つあたりの量をはかるときに使われます。例えばこちらの下図をみてください。

この1m2当たりどれくらい人数がいるかというものが単位量です。次に下の問題をみてください。

この場合、二つの考え方があります。まず一つめは下図です。

こちらの考え方とはほかに「1人あたりの面積」で比べることもできます。面積÷人数で1人あたりどのくらいの面積をもっているのかがわかります。

この上図のような求め方は人口密度などで用いられます。
かけ算わり算は非常に大切な考え方なのでしっかり押さえましょう。
