【Read between lines】Peskin, Schroeder "An Introduction to Quantum Field Theory" p. 368 (An example of exact convex form of the effective potential)

Key words

• Effective potential

• Macroscopic region

• Magnetic domain

Relevant section

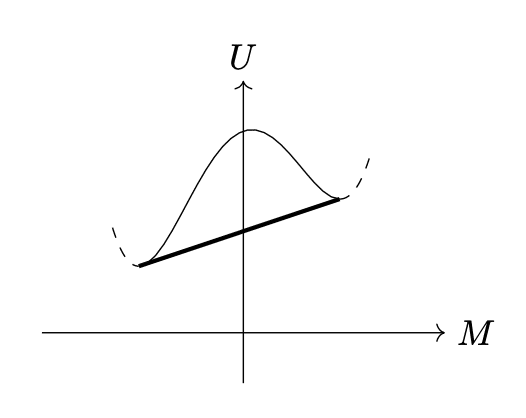
The assumption of a constant background field gives a large value of the effective potential, as indicated the figure. We can obtain a lower-energy configuration by considering states with macroscopic regions in which $${\braket{\phi}=\phi_1}$$ and other regions in which $${\braket{\phi}=\phi_3}$$, in such a way that the average value of $${\braket{\phi}}$$ over the whole system is $${\phi_\mathrm{cl}}$$. For such a configuration, the average vacuum energy is given by 

$$
V_\mathrm{eff}(\phi_\mathrm{cl})=xV_\mathrm{eff}(\phi_1)+(1-x)V_\mathrm{eff}(\phi_3)
$$

Solution

Let us see an example for this type of potential (not a quantum field but magnetic domain). 

Settings

Prepare a strong magnet and a weak magnet, and adhere their S-poles together in a way that they face opposite directions. The adhesive should possess sufficient strength to prevent their separation.

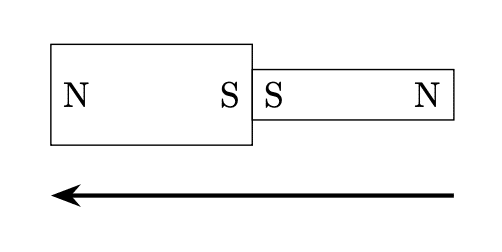
Prepare a total of N such magnets and arrange them in a linear configuration as illustrated in the figure below. In the depicted figure, the positive z-direction corresponds to the upward direction, and the z-component of magnetization for the N magnets is denoted as M. The magnets are restricted to rotation only within the plane of the paper.

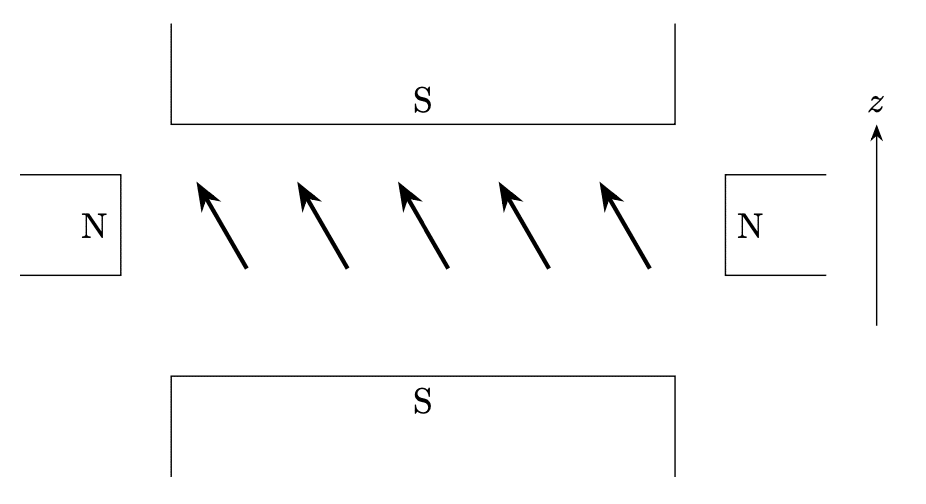
In addition to this, larger magnets are positioned as indicated in the figure above. The configuration that imparts the highest stability involves aligning all magnets in the +z direction using this external magnetic field.

Potential and magnetization

In the event that all the magnets are simultaneously rotated, and subsequently M and the potential U are charted on a graph, the expected outcome is represented in the following figure. The metastable state corresponds to all magnets being oriented downward.

Only the thick line is realized, since M has max and min.

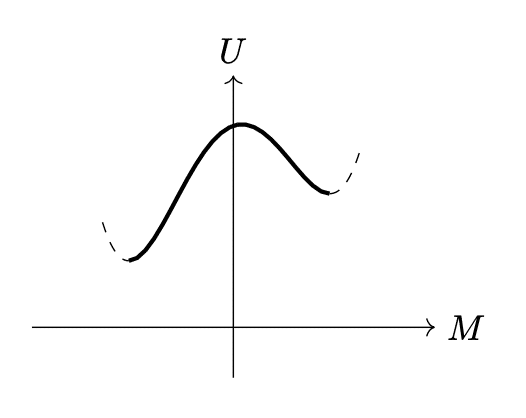
When the individual magnets are permitted to rotate independently, the transition from the most stable state to the metastable state can be achieved with lower energy consumption by sequentially reversing the orientations of the magnets, rather than rotating them all simultaneously. In cases where N is adequately large, the interaction between magnets exhibiting different orientations can be disregarded, enabling the potential to be simplified into a basic combination of the most stable and metastable states — essentially, a first-order approximation in terms of x.

These two parts are magnetic domains.

Given that the total magnetization M is also expressed within the first order of x, the potential transitions across the line segment connecting the most stable and metastable configurations.