【Read between lines】Peskin, Schroeder "An Introduction to Quantum Field Theory" p. 301 (derivative of determinant in Penrose graphical notation for Gaussian integral of Grassmann numbers)

Key Words

• Grassmann number

• Gaussian integral

• Determinant

• Levi-Civita symbol

• Penrose graphical notation

Relevant section

Similarly, you can show that

$$
\left(\prod_i\int d\theta_i^\ast d\theta_i\right)\theta_k\theta_l^\ast e^{-\theta_i^\ast B_{ij}\theta_j}=(\det B)(B^{-1})_{kl}.
$$

Inserting another pair $${\theta_m\theta_n^\ast}$$ in the integrand would yield a second factor $${(B^{-1})_{mn}}$$, and a second term in which the indices $${l}$$ and $${n}$$ are interchanged (the sum of all possible pairings).

Solution

First, in this article you need knowledge about Penrose graphical notation. 

We can show the relations via derivatives:

$$
\left(\prod_i\int d\theta_i^\ast d\theta_i\right)\theta_k\theta_l^\ast e^{-\theta_i^\ast B_{ij}\theta_j}=\frac{∂}{∂B_{kl}}\left(\prod_i\int d\theta_i^\ast d\theta_i\right)e^{-\theta_i^\ast B_{ij}\theta_j}=\frac{∂}{∂B_{kl}}(\det B).
$$

Determinant is represented as

$$
\det B=\frac{1}{n!}\epsilon_{1\cdots n}^{i_1\cdots i_n}\epsilon_{j_1\cdots j_n}^{1\cdots n}B_{i_1}^{j_1}\cdots B_{i_n}^{j_n}.
$$

This is shown in the following notation:

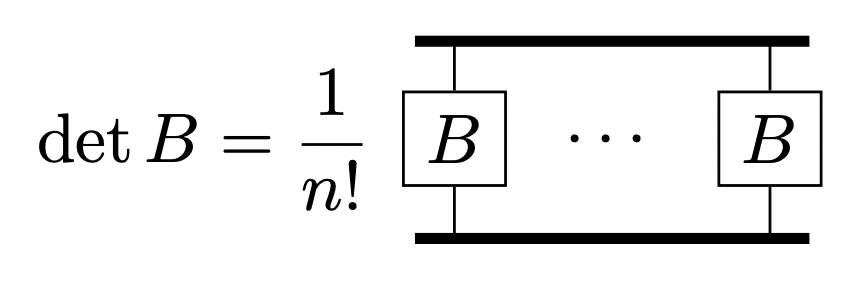
The derivative by $${B_{kl}}$$ is,

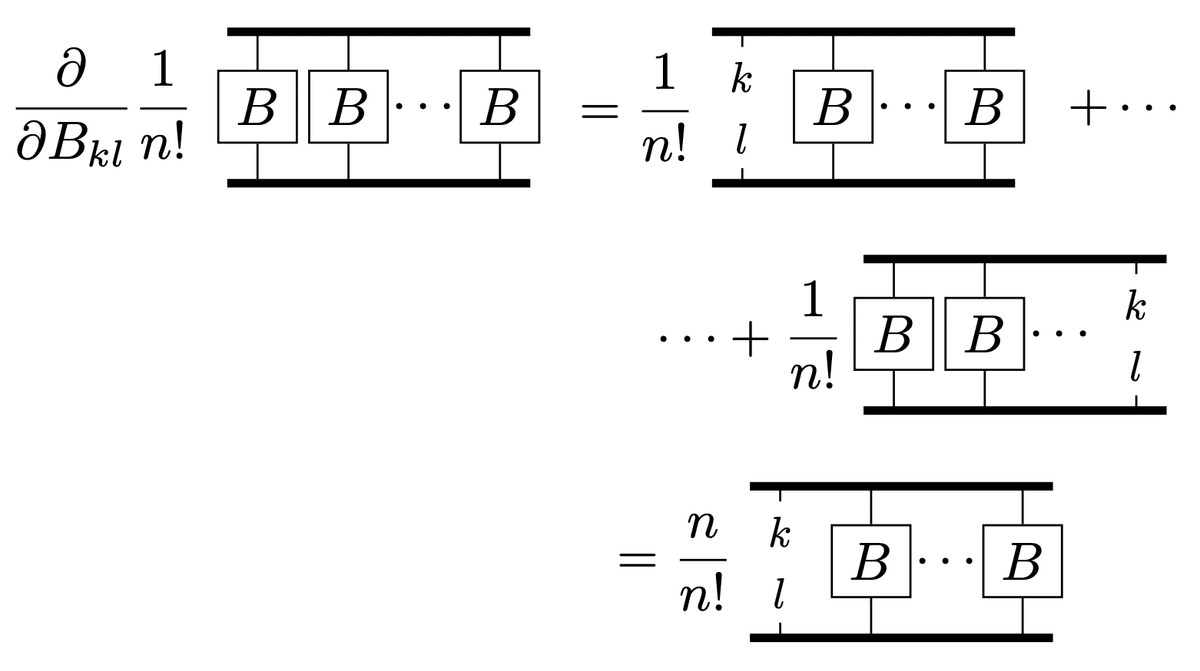
On the other hand, $${B^{-1}}$$ is

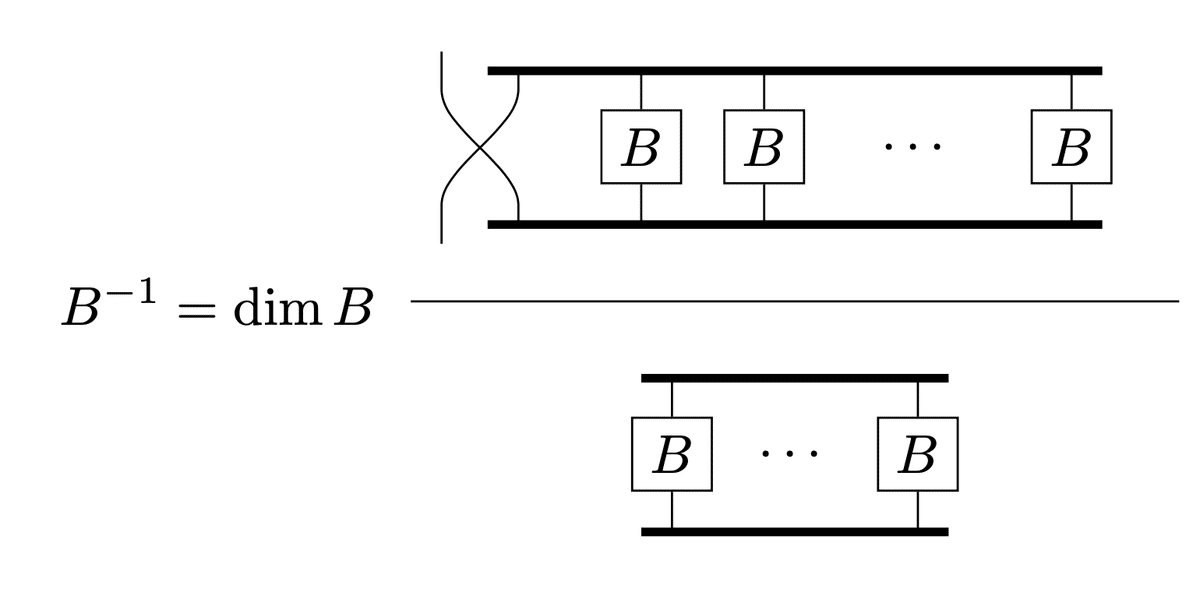
so $${∂\det B/∂B_{kl}=(B^{-1}\det B)_{kl}}$$.