【Read between lines】Peskin, Schroeder "An Introduction to Quantum Field Theory" p. 39 (The commutation relations of the generators of Lorentz group with Penrose's graphical notation)

Key words

• commutation

• Lorentz transformation

• generator

• Penrose's graphical notation

About Penrose's graphical notation, see How to use Penrose graphical notation for Levi-Civita symbol with some formulae. 

Relevant section

To determine the commutation rules of the Lorentz algebra, we can now simply compute the commutators of the differential operators (3.16). The result is

$$
[J^{\mu\nu},J^{\rho\sigma}]=i(g^{\nu\rho}J^{\mu\sigma}-g^{\mu\rho}J^{\nu\sigma}-g^{\nu\sigma}J^{\mu\rho}+g^{\mu\sigma}J^{\nu\rho}). \qquad(3.17)
$$

Solution

First, $${J^{\mu\nu}}$$ is represented in Penrose's graphical notation as the figure. 

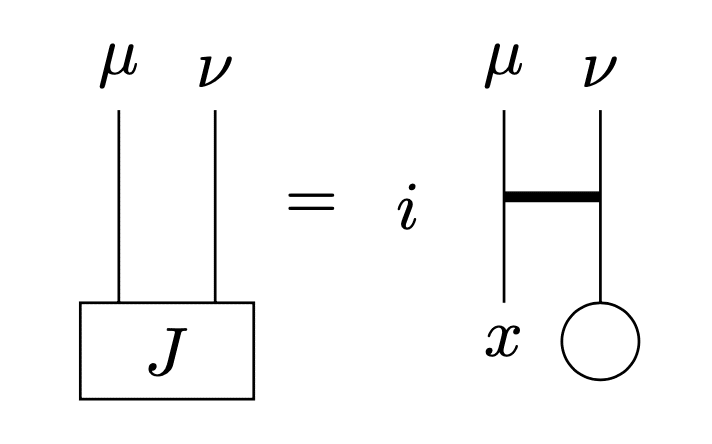
Note that derivative operators differentiate all the subsequents. We can compute the commutator by Leibniz rule. Indices are omitted. 

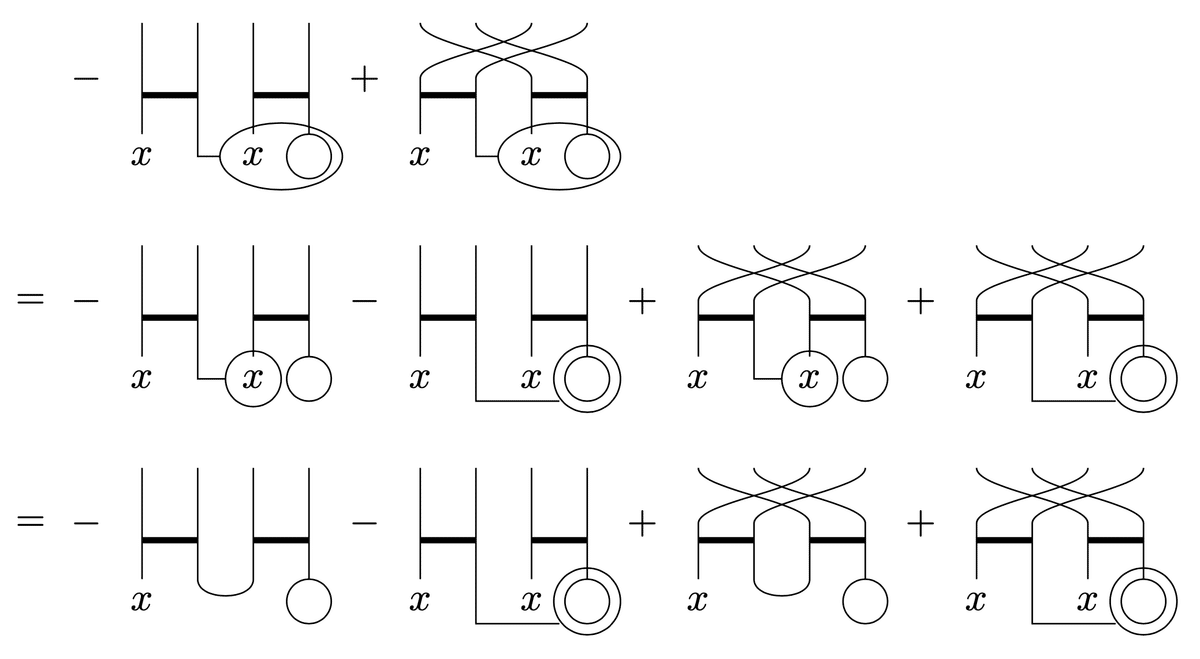
Here we used $${\partial^\alpha x^\beta=g^{\alpha\gamma}\partial_\gamma x^\beta=g^{\alpha\gamma}\delta_\gamma^\beta=g^{\alpha\beta}}$$ for the first and the third terms. The second and forth terms are identical. For the third term, 

We get, therefore, the commutation relation. 

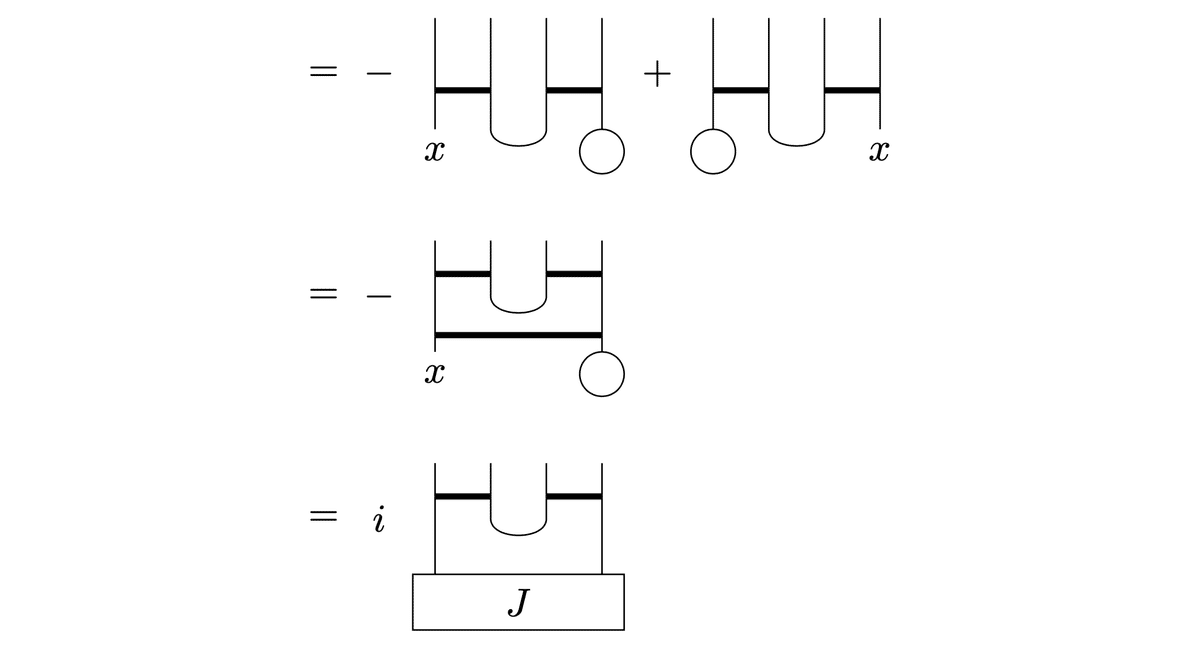
The last representation is $${ig^{\nu\rho}J^{\mu\sigma}-ig^{\mu\rho}J^{\nu\sigma}-ig^{\nu\sigma}J^{\mu\rho}+ig^{\mu\sigma}J^{\nu\rho}}$$, the same as written on the textbook.