【Read between lines】Peskin, Shcroeder "An Introduction to Quantum Field Theory" pp. 28-29 (Continuous Lorentz transformation for spacelike x-y to y-x)

Key words

• Lorentz transformation

• spacelike

• light cone

Relevant section

When $${(x-y)^2<0}$$, we can perform a Lorentz transformation on the second term (since each term is it separately Lorentz invariant), taking $${(x -y)\to-(x-y)}$$, as shown in Fig. 2.4. The two terms are therefore equal and cancel to give zero; causality is preserved. Note that if $${(x-y)^2>0}$$ there is no continuous Lorentz transformation that takes $${(x-y)\to-(x-y)}$$.

Solution

Fig. 2.4 on the textbook shows the light cone and hyperboloid. Since Lorentz transformation is continuous, there have to be a continuous path connecting two points on the hyperboloid, if you get one point by transformation from the other.

Time goes upward. x'-y' and -(x'-y') are spacelike, x-y and -(x-y) are timelike.

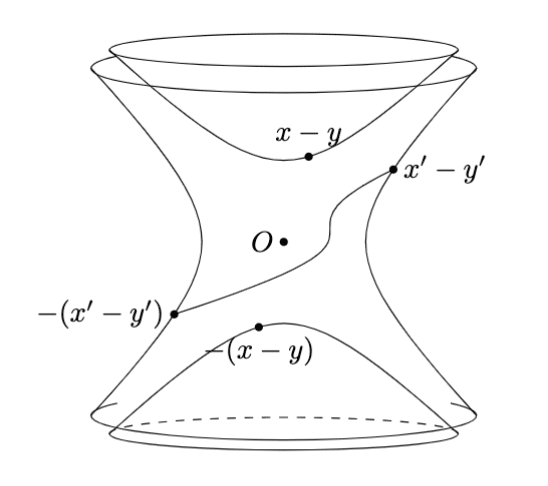
As the figure shows, a hyperboloid out of the light cone is connected, otherwise one in the cone is separated into two parts. Therefore there is no connected path between timelike symmetric points, i.e., no continuous transformation between $${(x-y)\to-(x-y)}$$.

Why hyperboloid

Let us consider the shape of the surface on which a transformed point moves. We cannot draw 4-dim space, so we use $${z=0}$$ subspace. When we transform $${x^\mu=(x^0, x^1, x^2, x^3)\mapsto x'=(\gamma x^0-\gamma\beta x^1, \gamma x^1-\gamma\beta x^0, x^2, x^3)}$$, this transformation is represented as the following eqs.

$$
\begin{array}{ll}x'^0=x^0\cosh\theta-x^1\sinh\theta\\x'^1=x^1\cosh\theta-x^0\sinh\theta\\\beta=\tanh\theta\end{array}
$$

We get, 

$$
\begin{array}{rcl}(x^{02}-x^{12})\cosh\theta&=&x^0x'^0-x^1x'^1\\(x^{02}-x^{12})\sinh\theta&=&x^0x'^1-x^1x'^0\\\therefore\quad(x^{02}-x^{12})^2&=&(x^0x'^0-x^1x'^1)^2-(x^0x'^1-x^1x'^0)^2\\&=&(x^{02}-x^{12})(x'^{02}-x'^{12}).\end{array}
$$

This $${x'}$$ represents a hyperbola that passes $${x}$$. If we perform Lorentz transformation only in space, the transformation is only continuous rotation of space; the surface on which Lorentz transformed point moves is a hyperboloid.