
キッテル固体物理学入門 演習問題解答 第1章
誤り・質問等ありましたら、遠慮なくご連絡願います。
1. 正4面体構造の角
体対角線のベクトルは
$$
\bm{a}_1=\left(\begin{matrix}1\\-1\\-1\end{matrix}\right),\;\bm{a}_2=\left(\begin{matrix}1\\1\\1\end{matrix}\right),\;\bm{a}_3=\left(\begin{matrix}-1\\-1\\1\end{matrix}\right)
$$
と表せるので、余弦定理を使えば、
$$
\cos\gamma=\dfrac{|\bm{a}_1|^2+|\bm{a}_2|^2}{2\bm{a}_1\cdot\bm{a}_2}=-\dfrac{1}{3}
$$
計算機によると$${\gamma=1.91…\:\mathrm{rad}\approx109º}$$である。
2. 面指数
通常の軸が下図で黒のようになるのに対し、基本結晶軸は赤で配される。
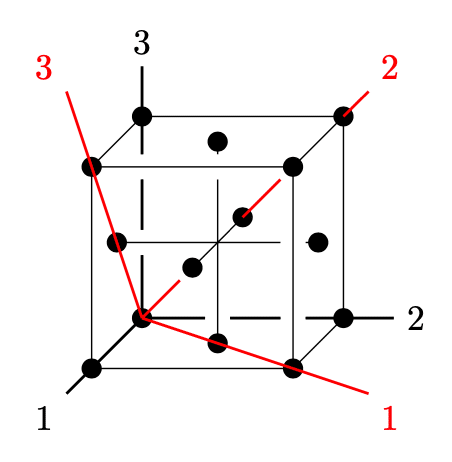
通常の指数で(100)だったものは(101)に平行となる。
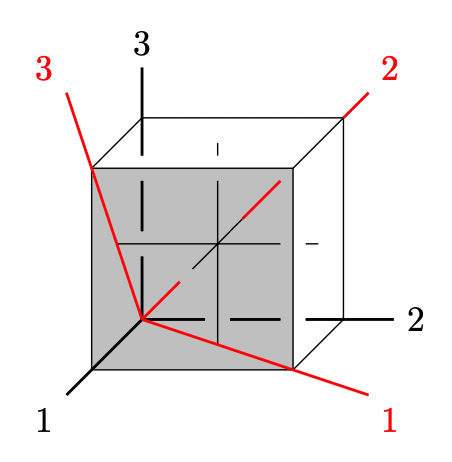
(001)だったものは(011)に平行となる。

面が軸を切る位置を明示的に表すのであれば、基本結晶軸での表現はそれぞれ(1/2 0 1/2), (0 1/2 1/2)と表される。
3. hcp構造
最密充填のとき$${c}$$は1辺$${a}$$の正4面体の高さの2倍に相当する。

図の赤い二等辺三角形について、図から高さを求めると$${c/2=\sqrt{6}a/3}$$となるので、
$$
\dfrac{c}{a}=\dfrac{2\sqrt{2}}{\sqrt3}=\left(\dfrac{8}{3}\right)^{1/2}.
$$
