太さが変わると強度も変わる?~飛行機の翼と傘の骨で「片持ち梁」を学ぶ~(R6年度技術士一次試験基礎科目過去問より)
1. はじめに:日常に潜む「片持ちばり」って何?
家の周りや街を歩くと、「ものが片側だけで支えられている」構造によく気づくことがあります。たとえば、家の縁側やバルコニー、道路標識や看板の支柱など。実は、空を飛ぶ飛行機の翼や、雨の日の傘の骨も同じく、一端だけで支えられている部分があるのです。
こうした形を片持ち梁といい、材料力学・構造力学の基礎モデルの一つです。そして、そこに荷重が均等に広がって載る場合は、「等分布荷重を受ける片持ち梁」という形になります。
本記事では、この「片持ち梁+等分布荷重」を、飛行機の翼と傘の骨という2つの例で見ていきましょう。エンジニアがどんな計算をし、どんな点を考慮して設計しているか、少しでもイメージをつかんでいただければと思います。

2. 飛行機の翼:空に突き出す片持ち梁
2.1 胴体に根元を固定、先端は自由端
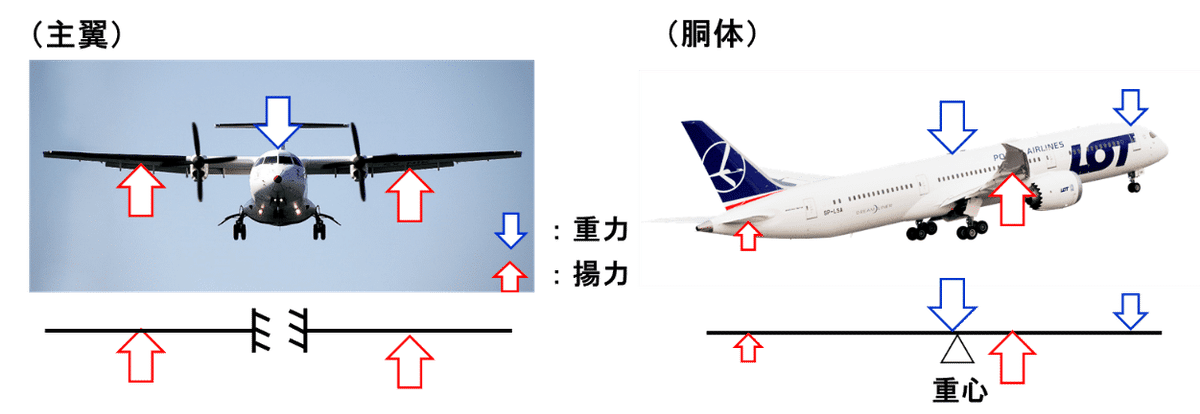
飛行機を横から見ると、左右に大きく広がる翼が胴体部分だけで支えられていることに気づきます。先端側に支えがないため、まさに一端固定・他端自由の片持ちばりになっています。
さらに、翼全体には飛行中の揚力が広く作用します。厳密に言えば分布にむらがありますが、まずは等分布荷重として近似する形で、片持ち梁の基本計算を行うことが多いです。
2.2 エンジニアは何を考えているのか?
軽量化と強度の両立
翼が重すぎると燃費が悪化し、軽すぎると折れるリスクが高い。エンジニアは断面二次モーメントを大きく確保する形状を用いたり、高強度・軽量素材(アルミやCFRP等)を使ったりして、ちょうどよいバランスを探ります。たわみと飛行特性
翼がある程度しなるのは想定内ですが、しなりすぎるとフラッター(振動破壊)を起こす危険があります。
$${M_{max}}$$(後述の最大曲げモーメント)や$${\delta_{max}}$$(最大たわみ)を計算し、過度なしなりを防ぐように設計します。疲労破壊とメンテナンス
飛行機は離着陸や乱気流で大きな力を何度も受けるため、翼根元が繰り返し応力で疲労破壊しやすい。定期的な点検・補修が不可欠です。
3. 傘の骨:身近な「等分布荷重」を想定できるモデル
3.1 どうして傘の骨が片持ち梁状態に?
雨の日に使う傘を開くと、中心の軸から放射状に伸びる骨があり、根元は軸に固定、先端は布を支える形です。これは図式的に見れば片持ち梁に近い構造。
傘布の張力や雨粒の重さ、風による力などが骨全体に分散してかかるとみなせば、等分布荷重に似たモデルで強度の概略を把握できます。実際には負荷のかかり方に偏りがあるものの、エンジニアはまずシンプルなモデルから設計を始めるわけです。
3.2 エンジニアの視点
折りたたみと強度の両立
傘の骨はできるだけ細く、軽くしたいが、強風で簡単に折れない太さも必要。数式で骨径を見積り、最低限の強度を確保します。コストと寿命
安価な傘は骨が極端に細く、少し風が吹くと折れがち。高級傘は骨を太めにし、強度素材を使うことで壊れにくくします。
エンジニアは「使い捨て前提か、長期使用前提か」を踏まえ、最適な骨径を選定します。軽量性・収納性
飛行機のように繰り返し荷重の疲労破壊まで厳密には計算しないにしても、「ある程度曲がらない太さ」と「折り畳みやすさ」の兼ね合いを図ります。
4. 材料力学の基礎:片持ち梁 + 等分布荷重をどう計算?
片持ち梁に等分布荷重 $${w}$$(単位: [N/m]) が掛かるとき、まず注目するのは最大曲げモーメント $${M_{max}}$$ です。
$${M_{max} = \frac{ w \times L^2}{2 }}$$
ここで $${L}$$ は梁の長さ。飛行機の翼なら胴体付近、傘の骨なら中心軸付近が、この最大モーメントを受ける“危険断面”となるわけです。
さらに、曲げ応力 $${\sigma_{max}}$$ は
$${\sigma_{max} = \frac{ M_{max} \times c }{ I }}$$
で求められます。
$${c}$$ : 断面の中心から外縁までの距離(円なら $${D / 2}$$)
$${I}$$ : 断面二次モーメント(太さや形状に依存)
一方、梁のたわみ $${\delta_{max}}$$ は
$${\delta_{max} \propto \frac{1}{E \times I}}$$
という形なので、断面が太いほど ( $${I}$$ が大きいほど ) 変形が小さくなります。
5. 太さの4乗で効く断面二次モーメントの威力
円形断面で直径 $${D}$$ の場合、断面二次モーメント $${I}$$ は
$${I = \frac{\pi , D^4}{64}.}$$
ここで $${D}$$ を2倍にすると $${D^4}$$ は16倍になり、曲げ応力やたわみを一気に減らせます。
飛行機の翼: 少し桁を太くするだけで破断リスクが大幅減
傘の骨: わずかに太くするだけで風に負けにくくなる
ただし、太くすれば重さやコストも増すため、エンジニアは計算と試作を重ねて最適を探ります。
6. 日常でどう活きる? エンジニアの思考
飛行機の翼
燃費(重量)と強度(安全性)をにらむ
振動・フラッター対策で詳細な解析
長期運用での金属疲労を定期点検で防止
傘の骨
軽量で折り畳みやすいが、そこそこの風には耐えられるように骨径を決める
コストと耐久性のトレードオフ
実際には壊れたら買い換えでもいいが、高級モデルは長く使う設計も
「片持ち梁+等分布荷重」は、看板の支柱や街灯柱など、身近な所でも応用されている理屈。材料力学の数式をちょっと知ると、「なぜ太さが少し違うだけであんなに強度や変形が変わるの?」が腑に落ちるようになります。
7. まとめ
飛行機の翼: 胴体で翼を支える片持ち梁に、揚力(等分布荷重)がかかる → 軽量化と強度確保の絶妙バランス
傘の骨: 中心軸にのみ固定された骨に、布・雨・風が分散 → 細く折りたたみできるが、ある程度太くしないとすぐ折れる
太さの4乗効果: 断面二次モーメント($${I \propto D^4}$$など)で曲げ応力・たわみが大きく変化
「太さ2倍で強度8倍・変形1/16」などの話は、飛行機でも傘でも実感できるポイント
街や日常を見渡すと、意外に片持ち梁の構造物が多いものです。飛行機の翼が上下に揺れても「計算内なのかな」と安心できるし、傘の骨が弱いのも「$${I \propto D^4}$$ が足りないからか…」と納得できるかもしれません。
難しそうな材料力学ですが、こうした例を知るだけでも、数式の裏にある“ものづくりの知恵”がちょっと身近に感じられるようになるはずです。
8. おまけ:最初に提供した過去問と解法解説
最後に、本記事のテーマと関連する**過去問**を以下に紹介します。
【問題文】
I-1-3 次の記述の、___ に入る語句の組み合わせとして、最も適切なものはどれか。
断面が円形の等分布荷重を受ける片持ちばりにおいて、 最大曲げ応力は断面の円の直径のアにイし、最大たわみは断面の円の直径のウにエする。
選択肢としては、
1) ア=3乗, イ=反比例, ウ=4乗, エ=反比例
2) ア=4乗, イ=比例, ウ=4乗, エ=反比例
3) ア=4乗, イ=反比例, ウ=3乗, エ=比例
4) ア=4乗, イ=反比例, ウ=3乗, エ=反比例
5) ア=3乗, イ=反比例, ウ=4乗, エ=比例
【解説と正解】
材料力学の公式から、 最大曲げ応力 $${\sigma_{max} \propto 1 / D^3}$$
最大たわみ$${\delta_{max} \propto 1 / D^4}$$ となるため
- ア=3乗
- イ=反比例
- ウ=4乗
- エ=反比例
が正解となります。すなわち選択肢(1)が正解です。 直径$${D}$$を2倍にすると、曲げ応力は1/8、たわみは1/16になる――“4乗効果”がここでも問われているわけです。
このように、飛行機の翼と傘の骨の例から、「片持ち梁+等分布荷重」の考え方、そして関連する過去問の解法までを見てきました。
材料力学は数式ばかりで難しく感じますが、実はこうした身近な道具や大きな乗り物にも直結しています。
街や日常を見ながら「ここは片持ちばりになっているのかな?」と想像してみると、ちょっと工学が身近に感じられるかもしれません。
