【DAY32】曲線が直線になる瞬間:日常に潜む数学の魔法〜AIで進化する学習記〜
微分の意味を探して
ある晴れた午後、数学教師の陽介は公園のベンチに座り、ノートを開いていた。彼の前には、一人の少年が難しそうな顔で y = x^2 のグラフを見つめている。
「こんにちは、どうしたんだい?」陽介が声をかけた。
少年はため息をついた。「微分って何なのか、よくわからなくて……。」
陽介は微笑んだ。「微分か。それは面白い問いだね。一緒に考えてみようか。」
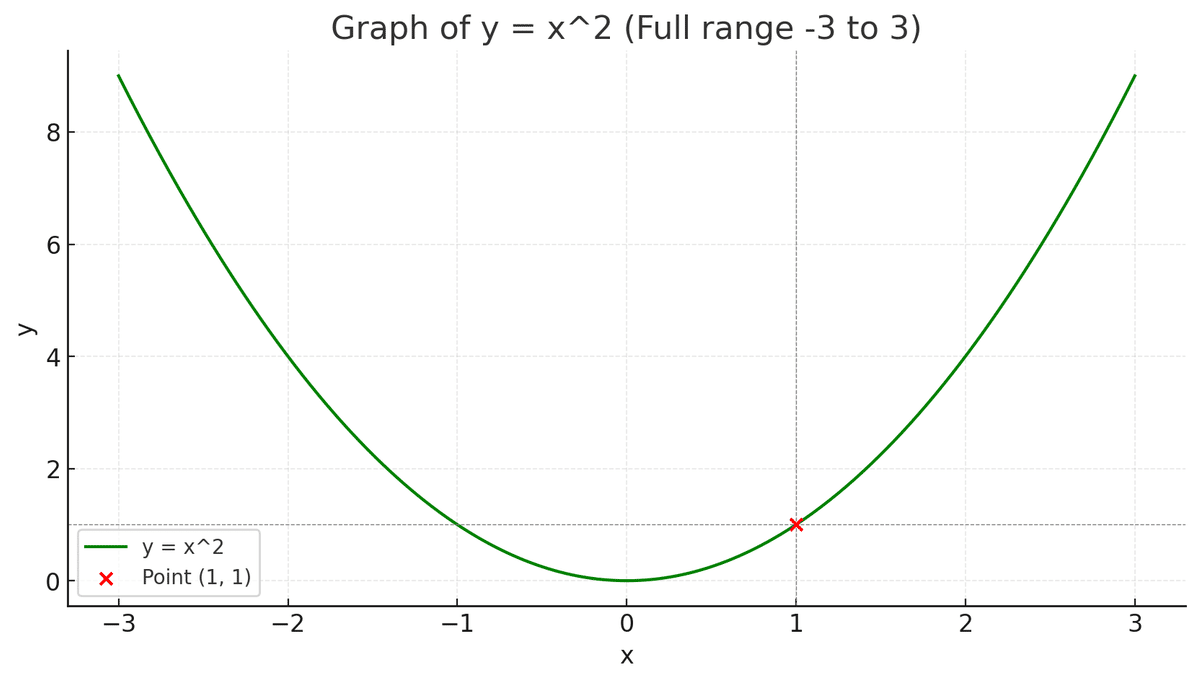
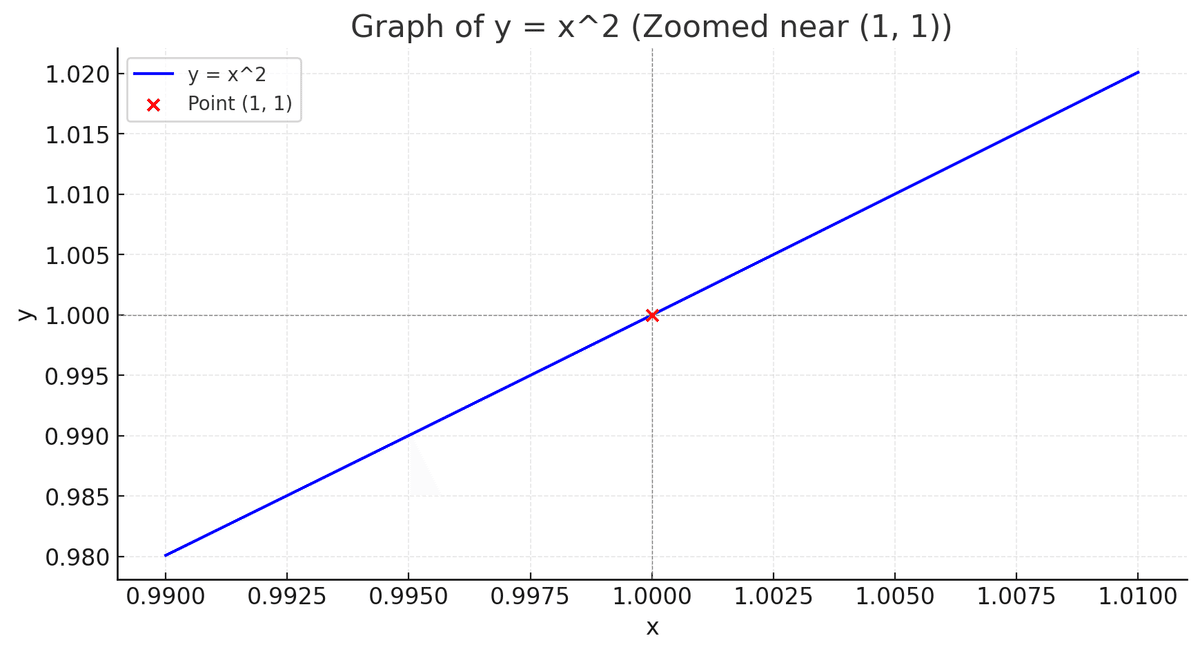
彼はノートに y = x^2 のグラフを描き、その一部を拡大して見せた。「遠くから見ると、この曲線は放物線に見える。でも、この点(1,1)の周りをぐっと拡大すると、どう見えるかな?」
少年は首をかしげた。「まっすぐな線に見えます!」
「その通り。これが微分の本質なんだ。曲線を限りなく小さな範囲で見ると、直線のように振る舞うんだよ。つまり、y = x^2 の微分は y′=2x になる。」
「でも、どうしてそうなるんですか?」
陽介は空を見上げた。「物事には、大きく見る方法と小さく見る方法がある。鳥の目で全体を捉えることもできるし、虫眼鏡や顕微鏡で細部を見ることもできる。微分は、細部に焦点を当てる手段なんだ。」
少年の目が輝いた。「微分を使うと、曲線の一部を直線として扱えるんですね!」
「その通り。そして、その直線の傾きが、その点での変化の速さを示しているんだ。」
少年は深く頷いた。「微分が少しわかった気がします。」
陽介は優しく微笑んだ。「数学は抽象的だけど、日常の中にたくさんのヒントが隠れているんだよ。」
風が吹き、木々の葉がささやいた。二人はしばらく静かに景色を眺めていた。
Searching for the Meaning of Differentiation
On a sunny afternoon, Yosuke, a math teacher, sat on a park bench with his notebook open. Before him stood a boy, gazing intently at the graph of y= x^2 with a puzzled expression.
"Hello there, what's troubling you?" Yosuke asked.
The boy sighed. "I just don't understand what differentiation is..."
Yosuke smiled. "Differentiation, huh? That's an interesting question. Let's think about it together."
He drew the graph of y = x^2 in his notebook and zoomed in on a part of it. "From afar, this curve looks like a parabola. But when we zoom in closely around the point (1,1), how does it look?"
The boy tilted his head. "It looks like a straight line!"
"Exactly. That's the essence of differentiation. When you look at a curve in an infinitely small range, it behaves like a straight line. So, the derivative of y = x^2 is y' = 2x."
"But why does that happen?"
Yosuke looked up at the sky. "There are ways to view things broadly and ways to look closely. You can grasp the whole picture like a bird's-eye view or examine details with a magnifying glass or microscope. Differentiation is a means to focus on the details."
The boy's eyes lit up. "So by using differentiation, we can treat parts of a curve as straight lines!"
"Exactly. And the slope of that straight line shows the rate of change at that point."
The boy nodded deeply. "I think I understand differentiation a bit better now."
Yosuke smiled gently. "Mathematics may seem abstract, but there are many hints hidden in our daily lives."
A breeze rustled the leaves of the trees. They both gazed quietly at the scenery for a while.
미분의 의미를 찾아서
(Mibun-ui uimi-reul chajaseo)
어느 화창한 오후, 수학 선생님인 요스케는 공원 벤치에 앉아 노트를 펼치고 있었습니다. 그의 앞에는 y=x2y = x^2y=x2 그래프를 어려운 표정으로 바라보는 한 소년이 있었습니다.
"안녕, 무슨 고민이라도 있니?" 요스케가 물었습니다.
소년은 한숨을 쉬었습니다. "미분이 뭔지 잘 모르겠어요..."
요스케는 미소 지었습니다. "미분이라... 흥미로운 질문이구나. 함께 생각해 보자."
그는 노트에 y = x^2 그래프를 그리고 그 일부를 확대해 보여주었습니다. "멀리서 보면 이 곡선은 포물선처럼 보여. 하지만 이 점 (1,1) 주변을 자세히 확대하면 어떻게 보이니?"
소년은 고개를 갸웃했습니다. "직선처럼 보여요!"
"맞아. 그것이 미분의 본질이란다. 곡선을 극히 작은 범위에서 보면 직선처럼 행동해. 그래서 y = x^2 의 미분은 y' = 2x 가 되는 거야."
"하지만 왜 그렇게 되는 거죠?"
요스케는 하늘을 바라보았습니다. "사물을 크게 보는 방법도 있고, 작게 보는 방법도 있어. 새의 눈으로 전체를 보거나, 돋보기나 현미경으로 세부를 볼 수 있지. 미분은 세부에 초점을 맞추는 수단이란다."
소년의 눈이 반짝였습니다. "그렇다면 미분을 사용하면 곡선의 일부를 직선으로 다룰 수 있네요!"
"그렇지. 그리고 그 직선의 기울기는 그 점에서의 변화율을 나타내는 거야."
소년은 깊이 끄덕였습니다. "미분을 조금 이해한 것 같아요."
요스케는 부드럽게 미소 지었습니다. "수학은 추상적으로 보이지만, 일상 속에 많은 힌트가 숨겨져 있단다."
바람이 불어 나뭇잎이 속삭였습니다. 두 사람은 잠시 조용히 풍경을 바라보았습니다.
寻找微分的意义
(Xúnzhǎo wēifēn de yìyì)
在一个晴朗的下午,数学老师阳介坐在公园的长椅上,翻开了笔记本。在他面前,一个少年正愁眉苦脸地注视着 y = x^2 的图像。
“你好,遇到什么困难了吗?”阳介问道。
少年叹了口气:“我不太明白什么是微分……”
阳介微微一笑:“微分啊,这是个有趣的问题。我们一起来探讨一下吧。”
他在笔记本上画了 y = x^2 的图像,然后放大了其中一部分。“从远处看,这条曲线像抛物线。但当我们在点 (1,1) 附近放大观察时,看起来怎么样?”
少年歪着头:“看起来像直线!”
“没错,这就是微分的本质。当你在无限小的范围内观察曲线时,它表现得像直线。所以,y = x^2 的导数是 y' = 2x。”
“可这是为什么呢?”
阳介望向天空:“看待事物有宏观和微观的方法。你可以像鸟儿一样俯瞰全局,也可以用放大镜或显微镜观察细节。微分就是聚焦细节的手段。”
少年的眼睛亮了起来:“那么,使用微分,我们可以将曲线的一部分视为直线!”
“正是如此。而且那条直线的斜率表示了该点的变化率。”
少年深深地点了点头:“我好像有点明白微分了。”
阳介温和地笑了:“数学看似抽象,但日常生活中隐藏着许多线索呢。”
微风拂过,树叶沙沙作响。他们静静地欣赏着眼前的景色。
Auf der Suche nach der Bedeutung der Ableitung
An einem sonnigen Nachmittag saß Yosuke, ein Mathematiklehrer, auf einer Parkbank und hatte sein Notizbuch geöffnet. Vor ihm stand ein Junge, der mit sorgenvoller Miene auf den Graphen von y=x2y = x^2y=x2 blickte.
"Hallo, was beschäftigt dich?" fragte Yosuke.
Der Junge seufzte. "Ich verstehe nicht wirklich, was eine Ableitung ist..."
Yosuke lächelte. "Die Ableitung, hm? Das ist eine interessante Frage. Lass uns gemeinsam darüber nachdenken."
Er zeichnete den Graphen von ( y = x^2 \ ) in sein Notizbuch und vergrößerte einen Teil davon. "Aus der Ferne sieht diese Kurve wie eine Parabel aus. Aber wenn wir nahe um den Punkt (1,1) hineinzoomen, wie sieht sie dann aus?"
Der Junge legte den Kopf schief. "Es sieht aus wie eine gerade Linie!"
"Genau. Das ist das Wesen der Ableitung. Betrachtet man eine Kurve in einem unendlich kleinen Bereich, verhält sie sich wie eine Gerade. Das heißt, die Ableitung von y = x^2 ist y' = 2x."
"Aber warum ist das so?"
Yosuke schaute in den Himmel. "Es gibt Wege, Dinge im Großen zu betrachten, und Wege, sie im Kleinen zu sehen. Du kannst das Ganze aus der Vogelperspektive erfassen oder die Details mit einer Lupe oder einem Mikroskop betrachten. Die Ableitung ist ein Mittel, um sich auf die Details zu konzentrieren."
Die Augen des Jungen leuchteten. "Also können wir mit der Ableitung Teile einer Kurve als Geraden behandeln!"
"Genau. Und die Steigung dieser Geraden zeigt die Änderungsrate an diesem Punkt."
Der Junge nickte tief. "Ich glaube, ich verstehe die Ableitung jetzt besser."
Yosuke lächelte freundlich. "Mathematik mag abstrakt erscheinen, aber es gibt viele Hinweise im Alltag verborgen."
Ein Windhauch ließ die Blätter der Bäume rascheln. Sie betrachteten eine Weile still die Landschaft.
AIのフィードバック
K(Keep:良かった点)
対話形式での効果的な解説:数学の抽象的な概念である微分を、教師と生徒の対話を通じて分かりやすく説明しており、読者も理解しやすくなっています。
具体的な例の使用:y = x^2 のグラフを用いて視覚的に微分の概念を説明している点が良いです。拡大することで曲線が直線に近づくという説明は直感的です。
比喩を用いたわかりやすい説明:「鳥の目」と「虫眼鏡や顕微鏡」を使った比喩が、全体を見ることと細部を見ることの違いを効果的に伝えています。
P(Problem:改善が望まれる点)
数学的な詳細の不足:微分が y' = 2x になる理由や、微分の定義についてもう少し詳しく説明すると、理解が深まります。
場面描写の不足:公園の風景や季節感、周囲の雰囲気など、背景描写があると物語に深みが出ます。
会話の流れがやや急:少年の疑問から理解に至る過程が急速で、もう少し段階的な説明や少年の反応を描写すると自然になります。
T(Try:次回試してほしい点)
数学的説明の補足:微分の基本的な定義や、導関数の求め方について簡単に触れることで、読者や少年の理解を助けます。
背景描写の充実:五感を使った公園の描写を加え、読者がその場にいるかのような臨場感を生み出してみてください。
会話の深掘り:少年の疑問や納得する過程を詳しく描き、対話にリアリティを持たせると良いでしょう。
K (Keep: Positive Aspects)
Effective explanation through dialogue: The essay uses a conversation between a teacher and a student to explain the abstract concept of differentiation, making it accessible and easy to understand.
Use of specific examples: Utilizing the graph of y = x^2 to visually explain the concept helps readers grasp the idea that zooming in on a curve makes it appear linear.
Clear metaphors: The metaphors of "bird's eye view" and "using a magnifying glass or microscope" effectively convey the difference between seeing the whole picture and focusing on details.
P (Problem: Areas for Improvement)
Lack of mathematical detail: Providing more explanation on why the derivative of y = x^2 is y' = 2x and discussing the definition of differentiation could enhance understanding.
Insufficient setting description: Adding descriptions of the park's scenery, the season, and the surrounding atmosphere would add depth to the narrative.
Abrupt flow in conversation: The boy's progression from confusion to understanding happens quickly; elaborating on his thought process and reactions would make the dialogue feel more natural.
T (Try: Suggestions for Next Time)
Supplement mathematical explanations: Briefly touch upon the basic definition of differentiation and how to find derivatives to aid the reader's and the boy's comprehension.
Enrich background descriptions: Incorporate sensory details about the park to create a vivid and immersive setting for the reader.
Deepen the conversation: Elaborate on the boy's questions and the steps leading to his understanding to add realism to the dialogue.
学ぶ
1. 頻出単語
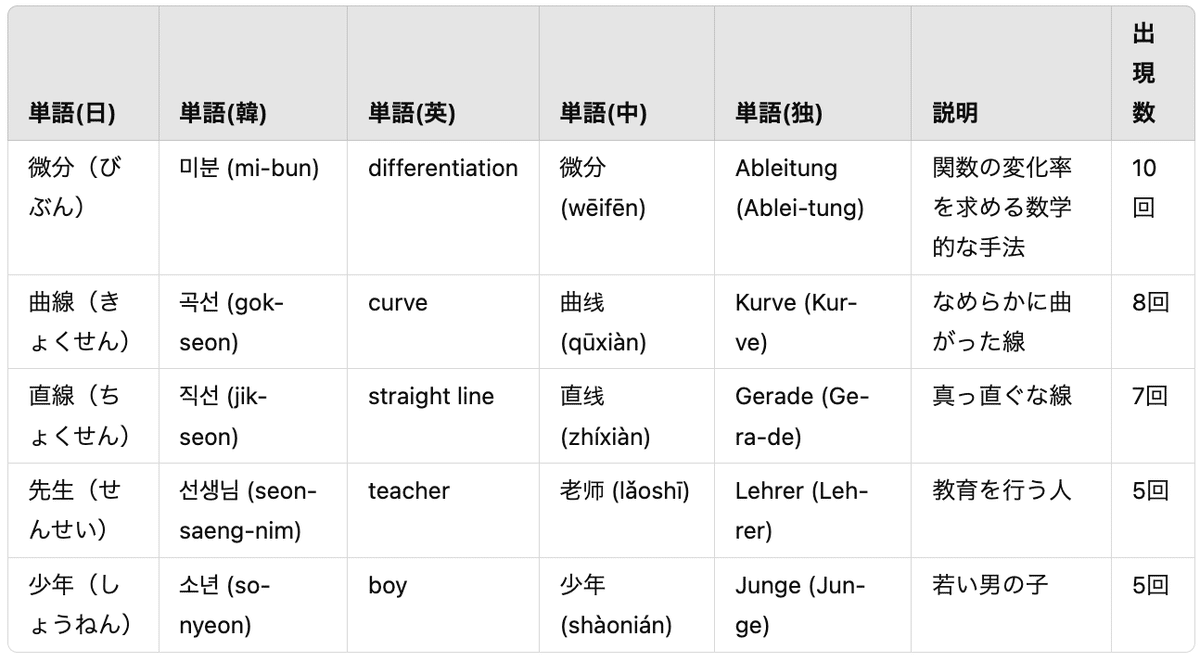
2. 頻出熟語
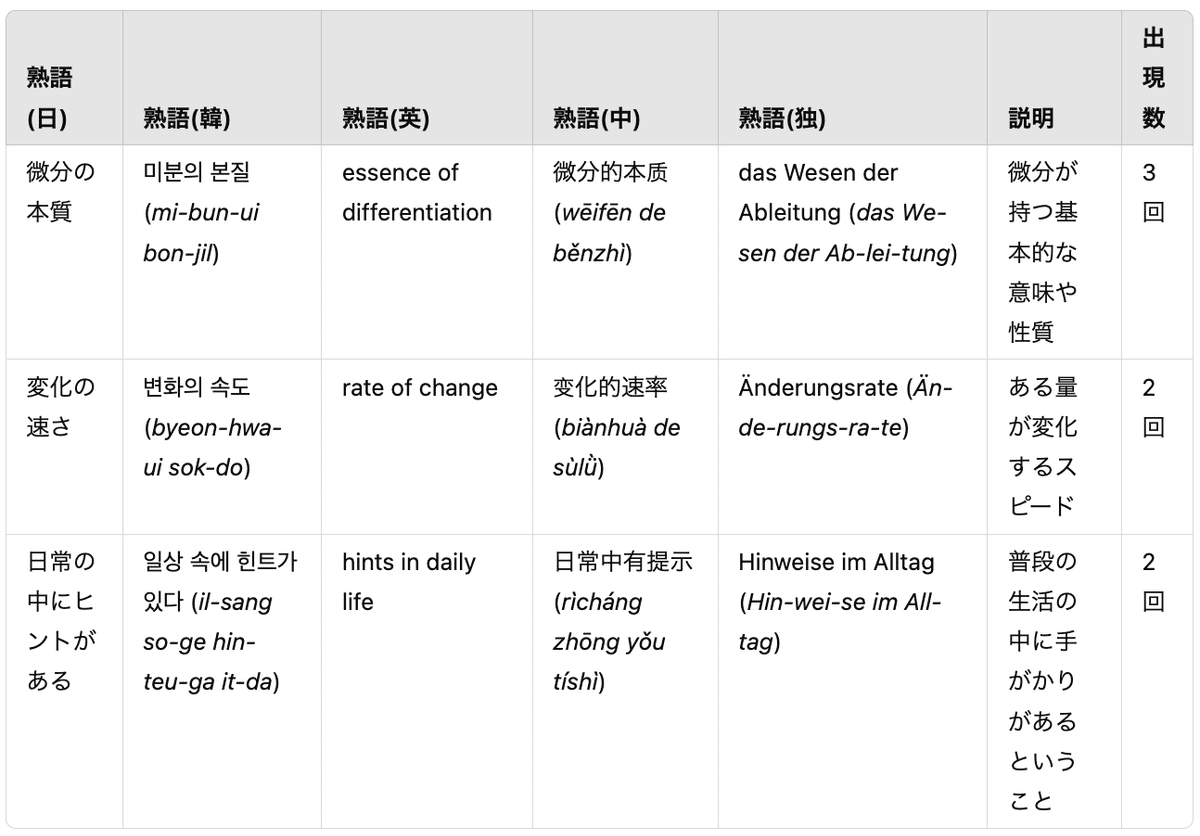
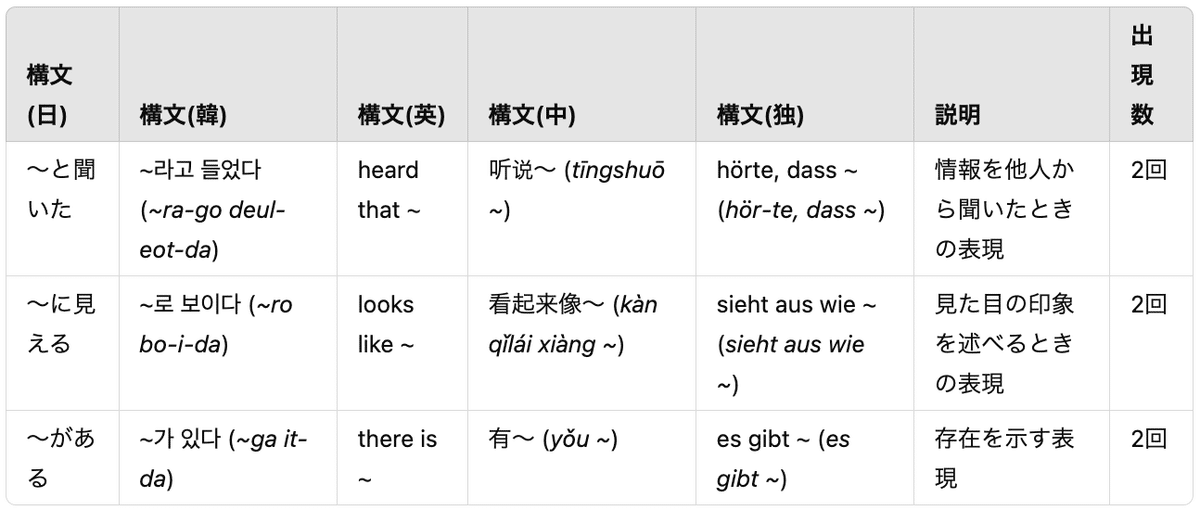
3. 頻出構文