BigQuery ML の多変量時系列モデル(ARIMA_PLUS_XREG)で簡易に施策効果推定を行ってみる

畳屋民也

2023年10月27日 11:05

マネーフォワード CTO室 AI推進部の tamiya です。
好きな Slack 絵文字は :curry_forward: です。

前回の記事では、~~スリランカカレーの布教~~ BigQuery ML（以下 BQML）の概要とどんなときに使えるかについて例を交えて紹介しました。

この記事では、その実例編といった形で、ビジネスでもしばしば出くわす施策効果推定を BQML を用いて簡易的に行う方法について紹介したいと思います。

問題設定

以下のような日毎のアクセス数の時系列データを考えます。
ここでは、3月12日からアクセス数を伸ばすための施策を開始しました。
この施策により、もし施策を行わなかった場合と比べてどれだけアクセス数が増えたかを見ようと思います。

人口的に生成したアクセス数を模した時系列（実線）。3/12から施策介入を行なっている。
参考までに、施策介入による影響を差し引いたアクセス数も点線時系列で載せている。

なお、今回は人工的なデータを作成して実験しました。
CausalImpact の Tutorial を参考に、自己回帰過程(AR(1))をもとにデータ列を生成し、3月12日以降は施策介入効果として期待値10分散2の正規分布に従う乱数を加えました。

library(dplyr)

set.seed(1)

x1 <- 100 + arima.sim(model=list(ar=0.999), n=100)
y_0 <- 1.2 * x1 + rnorm(100)

y_1 <- y_0
y_1[71:100] <- y_1[71:100] + rnorm(30, 10,2)


time.points <- seq.Date(as.Date("2014-01-01"), by=1, length.out=100)

post_start_date <- as.Date("2014-03-12")


data <-data.frame(day=time.points, y1=y_1, y0=y_0)
data <- data %>%
    mutate(is_post=case_when(day>=post_start_date~1, .default = 0))

write.csv(data, "../data/demo_data.csv")

主なカラム内容は以下になります：

day … 日付
y1 … 観測値（実データ）
is_post … 介入有無を 0 or 1 で表したフラグ

BQML の多変量時系列モデル（ARIMA_PLUS_XREG）について

ARIMA_PLUS_XREG は、2023/07/21に GA(Generally Available) になった機能で、ARIMA モデルベースの時系列予測と外部変数による回帰を組み合わせた多変数時系列モデルを作ることができます。

例えば、売上を目的変数にしたモデルに外部変数として気温を加えることで、気温による売上変化を加味した時系列モデルを作ることができます。

今回の場合、アクセス数 (y1) を目的変数としつつ、外部変数として施策介入有無フラグ (is_post) を用いることで、施策介入有無フラグの回帰係数から介入効果を推定することができます。

ARIMA_PLUS_XREG を用いた施策効果推定

モデル作成

それでは早速モデルを作ってみようと思います。

CREATE OR REPLACE MODEL
  `sample-project.sample_dataset.demo_model_for_tamiya_note`
OPTIONS(
    MODEL_TYPE='ARIMA_PLUS_XREG',
    time_series_timestamp_col='day',
    time_series_data_col='y1' ) AS
SELECT
  day,
  y1,
  is_post
FROM
  `sample-project.sample_dataset.demo_timeseries_for_tamiya_note`

作り方は簡単。
CREATE MODEL の OPTIONS として以下の値を指定します：

MODEL_TYPE: "ARIMA_PLUS_XREG"
time_seriese_timestamp_col: 日時カラム名 (今回は `day`)
time_series_data_col: 目的変数カラム名（今回は `y1`）

そのうえで、SELECT 句以下でデータソーステーブル名と必要なカラムを選択します。ここで選択したカラムのうち、上記でパラメータ指定したカラム以外は全て外部変数として扱われます。今回の場合、施策介入有無のフラグ `is_post` が該当します。

他にも細かいオプションはいろいろありますが、基本はこれだけです。
上記のクエリを実行すると、モデルが作成されます。

予測結果の確認

モデル作成が完了したら、予測結果の取得を行います。

`ML.EXPLAIN_FORECAST()` を使うことで、モデルによる予測結果を成分分解したものが得られます。仕様上、最低でも1期先分の予測のための外部変数は与えないといけないことに注意してください。

SELECT
  time_series_timestamp AS day,
  time_series_type,
  time_series_data AS y1,
  time_series_adjusted_data,
  attribution_is_post
FROM
  ML.EXPLAIN_FORECAST(MODEL `sample-project.sample_dataset.demo_model_for_tamiya_note`,
    STRUCT(1 AS horizon),
    (
     SELECT
  DATE("2014-04-11") AS day,
  1 AS is_post
 ))

上記のクエリを実行することで、以下のような結果が得られます：

今回着目するのは、以下のカラムです：

day (time_series_timestamp): 日時
y1 (time_series_data): 実データ（4/11分のみ予測値）
time_series_adjusted_data: 予測値
attribution_is_post: 施策介入有無フラグ (`is_post`) による回帰の寄与成分

このうち、施策介入効果は今回の場合 attribution_is_post になります。
上記では 10.65 と推定されました。

上記のほかにも季節成分、トレンド成分、祝日効果などを取得できる場合もありますが、今回は使いません。

結果の可視化

最後に、施策介入による効果をより詳しく可視化していきたいと思います。
可視化には Looker Studio （旧 Data Portal, Data Studio）を使いました。

まずは、実データと予測値の対応を見てみたいと思います。
予測値は time_series_adjusted_data カラムに入っていますが、これには施策介入による効果も含まれていますので、その分を差し引いた値が「施策介入がなかった場合の仮想的な予測値」となります。

予測値（介入なし）: time_series_adjusted_data - attribution_is_post

これらを図示すると、以下のようになります：

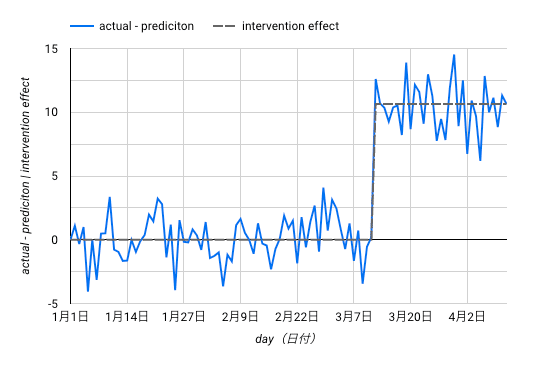
さらに、詳細な施策介入効果を見るために、実データと予測値の差分を見てみます：

詳細な介入効果: y1 - (time_series_adjusted_data - attribution_is_post)

これを、平均的な施策介入効果 (attribution_is_post) とともに図示したものが以下になります。

まとめ

以上のように、ARIMA_PLUS_XREG を使えば、施策介入有無を表すフラグを外部変数として回帰を行うことで、施策効果の推定を簡易に行うことができました。
今回は施策介入有無フラグのみを用いたものの、その他にも複数の変数を同時に盛り込むことも可能です。

ただし、以下の2点には注意する必要があります：

施策介入効果の信頼区間を出せない
- 2023年10月時点では、回帰成分による寄与の信頼区間を出すことができません。
- 一応、線形回帰（`LINEAR_REG`）と組み合わせれば同様のものを出力できるものの、やや手数が増えます。
施策介入効果が時間変化するような場合は対応ができない
- 現状では回帰係数は時間に依存せず一定となるため、施策介入効果が時間とともに減衰するようなケースには対応できません。

したがって、より精緻な推定を行うのであれば、 CausalImpact など状態空間時系列モデルやベイズ推定による手法を用いるのが良いでしょう。

とはいえ、とりあえずデータを BigQuery で集めてみて、推定できそうかのあたりを初手でつけておくという使い方であれば、試してみる余地は十二分にあると考えています。