
無機化学演習-大学院入試問題を中心に-3 章解説
例題3・1
(1)解説参照。 hcp と ccp について覚えておきましょう。また ccp は面心立方格子をとるということも今後の問題を解くにあたって重要な知識です。
(2)
(a)最密充填構造は hcp と ccp の種類に関わらず配位数は 12 です。
(b)面心立方格子に含まれる原子数の求め方は大学受験でやりました。復習してください。また体心立方格子についてもできるようにしましょう。
立方格子の頂点に位置する剛体球は 1/8, 立方格子の面に位置する剛体球は 1/2, 辺に位置する剛体球は 1/4, 立方格子の中心もしくは内部に位置する剛体球は 1 個として数えます。
(c)こちらも大学受験の知識です。格子定数とは立方格子の 1辺の長さのことです。
(d)解説参照。
(3)
(a)解説参照。
(b)答えは 8 です。最密充填構造の hcp と ccp は最近接原子数が 12 ですが体心立方格子は最密充填構造ではありません。体心立方格子の図を見ると中心の原子が 8 個の原子に囲まれていることが分かります。
(c) (2) の(b) と同様です。
(d) 1 Å = 1.0 × 10⁻¹⁰ m = 1.0 × 10⁻⁸ cm です。
よって 0.971 g cm⁻³ × (4.28 × 10⁻⁸ cm)³ の式により立方格子の重さが分かります。立方格子は 2 つの原子により構成されているので原子 1 つの質量は上の式を 2 で割って 3.81 × 10⁻²³ g です。
例題3・2
(a), (b)四面体間隙と八面体間隙の数については教科書の解説に書いてある N 個の最密充填した原子からは、 2N 個の四面体間隙と N 個のはてい面体間隙ができる。という部分を覚えてください。
(c)四面体間隙に入ったイオンが最密充填構造のイオンに接する時正四面体は以下のようになっています。正四面体の頂点から重心までの距離が両者のイオン半径の和 (r + ri) に等しくなっている状態です。

正四面体を作る 4 個の原子は、立方体の 8 個の頂点の内半分を占め、というところでここでいう立方体は立方格子すべてのことではありません。立方格子を8 分割した後の立方体のことです。

正四面体と立方体の重心は一致、数学の問題です。
よって頂点から重心までの距離 (r + ri )が立方格子を 8 分割した後の立方体の対角線の半分に相当します。面心立方格子の 1 辺の長さについては例題3・1 でやりました。大学受験の知識です。
立方格子を 8 分割した後の立方体の対角線の半分というのは汚くて申し訳ありませんが下の図を参照してください。三平方の定理より立方格子の 1 辺の長さを 1 とすると対角線の長さは √3 です。よって p51 の式が成り立ちます。

例題3・3
(1) 解説参照。暗記してください。
(2)塩化ナトリウム型はカチオンとアニオンの配位数がそれぞれ 6、塩化セシウム型はカチオンとアニオンの配位数がそれぞれ 8 となっています。解説にもあるようにイオン半径比によって配位数は変わってきます。
"イオン半径比が小さくなると、一方のイオンが他方のイオンの作る間隙の大きさよりも小さくなり、同じ電荷をもつイオンどうしが接近してしまう。逆にイオン半径比が大きくなると接触するイオンの数が大きな結晶構造をとったほうが有利となる。”
解説に書いてあるこの文章が非常に大事なので丸暗記してください。これをあらわした図が p53 の図 3・7 です。この図も非常に大事なので文と図のセットで覚えるといいでしょう。
このことを知っていて初めて問題で聞かれているイオン半径比の範囲は塩化ナトリウム型と塩化セシウム型の限界イオン半径比であることが分かりますね。限界イオン半径比の求め方については解説を見れば十分理解可能なはずです。
(3)解説参照。
例題3・4
以下の図を見れば解けなかった人も理解できると思います。空間図形が得意な人は簡単に解けたのではないでしょうか。

解説に書いてあることは入試には必要ない高度な知識も含まれています。一方で重要な知識もあるのでそこだけ紹介します。
ペロブスカイト型構造は院試でも頻出ですがこの教科書ではあまり触れられていません。 ABO₃ だけでも覚えておきましょう。
またスピネル型の構造について解説 3 段落目で A イオンは四面体間隙の~と書いてある部分があります。これは 6 章でも必要な知識なので覚えてください。
例題3・5
解説の通りです。生成エンタルピー、昇化エンタルピー、などなど各種エネルギーの向きはほぼすべての問題で同じです。ボルンハーバーサイクルはこれ以外のパターンが出題されることは珍しいです。解説の図を覚えましょう。
④の塩素分子の解離ですが 1/2 Cl₂→ Cl のところで 1/2 がついているので個人的には与えられたエネルギーを 2 で割るのが正解なのではと思います。実際に章末問題 3・18 では塩素の解離エンタルピーが 2 で割られています。例題では 122 kJ/mol, 章末問題では 121 kJ/mol と近い値になっていますからおそらく例題の解説が間違えています。
例題3・6
(1)解説参照。非常に重要です。
(2)解説のようにいきなり微分しようと思いつく人は少ないと思います。いたとしたら東工大や東大の内部生の方でしょう。この問題はできなくてもいいですが導出された Born-Mayer の式自体はよく院試に出てくるので d と d₀などややこしいところもありますが絶対に暗記してください。
(3)解説参照。各値をBorn-Mayer の式に代入してください。Born-Mayer 式はイオンをすべて電荷として計算しているため原子間に共有結合的な~値からずれることになる。という部分が非常に重要です。院試の過去問でよく見かけます。
例題3・7
解説参照。
例題3・8
かなりの難問です。この教科書では説明が不十分ですし他のコットンガウスウィルキンソン無機化学、シュライバーアトキンス無機化学のような分厚いでも満足のいく解説は載っていません。またこの構造因子に関する問題は院試ではあまり見ません。
1,2 段落目は分析法の原理です。 3 段落目からが重要です。面指数(ミラー指数)については図で解説します。
結晶における反射面を表すのに面指数 (hkl) が用いられる。これは結晶の三つの格子ベクトルに対してそれぞれ 1/h, 1/k, 1/l の点を通る平面を表している。とあります。以下に具体例を示します。

斜線で塗られた面が反射面です。教科書 p60 の反射面と書かれた図を見てください。反射面はいくつかあります。ある面で反射した光と別の面で反射した光の経路差が波長の整数倍になった時に波が強い干渉を起こして回折像が得られるのです。

研究室で単結晶 X 線解析をしたことがある人にはおなじみかもしれませんが上図の点の部分が X 線が強め合った結果えられた回折像です。ブラッグの式は大丈夫でしょうか。高校物理でやった経路差の問題の中では最も単純なものの一つだと思います。わからない方はしっかりと復習してください。
面間隔 d とh, k, l の式は必ずどちらも覚えてください。特に立方晶の式はよく問われます。斜方晶とは立方格子の 3 辺の長さがすべて異なるもの、立方晶とは立方格子の辺の長さがすべて等しいものです。
ここからが本題です。 p61 の単位格子内に~というところの解説です。ここでいきなりΨhkl = 2π (hx + ky + lz)と構造因子の式が現れて混乱すると思います。この部分はどうしても理解したいという人以外は式を丸暗記しましょう。
どうしても知りたいという人向けに説明すると()内部はベクトルの計算です。早めに書けばよかったのですがh, k, l は教科書の表記で斜め文字(イタリック)ですからベクトルを表しています。そのことが分かれば()の中身については理系大学生の皆さんなら大丈夫でしょう。以下に構造因子の式の導出の分かりやすい資料を共有します。
http://uc-garden.dyndns.org/testprint/webpri/TeX/ssp2_fixed.pdf
体心立方格子の (1/2, 1/2, 1/2)にある同じ散乱因子を持つ原子とは中心の原子です。体心立方格子に含まれる原子数を求める問題を思い出すと格子の頂点に位置する原子の剛体球は 1/8, 格子の中心に存在する原子は 1 として数えました。それと同じことで結晶格子の頂点にある原子は 1/8 f, 中心の原子は f の散乱因子を持つとしています。
(1/2, 1/2, 1/2)がベクトルではなく座標であることに注意して式変形すると以下のようになります。
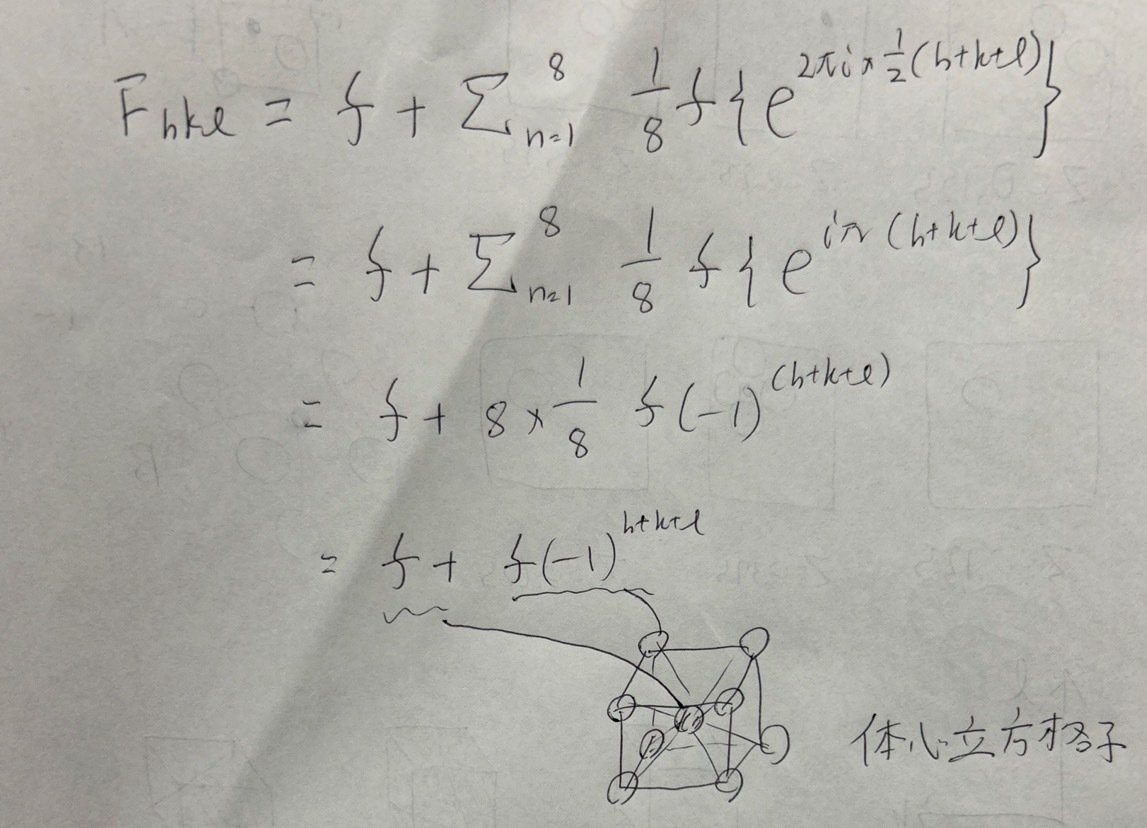
p 61 に反射の強度は構造因子の絶対値の二乗に比例するとあります。問題を思い出すとブラッグ反射の起こる条件ですから構造因子が 0 にならなけらばいいですね。よって h+k+l が偶数の場合にのみブラッグ反射が起こることが分かります。
3・1
p 61 のdhkl=a/√h²+ k² + l² の式にh=1, k=1, l=1 を代入します。
3・2
単純立方格子の結晶の(111)面の面間隔 d は 3・1 で求めました。銅は面心立方格子ですから解説にあるように a=2√2 rです。
d=√3/3 aに a=2√2 rを代入すると答えになります。

八面体間隙は無視してください。面心立方構造の(111)面を 2 つ書きました。この面の間隔が上下に積み重なった最密充填層間の距離に等しいのです。
3・3
単位格子の頂点にある剛体球は 1/8 個、辺にある剛体球は 1/4 個、面に位置する剛体球は 1/2 個、格子内部は 1 個として数えると単位格子に含まれる炭素原子の数が 4 つだとわかります。
解説にある炭素原子間距離 a は平行四辺形の一辺である点線ではなく正六角形の一辺です。平行四辺形の一辺の長さは √3a です。求め方は下の図を参照してください。

次に単位格子の体積を求めます。底面積は一辺が √3a, 高さが 3/2 a で、単位格子自体の高さは 2b です。よってこれらをすべてかけて単位格子の体積は 3√3 a²b となります。

密度計算は以下の通り

3・4
NaCl は塩化ナトリウム型、CuCl は閃亜鉛鉱型、CsCl は塩化セシウム型でカチオンとアニオンの配位数はそれぞれ (6,6), (4,4), (8,8) です。この 3 つの型だけでなく蛍石型、ウルツ鉱型、逆蛍石型など他の構造も配位数と陽イオンの数、陰イオンの数を言えるように、そして構造の絵を書けるようにしましょう。
イオン半径についてですが例題 3・3 の p53 の図 3・7 を見てください。配位数が小さくなるほどイオン半径比(陽イオン半径/陰イオン半径)が小さくなることが分かります。NaCl, CuCl, CsCl のすべてで陰イオンは Cl⁻ で固定されているので金属陽イオンのイオン半径は配位数が大きい順になります。
3・5
立方晶、正方晶などの見分け方については以下のリンクやシュライバーアトキンス無機化学に乗っているのでそちらを参照してください。
3・6
蛍石型の配位数や構造は各自確認してください。逆蛍石型もついでに確認しましょう。
3・7
マーデルング定数は結晶構造の形によってのみ決まる定数です。塩化ナトリウムと塩化カリウムは同じ塩化ナトリウム型の結晶構造をとりますからマーデルング定数は同じです。
Born-Mayer 式は p 57 (2)の答えです。この式の d₀=rx+ry は隣接する陽イオンと陰イオンの中心距離、 d は短距離のイオン間反発を示す定数であることに注意しましょう。このことに気を付けると 1/d₀(1-d/d₀)だけに着目して式を解けばいいことになります。あとは各値を代入しましょう。
3・8
結晶格子の頂点にある原子は 1/8f, 中心の原子は f の散乱因子を持つとして計算しています。例題 3・8を参照してください。
3・9
(1)解説参照。
(2)面心立方格子には原子が 4 つ含まれるので 4 をかけるのを忘れないようにしてください。
3・10
解説参照。p 50 で四面体間隙と八面体間隙の位置を確認しておいてください。
3・11
(1)立法格子の頂点に位置する剛体球は 1/8 個、辺に位置する剛体球は 1/4 個(今回はありません)、面に位置する剛体球は 1/2 個、立方格子内に存在する剛体球は 1 個として数えます。
(2)密度は 3・10 と同様に計算してください。次に Sn 原子間の結合距離についてです。ややこしいですが例題 3・2 を参照してください。正四面体と立方体の重心は一致するので結合距離(頂点から重心までの距離)は立方体の対角線の半分、つまり面心立方格子の対角線の1/4 となります。詳しい回折は例題 3・2 にあります。
(3) 前問まではβ-スズについての問題でした。ここからはα-スズについての問題です。β-スズでは単位格子中に 8 個の原子がありましたが問題文よりα-スズには 4 つの原子が単位格子中に含まれています。立方格子1 個が正方格子 2 個に相当するというのはここに由来します。
(4)解説参照。
3・12
解説参照。
3・13
単純な体心立方格子の計算問題です。以下に体心立方格子の 1 辺と原子間距離の関係を示します。今回は原子半径が r ではなく原子間距離が r ということに注意してください。原子間距離とは分子内の2 つの原子核間の距離です

手計算では不可能でしょう。
3・14
解説参照。
3・15
AgI の結晶構造は問題文にあるように閃亜鉛鉱型の結晶構造を書きましょう。
この問題はそもそも六方格子を持つ氷の安定面は 3 回対称性を持っていることと面心立方格子の対角線が 3 回回転軸を持つことを知っていなければ解けないでしょう。
3 回対称性とは点群を勉強した人にとってはわかりやすいかもしれません。簡単に言うと 120 度回転させたときに回転させる前と同じとみなせるということです。 4 回対称性だったら 90 度、 2 回対称性だったら 180 度です。
問題文にあるように氷と AgI のある面の対称性があっていることから AgI の3回対称性を持つ面が答えになるわけですがそれは 3 回回転軸である面心立方格子の対角線と垂直な面です。つまり(1,1,1) 面となります。
ミラー指数(面指数については例題3・8 を参照してください。
3・16
解説参照。
3・17
(1)下の図を参照。

(2)代入するだけです。
3・18
例題 3・5 と同パターンです。そちらを参照。
3・19
例題 3・5 の解説に同様のことが書いてあります。
3・20
マーデルング定数は例題 3・6 で出てきましたがこの問題を解けるほどマーデルング定数についての解説がありませんでした。マーデルング定数ん計算については以下のリンクが分かりやすいです。一次元鎖の部分も飛ばさないでください。
陽イオンに対する第一隣接イオンとその距離については以下の図を見てください。*印をつけたナトリウムイオンから見て第一隣接イオン、第二隣接イオン、という風にしています。もちろんどのナトリウムイオンからみても隣接イオンの個数と距離は変わりません。

さて、解説にある計算ですがこちらは静電エネルギーの計算をしています。マイナスやプラスはそのイオンの電荷によって変わります。静電エネルギーの計算ですがV=ke²/r, もしくは V=e²/4πεr でした。r は距離、k と εは定数です。
e²/4πεrの部分が計算結果から消えていますがそれは 教科書 p57 のボルンマイヤーの式のマーデルング定数の部分だけを抜き出しているからです。ボルンマイヤーの式に e²/4πεr が入っているのが分かります。d と r で違いますが距離なので同じです。マーデルング定数はボルンマイヤーの式の A の部分だけであることを忘れないでください。
3・21
逆格子ベクトルが分からなければ解けません。逆格子ベクトルの解説は以下のリンクに任せます。捨てていい問題かもしれません。
3・22
(1) 解説参照。
(2)
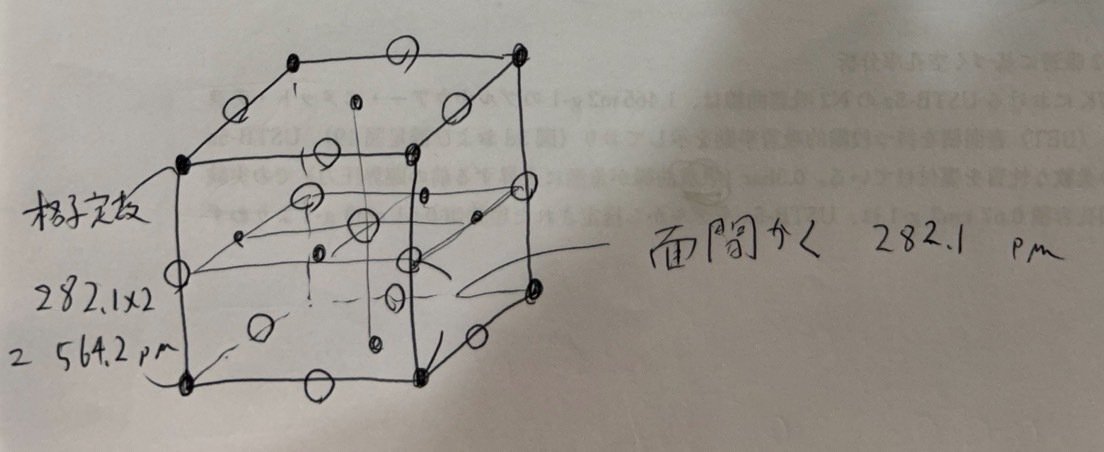
公式に当てはめてください。
(3) 体心立方格子の場合(例題 3・8 ) 同様に計算すると面心立方格子の構造因子が解説のようになります。
(4)解説参照。
この記事が気に入ったらサポートをしてみませんか?
