【公理・定義・定理】正しく使い分けれますか？

　こんにちは〜インフラエンジニアのtamolabです！
皆さん、特に大学受験生と学校の数学教員！！！公理、定義、定理をちゃんと理解できていますか？今日は公理、定義、定理の違いを数学が苦手な人に対しても説明していきたいと思います！

1. 公理・定義・定理

【公理】

「公理」とは、正しいと証明せずに、正しいものとして使いましょうという数学をする人の間の約束です。例えば下記のようなものも公理です。

公理の例
　本noteの読者は、読日本語の文章を理解できるものとする。

【定義】

「定義」とは、議論を進めるために人が勝手に作った取り決めを記したものです。例えば下記のようなものは定義です。

定義の例
　"偶数"とは2の倍数である。

【定理】

「定理」とは、公理から導き出され、定義された言葉のみで構成された正しいことが証明できる文章です。例えば下記のようなものは定理になります。定理はいくつかの定義をで証明することができます。下記の例では、先のどの定義（"偶数"とは2の倍数である。）を利用することで、下記の主張が正しいことを証明することができます。

定理の例
　4の倍数は"偶数"である。

2. 代表的な題材

この例題は、私が教育実習で高校数学を担当したときにも実際に題材にしました。

指数法則とその拡張は「定義」を理解する上で有効的です！

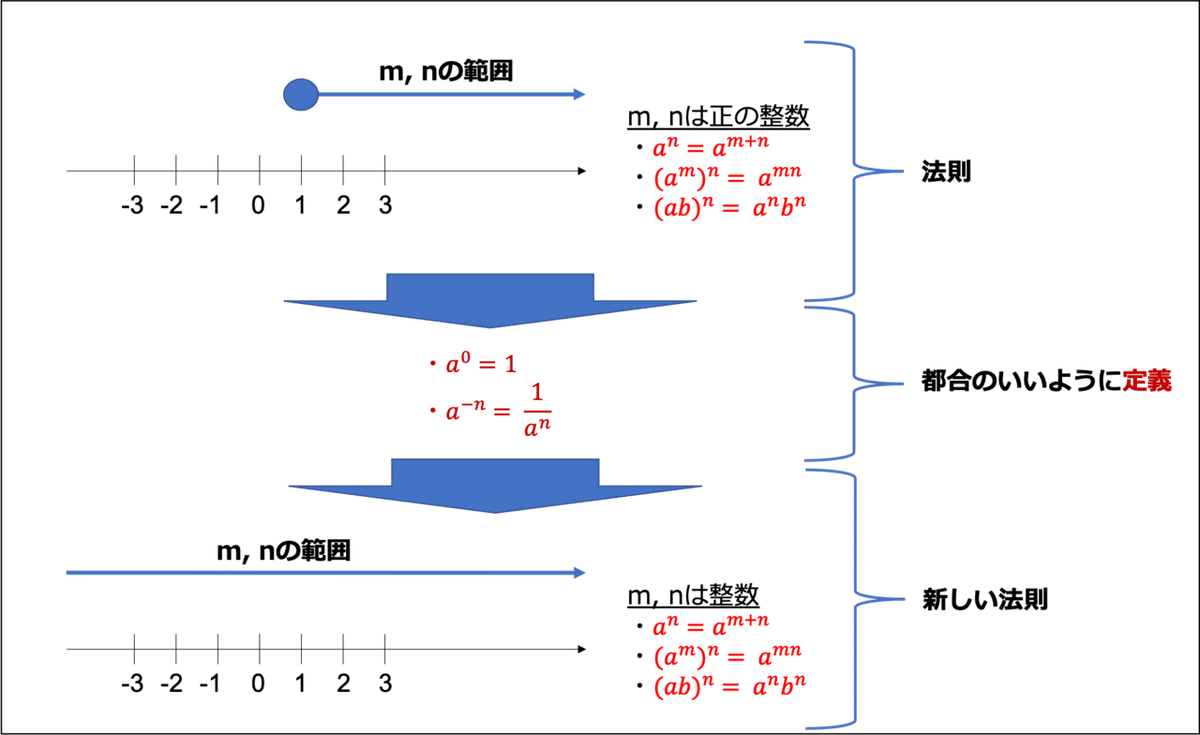
じゃあ、m, nが有理数のときは？実数のときは？と議論が広がっていきます。議論を展開するにあたって、いくつか都合がいいように定義をすることで新たな法則や定理が生まれてきます。上の図で言うと、「法則」に都合のいいような「定義」を加えることで、新たな「法則」が見つかります。もちろん、「新しい法則」は既存の「法則」と「都合のいいうように定義」した内容で説明（証明）することができます。

キーワード

#定義 #定理 #公理 #指数法則 #数学

お問い合わせ

　本投稿のコメントでも構いませんし、下記からお問い合わせいただいても大丈夫です。
　note.tamolab@gmail.com