
【写像】数列って単純な写像だよね
こんにちは〜インフラエンジニアのtamolabです!数列って単純な写像だよね(タイトル回収)。
それだけが言いたかったことです。笑 高校数学で数列の一般式とかその和とか出してたけど、写像の勉強をしていて単なる写像だと認識しました。数列も二次関数とかの関数と同じなんですよね。という話をしていきたいと思います。。が今回は写像のお話をします。
1. 写像とは

写像とは、二つの集合A、Bが存在し、Aの各要素aにBの一つの要素bを対応させる規則fをAからBへの写像といいf:A→Bと表します。

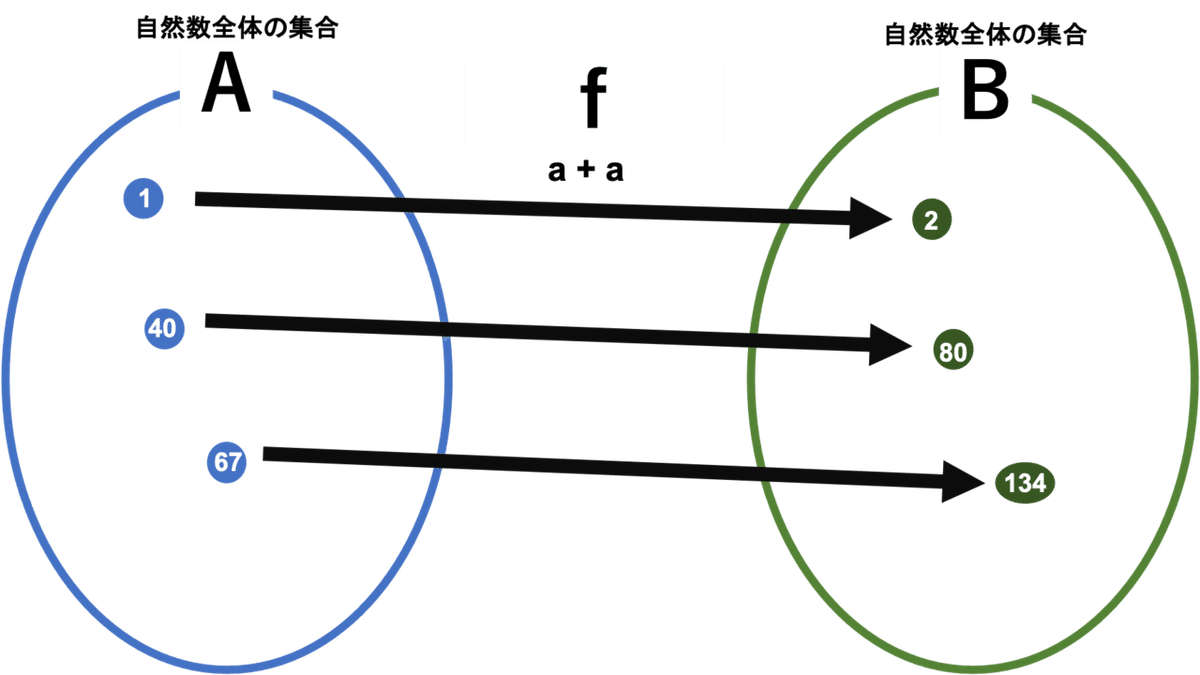
はい。何言ってるかわからないですね笑 簡単に言えば、集合A, Bを自然数全体とし、対応させる規則fをa+a(加法法則)とするとき、a+aが必ずBの集合になればfはAからBへの写像というわけです。(簡単ではなかった)
数学の面白いところは、上の+についてもちゃんと加法法則、いわゆる足し算であると説明しないと、突っ込まれる点ですね笑
下記のような対応規則fの場合は、Aの各要素に対してBに収まらないので、fはA,Bの写像であるとは言えないのです。

写像の正確な表記は下記のように表現します。

上記を日本語で訳すと、「自然数全体の二つの始集合と終集合に対し、対応させる規則fをa+a(加法法則)とする」と書いていますね笑
関数は (定義域や終域が数や数ベクトルの集合という) 特別な写像です。中学校でも習う関数は、x(定義域)に対してy(値域)が存在しますね。xを一つ定めたらyが一生見つからないという事態にはならないと思います。それは中学・高校数学で利用される関数というのは、既に写像である条件を満たしているものばかり扱うからです。こういう点が高校数学と大学数学の違いですよね。今まで当たり前であったことが当たり前でなくなる感じです笑なので、高校数学では安心してxを決めてyを見つけてください笑
2. キーワード

3. お問い合わせ

本投稿のコメントでも構いませんし、下記からお問い合わせいただいても大丈夫です。
note.tamolab@gmail.com
いいなと思ったら応援しよう!

