231014 つくってあそぼ~GSH (glutathione) 合成に関する酵素反応のモデル~
はじめに
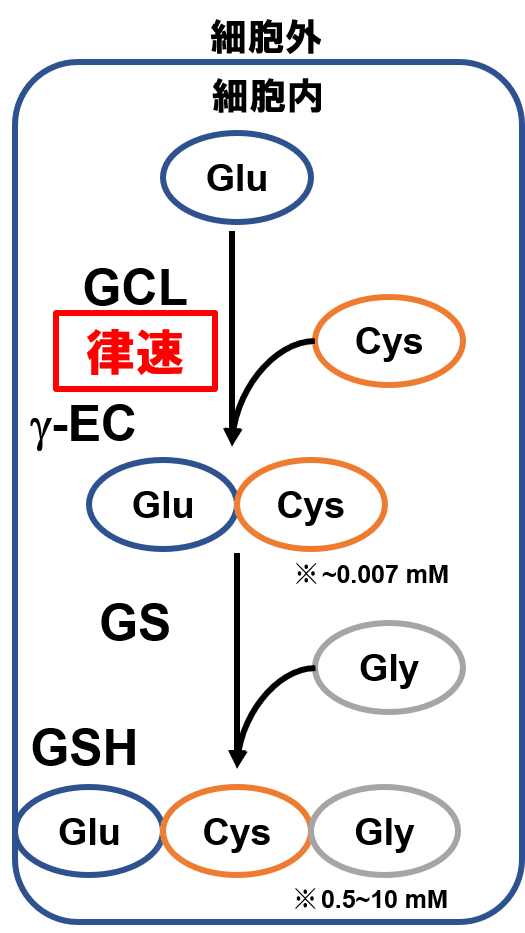
GSH (glutathione) は活性酸素種の消去や還元力の提供など,細胞内で重要な役割を担うトリペプチドである.トリペプチドである GSH は構成アミノ酸三種が二回重合することで生じる.具体的に生合成経路は下記二段階から成る.
Glu + Cys +ATP → γ-EC + ADP + Pi
γ-EC + Gly + ATP → GSH + ADP + Pi
第一段階を触媒するのが GCL (g-glutamyl cysteine ligase),第二段階を触媒するのが GS (Glutathione synthetase) である.このうち律速・制御段階となるのは,多くの生合成反応と同様に出発反応である第一段階である.
Fig. 1 に示す通り,ヒト細胞内では中間体 γ-EC はほとんど存在せず,細胞内のチオールは主に GSH の形で蓄積されている.これはヒト以外の多くの生物種でも同様であり,GCL が制御酵素であるだけでなく元々の活性が大きく異なることによると思われる.
今回はシロイヌナズナの GCL, GS の酵素学的パラメーターを調べた論文をもとに GSH 合成反応のモデルを作って遊びたいと思う.まずモデルをつくるための酵素反応速度式について学び,その後実際のモデルを作ってみよう.
反応速度式① Michaelis-Menten 式
高校~大学初級で習う酵素反応速度式といえば Michaelis-Menten 式である.これは酵素 $${(E)}$$ が基質 $${(S)}$$ と結合し,酵素基質複合体 $${(C)}$$ を形成したのち $${E}$$ から生成物 $${(P)}$$ が遊離する機構で進行する反応の速度を示すものである.
$${E + S \rightleftarrows C \rightarrow E + P}$$
このとき全体の反応速度は最大反応速度 $${V_{max}}$$ とミカエリス定数 $${K_M}$$ を用いて次のように表される (導出略).
$${v = \cfrac{V_{max}}{K_M + [S]}}$$
これだけでも結構厄介なので生化学の授業では躓きがちであるが,代謝産物だけ見ると基質一分子から生成物一分子のみが生じるというかなり単純化されたモデルであることがわかる.
$${S \rightarrow P}$$
Michaelis と Menten はインベルターゼ (ショ糖の加水分解酵素) を十分希薄な水溶液中で反応させることにより擬一次反応とし,モデルの単純化に成功したわけであるが,実際の酵素反応は多くが多基質多生成物反応である.実際に上述の GCL, GS 触媒反応はいずれも三基質三生成物反応であり,このモデルでは GSH 合成速度を確認することができない.そこで,Michaelis-Menten 式を多基質多生成物反応へ拡張した場合について学んでみよう.
反応速度式② 多基質多生成物反応速度式
多基質多生成物反応の分類
多基質多生成物反応は大別して下記の二種からなる.
Random reaction
Ordered reaction
Random reaction は酵素と基質の結合順に決まりがない反応であり,Ordered reaction は酵素と基質の結合順が決まっている反応である.
Ordered reaction は酵素と基質ないし生成物の結合・遊離の順番に基づき,さらに Sequential reaction と Ping-pong reaction に分けられる (詳細は後述).

こうした反応機構名のあとに基質と生成物の数を接頭辞を用いて示すこともある.例えば Ping-pong 機構により進行する二基質二生成物反応の場合は Ping-pong-Bi-Bi 反応,Sequential 機構により進行する三基質二生成物の反応は Sequential-Tert-Bi 反応といった具合である.
酵素反応に関する定量的研究の過程でこうした中間体の生じる順序を簡便に記載する方法が求められ,Cleland の提案した記法が広く受け入れられたため,まず Cleland の記法について概説する.
なお結論から言うと GCL も GS も Ping-pong 反応を触媒するので,Sequential 反応や Random 反応の説明はオマケである.
Cleland の記法~Michaelis-Menten 式を例に~
上述の通り,酵素上に結合ないし遊離する基質・生成物の順序を正確に理解する必要がある.通常の反応式でこれらを表現すると煩雑になるため,Cleland が提案した記法が現在広く用いられている.後々のために Cleland の記法を導入し,例として Michaelis-Menten 式を挙げて説明する.
まず水平に線を引き,これを酵素表面に見立てる
酵素に結合する場合は上から下へ矢印を引くことを,酵素から遊離する場合は下から上へ矢印を引くことを基本とし (例外アリ),左から右に時間が流れるものとする
反応速度定数は矢印の横に書き,酵素の状態を酵素表面に見立てた線の下に書く.
中間体は () に入れて表すことが多い

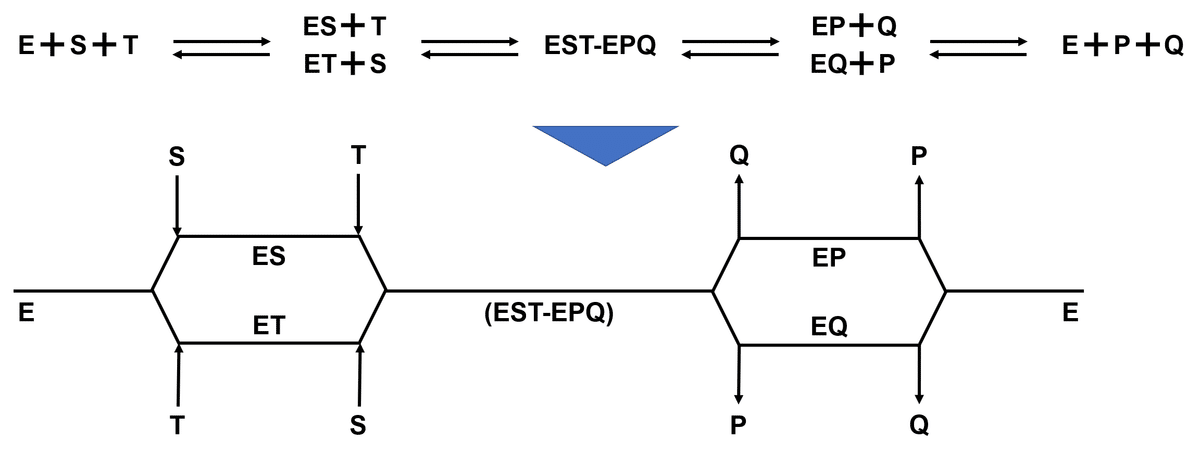
Ordered reaction① Sequential-Bi-Bi 反応
以下では簡単のために,二基質二生成物反応に限って議論する.
Sequential-Bi-Bi 反応とは酵素表面上に決まった順番で基質が結合し,酵素基質三複合体を形成したのち,同じく決まった順番で生成物の遊離が生じる反応機構を指す.
酵素 $${E}$$ 上で二種の基質 $${S}$$, $${T}$$ から二種の生成物 $${P}$$, $${Q}$$ が生じる反応が起こるとき,Sequential-Bi-Bi 反応では必ず以下の順で反応が進行する.
一番目の基質 $${S}$$ が $${E}$$ に結合し複合体 $${ES}$$ を形成する
二番目の基質 $${T}$$ が $${ES}$$ に結合し酵素基質三複合体 $${EST}$$ を形成する
酵素表面上で反応が進行し酵素生成物三複合体 $${EPQ}$$ となる
$${EPQ}$$ から一番目の生成物 $${P}$$ が遊離する
$${EQ}$$ から二番目の生成物 $${Q}$$ が遊離する
反応式で表すと次のようになる
$${E + S + T \rightleftarrows ES + T \rightleftarrows EST-EPQ \rightarrow EQ + P \rightarrow E + P +Q}$$
Cleland の記法で表すと下図のとおりである.

Ordered reaction② Ping-pong-Bi-Bi 反応
以下では簡単のために二基質二生成物反応に限って議論する.
Ping-pong-Bi-Bi 反応とは酵素表面上で基質の結合と生成物の遊離が交互に起こるような機構で進行する反応を指す.
酵素 $${E}$$ 上で二種の基質 $${S}$$, $${T}$$ から二種の生成物 $${P}$$, $${Q}$$ が生じる反応が起こるとき,Ping-pong-Bi-Bi 反応では必ず以下の順で反応が進行する.
一番目の基質 $${S}$$ が酵素 $${E}$$ と結合し複合体 $${C_1}$$ を形成する.
$${C_1}$$ 上で反応が進行し一番目の生成物 $${P}$$ が遊離し,反応中間酵素 $${E'}$$ が残る.
二番目の基質 $${T}$$ が $${E'}$$ に結合し複合体 $${C_2}$$ を形成する.
$${C_2}$$ 上で反応が進行し二番目の生成物 $${Q}$$ が遊離するとともに $${E}$$ が再生する.
反応式で表すと次のとおりである.
$${E + S + T \rightleftarrows C_1 + T \rightleftarrows E' + P + T \rightleftarrows C_2 + P \rightleftarrows E + P + Q}$$
Cleland の記法で表すと下図 Fig. 5 のとおりである.基質と生成物が酵素表面上で卓球 (ping-pong) のように行きかっており Ping-pong 反応という名前の由来がよくわかる.

片方の基質だけ単独で反応するというのが (個人的には) ややわかりにくいため,ここで具体例として GSH を分解できる数少ない酵素である GGT (Gamma-Glutamyl Transferase) を例にもう少し詳細に説明しよう.GGT はヒトが持つ酵素としてはグルタミン酸 γ 位のペプチド結合 (γ-glutamyl peptide 結合) を加水分解できるほぼ唯一のものであり,その反応機構は以下のようになる.
γ-Glutamyl peptide (以下 γ-Glu-D と省略) の γ 位ペプチド結合に GGT 活性中心の Thr 残基が求核攻撃する
γ-Glu-D-GGT 複合体が中間体 ($${C_1}$$) として形成
D (GSH の場合は Cys-Gly) が遊離し,γ-Glu-GGT が反応中間酵素 (E') として残る
γ-Glu-GGT の γ 位エステル結合に求核剤 A (加水分解の場合は $${H_2O}$$ ) が求核攻撃
γ-Glu-GGT-A が中間体 ($${C_2}$$) として形成
$${C_2}$$ から γ-Glu-A (A が $${H_2O}$$ の場合,単独の Glu) が遊離し GGT が再生する.

なお余談であるが D とか A とかややこしい表記をしているのは GGT が本質的には加水分解酵素というよりは (transferase の名の通り) 転移酵素であるため,γ-glutamyl 基を渡す (Donor) 基質と γ-glutamyl 基を受け取る (Acceptor) 基質という表現が一般的だからである.下図 (Fig. 7) に Fig. 6 を大幅に簡略化した図を示すが,これを見ると D 基質から A 基質への γ-Glu 基の受け渡しが反応の本質であるのがわかりやすい.
なお,加水分解酵素のほとんどが GGT と同じく Thr または Ser を活性中心としており,これらも ping-pong 機構で進行する.

Ping-pong 機構で進行する反応の速度は最大反応速度 $${V_{max}}$$, 基質 $${S}$$ のミカエリス定数 $${K_{M, S}}$$,基質 $${T}$$ のミカエリス定数 $${K_{M, T}}$$ を用いて次のように表される (導出略).
$${v = \cfrac{V_{max}}{1+\cfrac{K_{M, S}}{[S]}+\cfrac{K_{M, T}}{[T]}}}$$
Random reaction Random-Bi-Bi 反応
以下では簡単のために二基質二生成物反応に限って議論する.
Random-Bi-BI 反応は Ordered 反応と逆で基質の結合順を問わない反応であるが,Sequential 機構と同様に酵素基質三複合体は必ず形成する.その反応は以下のとおりである.
酵素 E に基質 S または T が結合し複合体 ES または ET を形成する
ES または ET にそれぞれ T または S が結合し,酵素基質三複合体 EST を形成する
EST 上で反応が進行し,酵素生成物三複合体 EPQ に変化する
EPQ から P または Q が遊離し EQ または EP となる
EQ または EP から Q または P が遊離し E が再生する
反応式に場合分けが発生するためかなりややこしい,下図 (Fig. 8) に反応式と Cleland の表記の両方を示す.Cleland の記法を導入した際に
酵素に結合する場合は上から下へ矢印を引くことを,酵素から遊離する場合は下から上へ矢印を引くことを基本とし (例外アリ)
とした例外がコレである.Cleland の記法では場合分けが発生すると島のように六角形の中を酵素とし,外をバルク溶液側と見なすので上下だけ見ると出入りが逆になることがある.そこまで非直感的ではないのでまぁしょうがないというところだろう.
GCL 反応系の推移予測
ではまず GCL による γ-EC 合成系を試験管で作ったらどれくらいの速度で γ-EC が生産されるのか見てみよう.J. M. Jez らの研究チームがシロイヌナズナの GCL について酵素学的パラメーターを調べており,この際反応機構も調査している.結論としてはすでに述べた通り GCL, GS とも ping-pong-tert-tert 反応であり, GCL の反応速度式は次の通りと報告されている.
$${v_{GCL}=\cfrac{V_{max}\cfrac{[Glu][Cys][ATP]}{abcK_{Glu}K_{Cys}K_{ATP}}}{1+\cfrac{[Glu]}{K_{Glu}}+\cfrac{[Cys]}{K_{Cys}}+\cfrac{[ATP]}{K_{ATP}}+\cfrac{[Glu][Cys]}{aK_{Glu}K_{Cys}}+\cfrac{[Glu][ATP]}{bK_{Glu}K_{ATP}}+\cfrac{[Cys][ATP]}{cK_{Cys}K_{ATP}}+\cfrac{[Glu][Cys][ATP]}{abcK_{Glu}K_{Cys}K_{ATP}}}}$$
ただし $${V_{max}}$$ は各酵素の最大反応速度を,$${K_x}$$ は各酵素の基質 $${x}$$ についてのミカエリス定数を,$${a, b, c}$$ は基質についての補正係数を示している.
$${V_{max}, K_x}$$ についてもきちんと調べられているのだが,とりあえず適当な値を入れて遊んでみる.仮に $${V_{max}=1}$$ mmol / min / mg, $${K_{Glu}=K_{Cys}=K_{ATP}=0.5}$$ mM, $${a=b=c=1}$$ だったとして,基質初濃度 $${[Glu]_0=[Cys]_0=5}$$ mM, $${[ATP]_0=10}$$ mM, 酵素濃度 1 mg \L だったとすると γ-EC はどれくらいの速度で生産されるだろうか?

左が系中の化合物濃度,右が酵素反応速度の時間変化をそれぞれ示している.
なんと約 10 分で反応が完全に進行することになる.これは優秀だ.しかし,冒頭で述べた通り GCL 触媒反応は律速段階にあたるのでこんなに早いわけはない.上記の論文で得られた値をそれぞれ代入して再計算してみよう.
論文で実験的に確認された値である $${V_{max}=0.225}$$ mmol / min / mg, $${K_{Glu}= 95}$$ mM, $${K_{Cys}=5.7}$$ mM, $${K_{ATP}=6.4}$$ mM, $${a=0.063, b=0.38, c=1.7}$$ を代入し,基質初濃度 $${[Glu]_0=[Cys_0]=5}$$ mM, $${[ATP]_0=10}$$ mM, 酵素濃度 1 mg \L だったとすると γ-EC はどれくらいの速度で生産されるだろうか?

左が系中の化合物濃度,右が酵素反応速度の時間変化をそれぞれ示している.
500 min 経過で収率約 95% である,反応速度もかなり早期に頭打ちになっている様子が見て取れる.これはミカエリス定数,とりわけ $${K_{Glu}}$$ が非常に大きいことに由来する.生体内の条件において GCL 触媒反応の律速基質は Cys なのだが,このようにリアクターにすると $${K_M}$$ が直接的に反応速度に効いてくる.
GS 反応系の推移予測
続いて,GCL 反応系によって得られた γ-EC に Gly を付加し GSH を合成する反応系を試験管内で作るとどれくらいの速度で GSH が生産できるか調べてみよう.GCL と同じく J. M. Jez らの研究チームがシロイヌナズナの GS についても酵素学的パラメーターと反応機構も調査している.すでに述べた通り GS も ping-pong-tert-tert 反応であり, 反応速度式は次の通りと報告されている.
$${v_{GS}=\cfrac{V_{max}\cfrac{[ATP][Gly][\gamma EC]}{abcK_{ATP}K_{Gly}K_{\gamma EC}}}{1+\cfrac{[ATP]}{K_{ATP}}+\cfrac{[Gly]}{K_{Gly}}+\cfrac{[\gamma EC]}{K_{\gamma EC}}+\cfrac{[ATP][Gly]}{cK_{ATP}K_{Gly}}+\cfrac{[ATP][\gamma EC]}{bK_{ATP}K_{\gamma EC}}+\cfrac{[Gly][\gamma EC]}{aK_{Gly}K_{\gamma EC}}+\cfrac{[ATP][Gly][\gamma EC]}{abcK_{ATP}K_{Gly}K_{\gamma EC}}}}$$
ただし $${V_{max}}$$ は各酵素の最大反応速度を,$${K_x}$$ は各酵素の基質 $${x}$$ についてのミカエリス定数を,$${a, b, c}$$ は基質についての補正係数を示している.
さて上記を見ればわかる通り,反応速度式が GCL とほとんど同じである.そういうわけで今回はいきなり実験値を代入しよう.論文によれば, $${V_{max}=7.91}$$ mmol / min / mg, $${K_{\gamma EC}=0.064}$$ mM, $${K_{Gly}=0.78}$$ mM, $${K_{ATP}=0.69}$$ mM, $${a=6.68, b=0.1, c=0.29}$$ である.このとき,基質初濃度 $${[\gamma EC]_0=[Gly]_0=5}$$ mM, $${[ATP]_0=10}$$ mM, 酵素濃度 1 mg /L だったとすると GSH はどれくらいの速度で生産されるだろうか?

左が系中の化合物濃度,右が酵素反応速度の時間変化をそれぞれ示している.
その結果が Fig. 10 である.なんと約 90 秒でほぼ完全に γ-EC が GSH に変換されてしまった.Fig. 10 の反応時間の 0.3% 程度であり,GCL と GS の活性がどれほど異なるかよくわかるというものである.
GCL-GS 連続反応系の振る舞い
最後に GSH の構成アミノ酸と ATP の入った溶液に GCL, GS を入れて GSH のワンポット合成を行った場合どうなるか見てみよう.基質初濃度は先ほどと同様に $${[Gly]_0=[Cys]_0=[Gly]_0=5}$$ mM, $${[ATP]_0=10}$$ mM とし,酵素濃度も GCL, GS とも 1 mg /L だったとする.仮に両者の活性が全く同様だったとする,すなわち全ての基質について $${K_M=0.5}$$ mM で $${V_{max}=1}$$ mmol /min /mg であったとすると GSH 産生速度はどれくらいになるだろうか?
実際に算出した結果が FIg. 11 である.左端の図からわかる通り,反応開始 15 分後に約 90% まで反応が進行している.このうち γ-EC にのみ着目したものが中央の図である.GCL の基質濃度が高い反応初期は γ-EC 生産が盛んであるため蓄積していくが,反応開始から約 5 分後をピークに減少していく.これは γ-EC 濃度が高くなったことによる GS 触媒反応の速度上昇と GCL 基質減少による γ-EC 生産反応速度の低下によるものと思われる (Fig. 11 右端).

では実際の文献値に基づく値を代入した場合,各化合物の濃度推移はどうであろうか.基質濃度と酵素濃度は同様とし,ミカエリス定数と最大反応速度を文献値とした場合の結果が Fig. 12 である.左端の各化合物の濃度推移を見ればわかる通り,反応開始 250 分後でも約 75% しか反応が進行していない.γ-EC の濃度のみを取り出したものが中央の図であるが,ほぼ常にゼロであることがわかる.GCL, GS の反応速度はほぼ完全に重なり (右端),GCL が反応全体の律速段階であることが明らかである.

おわりに
というわけで,GCL と GS の反応速度の違いをなんとなく体感できた.興味深いことに,Fig. 1 のヒト細胞の GSH 濃度と同じような条件 (0.5-10 mM) における γ-EC 濃度がヒト細胞で 0.007 mM に対し今回の反応系で 0.004 mM 前後とケタの範囲で同じくらいの結果となった.Glu, Cys, Gly, ATP, $${H_2O_2}$$ の濃度を一定とし,Glutathione-peroxidase を添加した時の平衡状態を求めたりすると面白かったかもしれないが Excel で遊ぶのはこのあたりが限界という気もする.余裕ができればもう少し遊んでみたい.
