回転行列の固有値と固有ベクトルについて考えてみよう。そして行列から回転を取り出そう——行列の分解——

takubonn

2024年12月27日 08:03

回転行列とは

　みんな大好き回転行列：

$$
R=
\begin{bmatrix}
\cos\theta & -\sin\theta \\
\sin\theta & \cos\theta
\end{bmatrix}
$$

それは、ベクトルに掛けることでベクトルを角度$${θ}$$だけ回転させる、魔法のような行列。ではその固有値はどうなる？　固有ベクトルは？　行列なら固有値と固有ベクトルがあるはずだ。計算してみよう。

対象読者：
・回転行列に興味がある人
・行列は習ったが、複素数なんて出てこなかったぞ！という人
・対角化は習ったが、よく分からないまま通り過ぎてしまった人
・極分解という言葉の響きにロマンを感じてしまう人
・暇な人

回転行列の固有値eigenvalueと固有ベクトルeigenvectorを求めよう

固有値を求めよう

復習：正方行列$${A}$$の固有値$${\lambda}$$は、固有方程式$${|A-\lambda I|=0}$$で求めるのだった。

$$
|R-\lambda I|=0
\\
\begin{vmatrix}
\cos\theta -\lambda & -\sin\theta \\
\sin\theta & \cos\theta -\lambda
\end{vmatrix} =0 \\
(\cos\theta -\lambda)^2 +\sin^2\theta=0 \\
(\cos\theta -\lambda)^2 =-\sin^2\theta \\
\cos\theta -\lambda=\mp i\sin\theta \\
\lambda=\cos\theta \pm i\sin\theta \ (=\pm e^{i\theta})
$$

さて、なにやら複素数が出てきたな……。こいつの考察は後にして、先に固有ベクトルも求めてしまおう。

固有ベクトルを求めよう

復習：行列$${A}$$のそれぞれの固有値に対して固有ベクトルが考えられ、それは連立1次方程式$${(A-\lambda I)\bm x=\bm 0}$$の解（ただし1以上の自由度をもつので、特定の直線、平面、空間、…上の無数の解の集合）として得られるのだった。

$$
\lambda=\cos\theta + i\sin\theta の場合 \\
(A-\lambda I)\bm x=\bm 0 \\
\begin{bmatrix}
\cos\theta -( \cos\theta + i\sin\theta) & -\sin\theta \\
\sin\theta & \cos\theta -(\cos\theta + i\sin\theta)
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix} = \bm 0 \\
\begin{bmatrix}
-i\sin\theta & -\sin\theta \\
\sin\theta & -i\sin\theta
\end{bmatrix}
\begin{bmatrix}
x \\
y
\end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\\
$$

ここで$${\theta=0,π,2π,\dots}$$でない場合のみを考えて解く。
（※$${\theta=0,π,2π,\dots}$$ではすべてのベクトルが固有ベクトルになるが、これは回転行列が、まったく回転させない or 180°回転のときなので当然だ。面白くないので、自明なこのパターンは省く）

$$
-ix-y=0\\
y=-ix\\
x_1 =c_1\begin{bmatrix} 1 \\ -i \end{bmatrix}\\
$$

ただし$${c_1}$$は0でない任意の複素数。

同様に、

$$
\lambda=\cos\theta - i\sin\theta の場合 \\
x_2 =c_2\begin{bmatrix} 1 \\ i \end{bmatrix}\\
$$

ただし$${c_2}$$は0でない任意の複素数。

図形的意味を求めて

　実数の固有ベクトルと固有値は以下のような図形的意味をもつのだった。

行列$${A}$$の固有ベクトル：
　変換$${A}$$により「向き」が変化しないベクトル。ただし、真逆方向への変換は「向きを変えていない」と考える。要するに、変換$${A}$$により定数倍しかされないベクトルのこと。

行列$${A}$$の固有値：
　この固有値に対応する固有ベクトルが、変換$${A}$$によって引き伸ばされる倍率。

　しかし回転行列はベクトルを回転させるので、（$${θ=0,π,2π,\dots}$$の場合を除き）向きは必ず変化する。では、回転行列の複素数の固有ベクトルと固有値はいったい何を表しているんだろう。

回転行列の複素固有値

　こちらは分かる人にはすぐ分かるかもしれない。固有値$${e^{i\theta}}$$と$${e^{-i\theta}}$$は複素平面での角度$${θ,-θ}$$の回転$${\times e^{i\theta}, \times e^{-i\theta}}$$を表している。正確には$${1\cdot e^{i\theta}}$$と$${1\cdot e^{-i\theta}}$$といった感じで、「絶対値を$${1}$$倍に引き伸ばし、複素偏角に$${θ,-θ}$$を足す」変換を表している。実数のx-y平面での回転と混同しないように！　x, yがそれぞれ内なる2軸を持っていて、その2軸内での回転だ。

固有ベクトルに対する行列変換でその向きが変わらないのは定義上当たり前だが、見方を変えれば「xとyに平等に1つの固有値が掛けられるから」だと言える。複素固有値が$${Ae^{iθ}}$$のとき、固有ベクトルのxとyがそれぞれが持つ複素平面内で、平等に$${A}$$倍され、平等に偏角に$${θ}$$が足される。

回転行列の複素固有ベクトル

　実は1つ前の項が理解できたら、この項はそんなに難しくない。

説明に入る前にひとつ便利な記法を紹介する。複素数$${Ae^{iθ}}$$のことをA∠θと表すことにしよう（本当はたぶんやらないが、1∠30°を単に∠30°のようにも書いていきたい）。これは交流電気回路の分野で使う記法で、非常に直感的で分かりやすい。ここからはこれを使って書く。

　さて、本題に入ると、
回転行列の固有ベクトルの1つ目：

$$
c_1\begin{bmatrix} 1 \\ -i \end{bmatrix}
$$

（ただし$${c_1}$$は0でない任意の複素数）

が意味するのは、

・xの絶対値：yの絶対値 = 1：1
かつ
・xの偏角 - yの偏角 = 90°
であるすべての複素ベクトル$${(x,y)}$$だけは、回転行列による変換後も、その絶対値比率1：1と偏角差90°を保っている。

ということだ。例えば、
(x, y) = (1∠90°, 1∠0°)
(x, y) = (3∠110°, 3∠20°)
(x, y) = (42∠60°, 42∠-30°)
はすべて、回転行列によって絶対値比率と偏角差が変わらない（複素）ベクトルなので、回転行列に対する固有ベクトルだと言える。

複素偏角の差が90°の(x, y)なんて、実数のみの（=虚数成分が0である）x-y平面上には存在しない。これが、固有ベクトルが虚数解であることが意味するところだ。

回転行列の対角化・固有値分解

　固有値と固有ベクトルが求められたので、|対角化《diagonalization》ができる。固有ベクトルがちゃんとn本とれるn×n行列$${A}$$は、固有ベクトルを並べた行列$${P}$$によって対角行列$${D=P^{-1}AP}$$に変換できるのだった（このとき対角行列の固有値の並べ方と対応するように固有ベクトルを並べる）。$${P}$$を構成する固有ベクトルの$${c_1,c_2}$$が任意なのに大丈夫なのかと思うかもしれないが、そこは$${P}$$と$${P^{-1}}$$で上手く打ち消しあってくれるのだ（気になるなら確かめてみよう！）。また、逆に$${A=PDP^{-1}}$$のかたちで表すこともでき、これを行列の|固有値分解《eigendecomposition》という。この際、対角化の別名だと思ってもらっても、本質的には間違ってないと思う。
　回転行列$${R}$$も2×2で2つの固有ベクトルがとれるので、例に漏れず対角化/固有値分解ができる。
（※スマホだと式が見切れがちなので適宜スワイプしてください）

対角化：

$$
D_R=P^{-1}RP \\
\\
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}
=\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}^{-1}
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}\\
\\
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}=\frac{1}{2i}\begin{bmatrix} i & -1\\ i& 1 \end{bmatrix}
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}\\
\\
$$

固有値分解：（中身は省略）

$$
R=PD_R P^{-1}
\\
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
=\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}
\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}^{-1}
\\
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
=\begin{bmatrix} 1 & 1\\ -i& i \end{bmatrix}
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}
\frac{1}{2i}\begin{bmatrix} i & -1\\ i& 1 \end{bmatrix}
$$

　ここで$${P}$$の役割は基底の変換、幾何学的に言えば座標軸の変更だ。分かりやすくするために、$${c_1,c_2}$$の任意性を使って恣意的な固有ベクトルをとることで、意味が見出しやすい$${P,P^{-1}}$$を用意してみよう。

$$
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
=\frac{1}{2}\begin{bmatrix} 1 & -i\\ -i& 1 \end{bmatrix}
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}
\left(\frac{1}{2}\begin{bmatrix} 1& -i\\ -i& 1 \end{bmatrix}\right)^{-1}
\\
\begin{bmatrix} \cos θ & -\sin θ\\ \sin θ& \cos θ \end{bmatrix}
=\frac{1}{2}\begin{bmatrix} 1 & -i\\ -i& 1 \end{bmatrix}
\begin{bmatrix} ∠θ & 0\\ 0& ∠-θ \end{bmatrix}
\begin{bmatrix} 1& i\\ i& 1 \end{bmatrix}
$$

一応、上式の右辺によってベクトル$${(x,y)}$$が変換されていく様子の図解を書いた。右側の矢印から順に左へ追っていくと、それぞれの行列で何が起きるのか分かる。

　結局、回転行列の固有値分解では、「外からやってきた実ベクトル(x, y)をx-yグラフと同じ位置にプロットされる複素値に変換し、x, yの複素平面上でそれぞれθ（-θ）回転させたあと、x-yグラフに戻している」と見ることができるだけだった。面白みがない。x平面上の変換とy平面上の変換は対称なので、固有値の∠θ、∠-θというダブった情報は2つで1つしかおしごとをしていないと言える。虚数あるあるだ。

︙

🧨ここで終わったら面白くないだろ💥

行列から回転を取り出せ！

　回転行列を固有値分解してもつまらない結果が得られただけだったけど、今度は普通の行列に含まれる回転成分がどのようになっているか気になってきた。
　というわけで、例として適当な計算しやすいように選んだおためし行列を持ってきたからこれで遊ぼう。

$$
\begin{bmatrix} 1 & -1\\ 2& 3\end{bmatrix}
$$

固有値分解eigendecompositionと相似変換similarity transformationで回転を取り出す（？）

　まずは、回転を含む一般の2×2行列で計算してみたい。

$$
A=\begin{bmatrix} a& b\\ c& d\end{bmatrix}
$$

を固有値分解してみる。
…………LaTeXで書くの疲れたから手書きにするぞ！　これA=\begin{bmatrix} 1 & -1 \\ 2& 3\end{bmatrix}みたいなことイチイチ書いてコンパイル綺麗な数式に変換させてるんだぜ！やってられるか！！

固有値分解ができたら、前の章で書いた対角化された回転行列を代入する。ありがたいことに、虚数成分が上手く打ち消しあって、実行列だけが残る。

　というわけで、回転を含む行列は、「（定数倍）-拡大縮小-せん断※-回転-せん断-拡大縮小」の組み合わせで表せることが分かった。

※せん断（シアーshear）とは、物体を横ずらしさせるように力が作用すること。簡単に言えば、底辺の長さと高さを変えずに長方形を平行四辺形に変形させる作用。

　このように、行列$${A}$$をある行列$${Q}$$によって固有値が等しい別の行列$${B=Q^{-1}AQ}$$で表すことを、行列の相似変換similarity transformationという。また$${A}$$と$${B}$$は相似similarであるという。

実際におためし行列を代入して、変換を追ってみよう。

なんか偶然「拡大縮小」の部分が何もしない単位行列になってしまったが、お試し行列$${A}$$は「x方向1倍せん断→約26.6°回転→x方向-1倍せん断→√5倍する」に分解できることが分かった。
（x方向1倍せん断なんて言葉は今作った）

図は、ベクトル$${(1,0),(0,1)}$$で作られる1×1の正方形（黒）が、せん断（赤）、回転（オレンジ）、逆せん断（緑）、定数倍（青）と変換されていく様子。

お〜！！

　ただ、目的であった「回転を取り出す」ことに関しては微妙だ。作用として切り分けることはできたが、回転行列が行列の積の左端または右端に露出していない。「この行列が純粋な回転に見える世界」に持っていき、回転させ、また元の世界に持ってくる、という操作をしている。元の世界から見た回転の描像は、この回転行列とは異なっているだろう（楕円状かな）。面白い結果ではあるが、別のアプローチを探したい。

極分解polar decompositionで回転を取り出そう

（※説明が難しいと感じる部分があれば適当に読み飛ばして進んでください）

　これはさっきの相似変換とは本質が違うことを断っておく。相似変換のほうは基底変換以外の部分を「回転（複素固有値）」または「反転を含む拡大縮小（実固有値）と捉えていたのに対し、こちらは基底の非直交的な成分が回転に、負の固有値が反転に現れる。つまり、固有ベクトルが直交しない変換はすべて回転を持つと考える。

　さて、任意の行列$${A}$$はユニタリー行列$${U}$$と正定値エルミート行列$${P}$$で$${A=UP}$$と表せる……らしい。さらに$${A}$$が正則であればこの分解は一意に定まるらしい。一意に定めるために（半）正定値と規定していると言ってもよいだろう。「反転（=負の固有値）」という要素を対称行列$${P}$$側ではなく直交行列$${U}$$側に押しつけることで、直交行列はただの回転行列ではなく回転行列に反転行列が掛けられているものになるかもしれないが、いずれにせよ直交行列ではある。

※複素数の行列では普通、転置の代わりに「エルミート転置」を使う。これは転置をとってさらに全要素に共役をとるもので、$${A}$$のエルミート転置を$${A^{†}}$$と表す。~~†中二病†~~

※ユニタリー行列は$${U^{†}U=UU^{†}=I}$$（$${I}$$は単位行列）を満たす行列$${U}$$。実行列だと直交行列。

※エルミート行列は$${A^{†}=A}$$を満たす行列$${A}$$。実行列だと対称行列。

※正定値行列とは、固有値がすべて正の実数である行列。

要するに、極分解は実行列の範囲で見れば、任意の変換を「拡大縮小を持たない、純粋な回転と反転の積$${U}$$」と「回転や反転を持たない、純粋な直交方向への拡大縮小$${P}$$」に分解するものだといえる。

行列$${P,U}$$は対角化によって行列の平方根を使って求めることができる。
（英語版Wikipedia - Polar decomposition などを参照。https://en.m.wikipedia.org/wiki/Polar_decomposition）

しかし、今回は2×2行列について考えるので、また、$${A}$$が実行列→$${P,U}$$も実行列なので、より簡単な方程式を立てて$${P,U}$$を求める。証明は少しだけ長いので結論部分だけ載せる。
（証明は付録に置いておくので、気になる人は追ってみてください）

実際におためし行列を代入してみる。

ベクトル$${(1,0),(0,1)}$$で作られる1×1の正方形を考え、それが$${P}$$によって平行四辺形（赤）になり、さらに$${U}$$によって反転・回転されて平行四辺形（オレンジ）になる様子を図で見てみよう。
緑と青の直線は$${P}$$の固有ベクトルの方向を表している。確かに直交している（非回転的）。

　固有値が実数である行列も代入してみよう。こういうのはだいたい、いろいろなパターンを試すことで見えてくるものだ。

＜試したパターン＞
（A: 固有値が共役な複素数（⇔行列式は正））
B: 固有値が2つとも負（⇔行列式は正）
F: 固有値が正と負（⇔行列式は負）
G: 固有値が2重解（⇔行列式は正）
H: 固有値の1つが0（⇔行列式は0）

※行列式が負であれば反転を持つことになる。まだ、n次正方行列の行列式はn個の固有値の積（証明は各自調べて）。よって、今回のように2次正方行列の場合、Aのような固有値が共役複素数パターンでは行列式は必ず正で、反転を持たない。

この式成り立つのキモいな。正定値じゃない対称行列は、ちゃんと正定値の対称行列に分解されるんだね。

図では分かりにくいが、行列Fによって、(1, 0)はオレンジの平行四辺形の傾きのキツい辺に、(0, 1)は傾きのユルい辺に変換される；つまり裏返ることになる。
オレンジと赤が互いに、裏返しにしないと重ならないことを確認してほしい。

重解だからといって特別なことが起きるわけではないようだ。強いて言うなら、行列式が必ず正になるので、反転はない。

行列式が0、つまりHは正則でないので、2通りの極分解が存在する。Pは共通している。

Pは、Hの固有値0の固有ベクトルとまったく同じ方向の、固有値0の固有ベクトルを持つ。
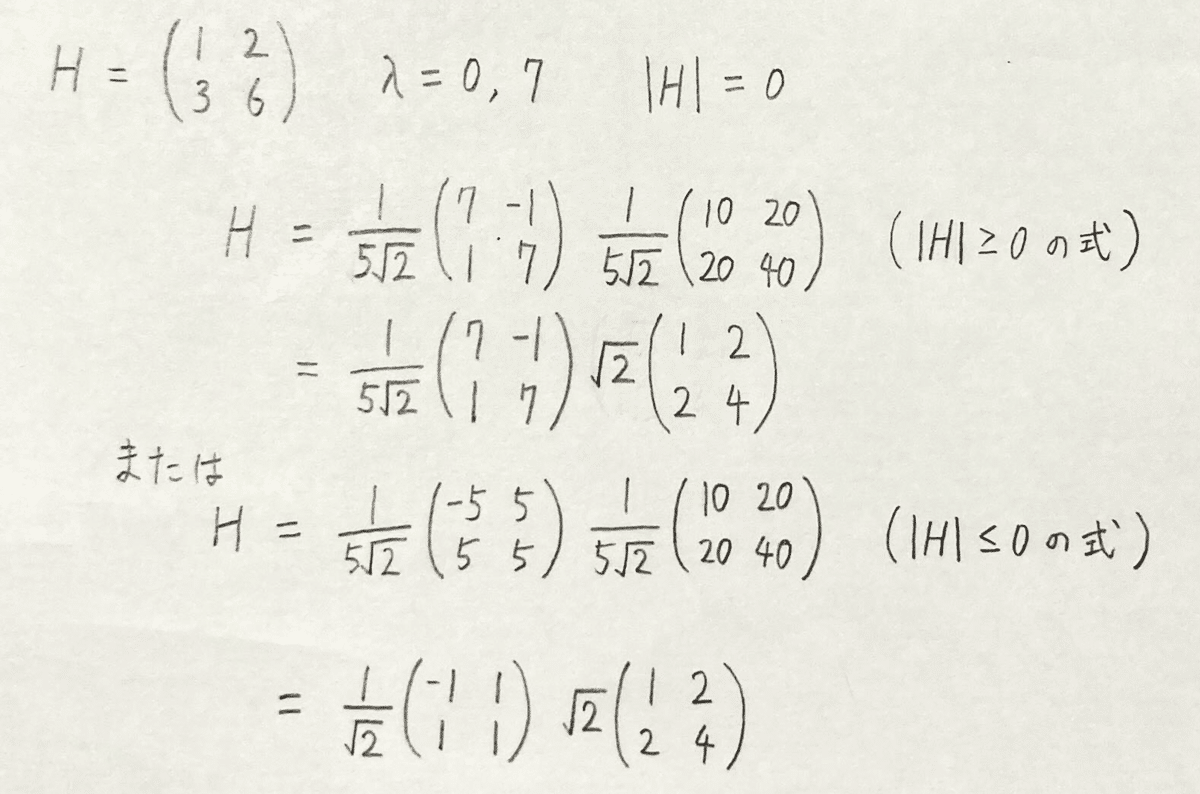
固有値0により、対応する緑の固有ベクトル方向の成分はなくなり、青の固有ベクトル上に潰れる。
直線になるので「表裏」がなくなり、「回転+反転」が「別の回転」と等価になってしまうことで、2通りで表せるわけだ。

　拡大縮小と回転に綺麗に分解できて気持ちいいではないか！！　ある変換が直交する伸び縮みと回転に分けられる（反転を伸び縮み側に含めるか回転側に含めるかはさておき）のは幾何学的直観にもよく適合する。まるベクトル解析の発散$${\mathrm{div}}$$と回転$${\mathrm{rot}}$$のようだね。

　軸を傾けることを非回転と捉える立場（固有値分解）と、固有ベクトルが直交する変換が非回転だと捉える立場（極分解）で、こんなにも姿が違うのは面白い。どちらがより気持ちいいと感じるかはあなた次第。

何はともあれこれにて解決！

おまけ——ちくわの中身深淵のぞき

　今回この記事を書いている途中に面白いことに気づいてしまった。実は昔から気になっていたことがある。

「なぜ2次元から3次元になっても『3次元すごい回転』が生まれたりせず、ある軸に垂直な2次元平面で回転するだけなのか」

3次元における回転は貧相なのだ。「3次元の回転行列」を初めて見たときの拍子抜け間は異常だった。

今回この謎がやっと解けた。

　3次元における線形変換は、あるステップで$${x,y,z}$$の位置にあるものが、その位置に依存して次のステップで$${x',y',z'}$$の位置に移ることに、対応させられる。そして、固有値分解において、回転は複素数の固有値で表されるのだった。

$${x'=ax+by+cz}$$のようにつく係数はすべて実数だ。実3次元空間を実3次元空間に対応させるのだから当たり前だ。だから係数$${a,b,c,d,e,f,g,h,i}$$による3次正方行列の固有値は、実係数3次固有方程式の解となる。

実係数の方程式の解は、必ず実軸に対称に現れる。なぜなら、$${βz+γz^2+…=α}$$で$${z=A∠θ}$$を解として代入した左辺が実軸上の$${α}$$にのるなら、大きさが同じで逆回転の$${z=A∠-θ}$$もまた実軸上の$${α}$$にのるはずだからだ。
そしてn次方程式は、重解含め、必ずn個の解を持つので、3次方程式も複素平面上に3つの解を持つ。

よって、3次方程式が持てる虚数解の数は0個か2個。言い換えれば、最低1つは実数解であり、回転に関わることができない。3つが虚数解の「すごい回転」は存在できないのだ。

じゃあ4次元なら……

できます！！　やったね！　共役なペアが2つ作れるから、2平面での回転の合成ではあるけれどできちゃうぞ！

付録（2×2極分解の明示形式）

　2×2行列の成分$${a,b,c,d}$$によって$${A=PU}$$が一意に表せることの証明。