【高等学校 Rを使ったデータ分析 no.5】授業に向けての一歩
「探究活動」として、「情報I」として授業を行う場合、どこからスタートしたら良いか、そんな不安に対し、早稲田大学「高校生のためのRによる回帰分析」(2024/11/13アクセス)を参考にしてみました。
今回は、このスライドの流れに沿ってRStudioを利用してみました。前提と
しては数学Iの履修は必要かなと思います。
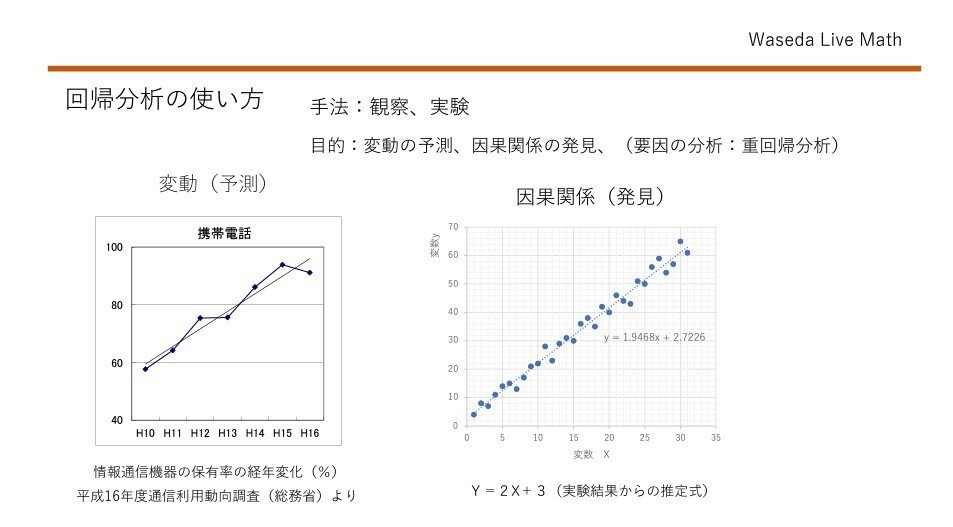
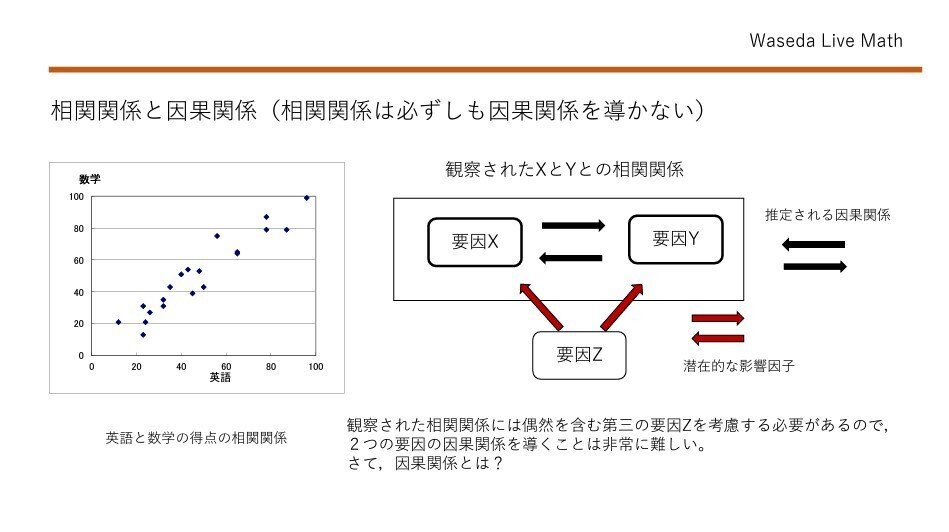
まずは、スライド2ページ

最新のデータを政府統計の総合窓口(以降e-Stat)より用意しました。e-Statから時系列表をたどると統計Dashboardに移動します。必要なデータをExcalでまとめます。
# 手順1 Excelファイルの読み込み
> install.packages('readxl') # Excelファイルの読み込み準備
> library(readxl)
> pop <- read_excel("pop.xlsx", skip=1,range = "A2:B83") # 2行目以降のA列(調査年year)とB列(総人口number)を読み込み
> pop
# A tibble: 81 × 2
year number
<dbl> <dbl>
1 1920 55963053
2 1925 59736822
3 1930 64450005
4 1935 69254148
5 1940 73075071
6 1945 71998104
7 1950 84114574
8 1951 84541000
9 1952 85808000
10 1953 86981000
# i 71 more rows
# i Use `print(n = ...)` to see more rows# 手順2 pop.lmを定義
> pop.lm <- lm(number~year, data=pop) # lm(目的変数~説明変数,data=データ名)# 手順3 回帰直線を描く
> plot(pop) # 散布図の描画
> abline(pop.lm, lwd=2) # 回帰直線の追加 lmwは線の太さ
# 図2 参照
>
> coefficients(pop.lm) # 回帰直線の切片と傾き
(Intercept) year
-1275762514.9 699386.4
> cor(pop$year, pop$number) # 相関係数
[1] 0.9374342
>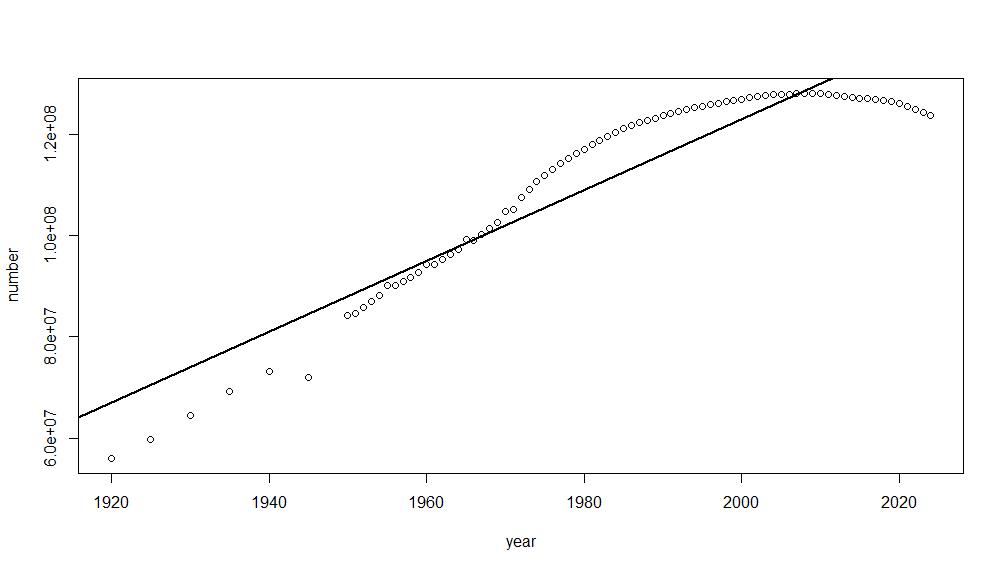
# 手順4 要約
> summary(pop.lm) # lmの要約
Call:
lm(formula = number ~ year, data = pop)
Residuals:
Min 1Q Median 3Q Max
-16005595 -3809958 265431 6056858 8529399
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.276e+09 5.796e+07 -22.01 <2e-16 ***
year 6.994e+05 2.922e+04 23.93 <2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 6670000 on 79 degrees of freedom
Multiple R-squared: 0.8788, Adjusted R-squared: 0.8772
F-statistic: 572.7 on 1 and 79 DF, p-value: < 2.2e-16# 回帰分析
> pre <- predict(pop.lm) # 予測値(回帰で計算される値)
> res <- residuals(pop.lm) # 残差(実データ値 - 予測値)
> data.frame(pop, pre, res)
year number pre res
1 1920 55963053 67059407 -11096354.2
2 1925 59736822 70556339 -10819517.2
3 1930 64450005 74053271 -9603266.3
4 1935 69254148 77550203 -8296055.4
5 1940 73075071 81047136 -7972064.5
6 1945 71998104 84544068 -12545963.6
7 1950 84114574 88041000 -3926425.7
8 1951 84541000 88740386 -4199386.1
9 1952 85808000 89439773 -3631772.5
10 1953 86981000 90139159 -3158158.9
11 1954 88239000 90838545 -2599545.4
12 1955 90076594 91537932 -1461337.8
13 1956 90172000 92237318 -2065318.2
14 1957 90928000 92936705 -2008704.6
15 1958 91767000 93636091 -1869091.0
16 1959 92641000 94335477 -1694477.4
…..
> スライドでは、「この結果からどのようなデータ分析が可能か考えよ。」となっています。
最後に、「情報I」ではスライドの8,9ページにある以下が重要です。一連の分析手法をメインにするのではなく、出てきた数字に対して考察する時間を大切にしたいと思います。