長乗法・短乗法、長除法・短除法

　筆算の計算をめんどくさくする操作の１つがくり上がり・くり下がりの操作です。「筆算研究室」のnoteでは，くり上がり・くり下がりをまとめて桁またぎと名づけていますが，この桁またぎをかけ算・わり算の筆算のときにどのように書いて処理するか、考え方が２つあります。

　長乗法／短乗法、長除法／短除法です。

　長除法・短除法については啓林館の教員向け解説ページに説明があるので，引用します。

長除法・短除法｜算数用語集

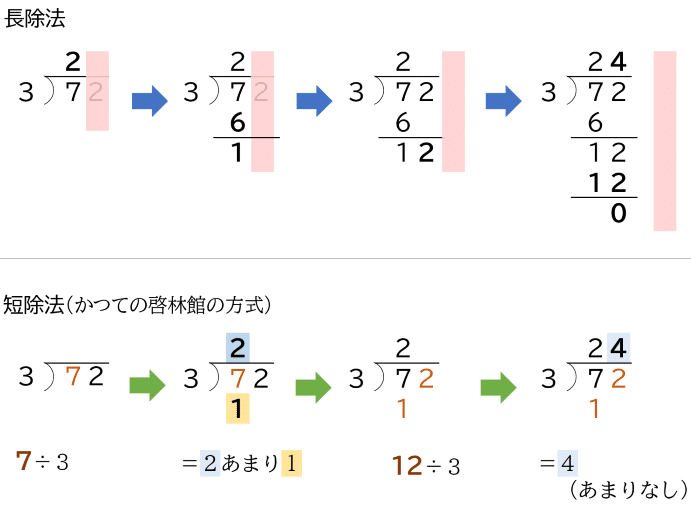
　わり算の筆算で，上のように，商の位ごとに商と除数の積，途中の余りなどを順次かいて計算を進めていく方法を，長除法といいます。
　これに対して，右のように，部分積をかかずに途中の計算過程を暗算で行いながら計算を進めていく方法を，短除法といいます。
　長除法，短除法のいずれも，頭の位から順次「たてる」「かける」「ひく」「おろす」という操作をしていく計算の手順に変わりはありません。違いは，部分積をかくかかかないかです。
　わり算の指導では，「たてる」「かける」「ひく」「おろす」という筆算のアルゴリズムを，視覚的に捉えやすい長除法でしっかりおさえることが大切です。
　短除法はその発展として挑戦させたい内容であって，全員に徹底をはかる必要はありません。
　教科書では，こうした趣旨から，短除法は取り上げていませんが，興味・関心に応じて発展的に扱うことは可能です。
　なお，かけ算の筆算においては，かける数が１桁のとき，計算を簡略化するため，長乗法でなく，途中の部分積をかかずに念頭で処理する短乗法を指導しています。

　しれっと「「たてる」「かける」「ひく」「おろす」という筆算のアルゴリズムを，視覚的に捉えやすい長除法でしっかりおさえることが大切です」と書いてありますが、かつて啓林館は÷１桁を短除法で指導し、水道方式側がそれを批判するという構造だったのです（『多位数の除法　算数わかる教え方学び方１１　後藤田明孝　国土社』）。それが「短除法は取り上げていませんが，興味・関心に応じて発展的に扱うことは可能」という表現に歴史的な流れがあらわれているということもできます。

　水道方式（遠山？）が÷１桁は短除法、÷複数桁が長除法で筆算させること（戦前の緑表紙？啓林館？）を批判していた文章をどっかで読んだような気もするのですが、今いろいろ探しても出てきませんでした。とにかく÷１桁も÷２桁も同じわり算の形で書ける方がよいこと、「たてる→かける→ひく→おろす」のアルゴリズムを合わせること、暗算を極力排すること・・・を優先したことなのではないか、と思う。（そうでなければ、かけ算を短除法で計算させることと帳尻が合わない！）

　公文式が（÷複数桁でも）短除法だったりもするのですが、とにもかくにも、教える側が「筆算はこれしかない！」とならず、いろいろな方法を知っていて，その子の段階に合わせて提示できればそれでいいのではないか、と思うのですが・・・　ぜいたくかしら・・・

　個人的には、÷１桁の短除法は「知る人ぞ知る」の技にしておいてはいけなくて、今後の約分・通分でも、素因数分解でも、÷１桁はできるだけ速く解ける方法は身につけた方がよいと思っていて、÷２桁以降は長除法＋電卓活用で深追いしなくてよいような気がしています。（とはいいながら，かなり問題分類や難度分析やアルゴリズムや体系性ににこだわってはいますが）

　ちなみに、乗法についても、×１桁で短乗法が難しいようなら、紙もエンピツもケチらず長乗法でやってしまった方が、中途半端に暗算して計算ミスせず済むのにな，と思っています