行動経済学　用語集　損失回避性　(プロスペクト理論関連)

プロスペクト理論関連

Δｘを、参照点（reference point）からの厚生(welfare)変化とする

価値関数　V(Δｘ,p)＝v(Δｘ）w(p)

厚生変化Δｘが生じる

確率をpとする。

w(p)は確率ウェイト関数

損失回避：　

プロスペクト理論の価値関数v(Δｘ)について、

v’ (for Δｘ＞0) < v’ ( for Δｘ<0)　

が成立するということを指し示す用語。v’ ( for Δｘ<0)　＞0　であることに留意すること。

（’はΔｘでの微分）

損失においては、リスクが好まれる（確実な損失よりも、不確実な損失が好まれる）：

危険回避度について

 -v’’/v’ <0 for Δｘ＜0 

が成立するということを指し示す用語。

（入門的レベルでは確率ウェイト関数w(p)の影響は考慮せずに

論じられる
参考：心理物理学的に、確率ウェイト関数（確率加重関数）の関数形を導出した研究論文はこちらのリンク (PDFはこちら) ）

利得に関しては、リスクが回避される：

危険回避度について

 -v’’/v’ >0 for Δｘ>0

が成立すること。

（入門的レベルでは確率ウェイト関数w(p)の影響は考慮せずに

論じられる）

感応度逓減(逓増）：

ｖ’’の符号が負（正）であること。プロスペクト理論においては、Δｘ＜0ではこの符号が正(感応度逓増）、Δｘ＞0では負（感応度逓減）である。

損失回避とリスク回避の関係

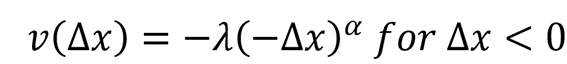
とプロスペクト理論の価値関数を特定化した場合、
損失回避係数λ>1(普通はλが1より大きいことをloss aversion「損失回避」と
呼ぶ)が、危険（リスク）回避度（二階微分と一階微分の比に負符号をつけたもの）に影響しないことは以下のように示せる。

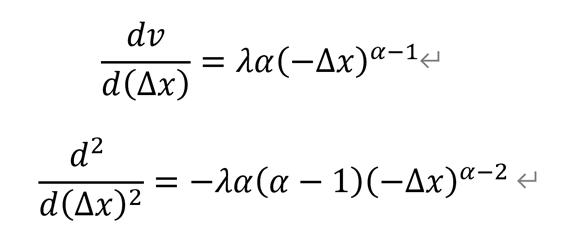
したがって、（確率ウェイト関数の影響を考慮しない）危険回避度は、

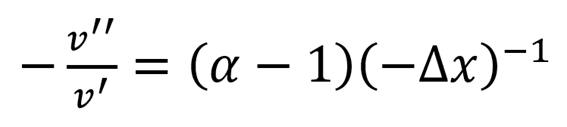
となり危険回避度というパラメータの大きさや正負に、損失回避λが影響を
与えないということがわかる。ふつうは0＜α＜1なので、Δｘ＜0（損失フレーム）では危険回避度が負、すなわち、「損失領域ではリスクが好まれる（絶対確実な損よりも、不確実な損のほうが受け入れられやすい）」ことが、プロスペクト理論の価値関数の（数学的な意味としては）形状を決定するパラメータα（心理学的には、感応度逓減性diminishing sensitivityに関連するパラメータ）から（損失回避傾向の強さ＝λ　とは無関係に）結論される。

プロスペクト理論の経済学からみた発展史の論文解説の講義資料へのリンク。