行動経済学　用語集（時間選好　ナッジ　関連）

参考１：神経経済学Neuroeconomicsにおける時間選好time preferenceや異時点間選択intertemporal choiceに興味がある場合はこのリンクを参照のこと。PDFはここ

参考２：心理物理学的に双曲割引を導出した研究論文はこちら (PDFはここ）日本語解説はこちら

時間選好関連
(連続時間において、各時点の関数として説明）

割引効用モデル（Discounted utility model）

時点ｔにおける消費c_tから得られる効用U（大文字）が以下のように、時点によらず消費量だけで決まる効用u（小文字）とそれ以外の、その消費がその時点ｔであることの影響（時間割引関数）との積に分解できると仮定している。

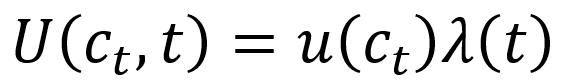
※　均衡の時間選好率≠時間割引率≠時間割引関数

であるため、各種用語に対応する数式を正確に区別することが、この分野のデータ解析において重要なので、はじめにこの点を記す。

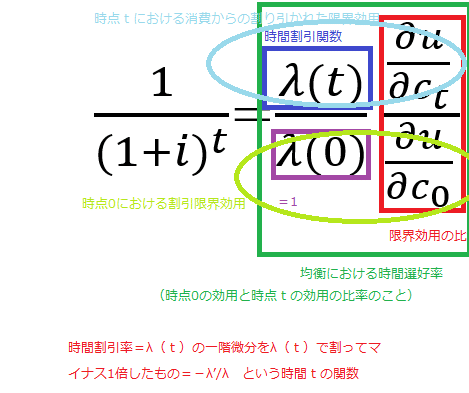
均衡における時間選好率(time preference)：

均衡においては、時間を通じて変化しない市場利子率iについて、以下の関係式が成立する。

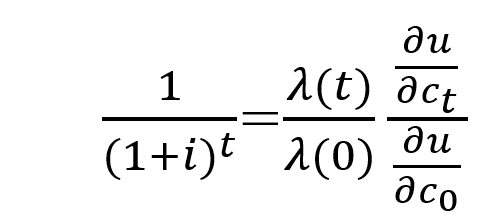
この右辺は異時点間の消費の限界代替率（marginal rate of substitution)　である。この「異時点間・限界代替率」は2時点における時間割引関数の割引率たちの比　と　2時点における消費から得られる「時間割引された限界効用」たちの比（時間割引されていない2時点の限界効用の比と2時点の時間割引関数の比の積）である。

ナッジを考える場合の時間選好率：

上記の、均衡における時間選好率は2つの理論変数たちの比の積であるが、このうち前者の分子λ（ｔ）を時間割引関数と定義し、

-λ'/λ　をその1時点の時間割引率

と定義する。一般には、これはtの関数である。すなわち、上記の市場利子率i　のように、時間を通じて変化しないという意味の定数であるとは限らない。またλ（0）＝1である。

（ただし、標準的なファイナンス理論においても、市場金利iについても、「金利の期間構造」を想定する場合ある）

このように、ここでの用法によると、

均衡の時間選好率（異時点間限界代替率）を限界効用の比で除したもの

＝時間割引関数 (time-discount function)

≠時間割引率 (time-discount rate)　

＝ナッジについて考える場合の時間選好（time preference）率　

である。（リチャード・セイラーの1981年の論文 Some empirical evidence on dynamic inconsistencyで分析されているのもこれら最後の2つの変数である）

-------------------------------------------------------------------------------

以下に、行動データの分析を行う際に標準的である、効用Uを用いた定義・説明を記す。

時間割引率（time-discount rate）：

　-[dU(c,t)/dt]/U(c,t)
（U(c,t)は時点tにおいて、消費ｃ>0から得られる効用、割引効用discounted utilityと呼ばれるもの

時間割引(time discounting, delay discounting遅延割引とも似た概念)：

U(c, t1)>U(c, t2) if t2>t1　
が成立することを、時点t1（早い時点）と時点t2（遅い時点）の間で時間割引が起こっている、という。
(この2点が一致する極限では、dU/dt<0 if |t1-t2|→0　のことである)

現在バイアス(present bias):　

-[dU(c,t)/dt]/U(c,t) がt>0でt=0より小さいこと
-[dU(c,t=0)/dt]/U(c,t=0) > -[dU(c,t>0)/dt]/U(c,t>0) 

時間非整合性(Strotz,1955 )　（time inconsistency)：

動的非整合性（dynamic inconsistency）とも呼ばれる。
生涯効用（消費経路C(t)の汎関数）の最大化問題

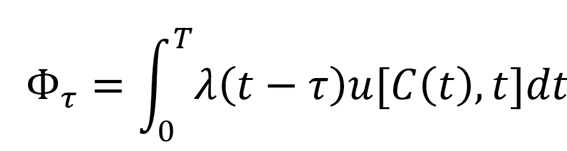
ただし、
λを時間割引関数、Tは終端時点、C(t)は時点ｔにおける消費、uはその消費によって受けるその時点における効用（utility)、τは０＜τ＜Tを満たす任意の実数（計画をたてる日：ｔ＝0　からの経過時間）である、を考える。

この場合にτをある一定値（たとえばτ＝0）に固定して、（λが指数関数でない場合は、τの変化の影響も考慮しなくてはいけないのに考慮せず）、「素朴に」一時点におけるオイラー方程式

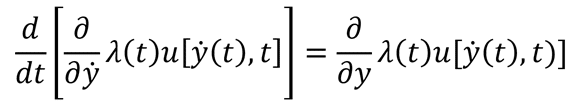
の解C(t)をその時点以降の最適消費経路とする「計画」を立ててしまうこと（このように、一時点の事情のみを考慮して将来計画をたててしまうことを、近視眼性myopiaとよぶ）によって、最適消費経路が、計画策定時点からの経過時間の長さτごとに異なる経路となってしまうこと。ただし、C(t)=yの時間微分（yの上にドットを打ったもの）。λが時間の指数関数である場合には（またその場合に限って）、このような「近視眼的」な決定を行っても、時間非整合性は生じない（ノーベル経済学賞受賞者のPhelpsが証明した）。このように、時間割引率が大きいからと言って、「近視眼的」な時間非整合性が生じるわけではないので、近視眼的な意思決定者（経済主体）が非合理的である（このことは、非指数関数割引の場合は正しい）からといって時間割引率の大きい経済主体まで非合理的なのだろう、と誤解しないことが、理論モデルや行動データの解釈のために重要である。

[原論文] Myopia and Inconsistency in Dynamic Utility Maximization
R. H. Strotz Review of Economic Studies, 1955, vol. 23, issue 3, 165-180

選好の逆転(preference reversal)：

参考：youtube動画による解説はこちら

U(c1,　t1)>U(c2,　t2) が成立する
（ｃ１＞ｃ２、ｔ１＞ｔ２と仮定、つまりより遅く消費される大きな報酬を、より早く消費される小さな報酬よりも好む）
にも関わらず、この不等式が成立した時点からτなる時間の長さが経過すると
U(c1,　t1－τ）＜　U(c2, t2-τ）
と不等号の向きが逆転して、小さいけれども早く消費できる報酬のほうが好まれるようになってしまうこと。

逓減的性急度（decreasing impatience）:

選好の逆転がおこるまでの時間間隔τの短さのこと。

(流動的な計画＝Strotzの意味で近視眼的な予定の「流動性」の強さ、これがつよいほど素早く予定が変更されてしまうという時間非整合性の強度を表す量である）

-[logλ]''/[logλ]'によって定義できることが、以下の論文で数学的に証明された：

Decreasing Impatience: A Criterion for Non-Stationary Time Preference and “Hyperbolic” Discounting
October 2004Scandinavian Journal of Economics 106(3):511-532
Drazen Prelec

・小さくてもよいからなるべく早く消費できる報酬への選好（impatience）＝時間割引率＝　-λ’/λ　とは異なる量である。

時間非整合性：Prelec逓減的性急度 (高橋泰城note記事まとめ）｜高橋泰城（たかはしたいき）

・代表的な時間割引関数に対するDI（decreasing impatience）の関数形はこのリンクを参照のこと。

符号効果（sign effect）：　

｜-[dU-(-c,t)/dt]/U-(-c,t)｜　＜　-[dU+(c,t)/dt]/U+(c,t)　
U+は報酬の効用、U-は損失の効用

いやなことを予定より先延ばし（procrastination）すること:

if t2 >t1（>0）then　
｜-[dU-(-c,t)/dt]/U-(-c,t)| for t1 > ｜-[dU-(-c,t)/dt]/U-(-c,t)| for t2

(ここでは、行動経済学における概念を統一的に把握するために、レモン市場の研究などでノーベル経済学賞を受賞したAkerlofによって、以下の論文に用いられた、時間整合性を欠いた先延ばしのことをprocrastinationと定義している。時間整合的に損失を強く割り引くことは、Strotz1955の意味での「近視眼性」を引き起こさないからである。）

Procrastination and obedience
GA Akerlof - The American Economic Review, 1991

”In this lecture I shall focus on situations involving repeated decisions with time inconsistent behavior.”

2024年に、実生活における先延ばしが時間割引で予測できるという報告がありました：
Temporal discounting predicts procrastination in the real world | Scientific Reports (nature.com)

時間選好におけるナッジ

Strotz1955が考察したような「時間非整合性」は、たとえば時間割引関数が指数関数でない場合に生じ、計画策定時点からの経過時間τによって最適消費計画が異なる（Thaler 1981によって人間においてもこのようなことが起こっていることが示された　Economics Letters
Volume 8, Issue 3, 1981, Pages 201-207）。多くの場合、計画策定時点からの経過時間τ（報酬までの待ち時間ではない）が小さいほど、時間割引率が小さい消費計画となっている（双曲割引hyperbolic discountingとよばれる現象）。このような場合には、計画策定者本人にとっても、どのτに対応する将来計画が自分のやりたいことなのかが「ただ一通りには」定義不可能になる。すなわち、（時間割引関数が指数関数でない）ある同一人物において、
optimal C(t) for τ1　≠　optimal C(t) for τ2　if 　τ1　≠　τ2
という時間非整合性が生じてしまう。
そこでThalerらは、なるべくτが小さい時点のその人の将来計画を(ほかの人がデフォルトルールなどに設定しておいてあげて）本人が（そのあと時間の経過とともにτが大きくなっても、すなわち時間割引率が大きくなっても）計画変更をしにくいようにしておけば、当初の予定（τ＝0における最適消費計画）通りの消費経路をたどることができるので、（τ＝0における本人にとって）望ましいのではないかと提案した（年金制度などの工夫）。これが（時間選好における）ナッジ（nudge)の一例である。

[ もともとのStrotz, 1955の指摘]:
” The　individual over time is an infinity of individuals, and the familiar problems of interpersonal　utility comparisons are there to plague us." Strotz,1955 Rev Econ Stud.
(割引関数の形状が指数関数でない意思決定者の動的決定問題においては時間軸上の「個人」が無限人数より構成されることになってしまうので、個人間の効用比較可能性問題という、厚生経済学のお馴染みの問題が生じてしまう　こと、それ（＝消費者の時間選好が一通りに定まらないということ）によって、ピグー流厚生経済学の観点からは、政府の介入が正当化されるという可能性が指摘されている。）

Thaler, Richard,　"Some empirical evidence on dynamic inconsistency"
Economics Letters Volume 8, Issue 3, 1981, Pages 201-207

↓に関連する行動実験の資料（自分の時間割引率が測定可能）がある。

ナッジの定義:
経済学からはインセンティブとみなせない方法で（予測できる）任意の(any)行動変容のアーキテクチャーのこと
（リチャード・セイラーら "any aspect of the choice architecture that alters people's behavior in a predictable way without forbidding any options or significantly changing their economic incentives" https://pubmed.ncbi.nlm.nih.gov/29590519/ ）
金銭的インセンティブではないインセンティブ（非金銭的インセンティブ）によって人を行動変容させることも、経済学的にはインセンティブによる行動変容に含まれるのでナッジではないことに注意すること