
行動計量学 講義資料(高橋泰城 たかはし たいき 2023後期)
(講義は水曜4限、W202)
講義のねらい
心理学や行動経済学を学んだのち、大学院進学などを経て研究生活を送る人の役に立つだけでなく、情報処理技術者試験などによる資格をとって、ITコンサルタント、データサイエンティスト、AI開発、ソフトウェアやネットワークエンジニアになるという人も結構いるので、情報処理技術者試験や統計学検定、データサイエンス数学ストラテジスト試験、アクチュアリー試験の対策にもなるような情報・解説もときおり挿入しますのでご参考にしてください。
この講義ではRという統計分析用の言語および実行環境を用います。Rは統計解析や機械学習の分野に適しています。データ分析やグラフ描画などの多数のソフトウェアパッケージが提供されています。Rにおいて用いられる変数には「型」を指定する必要がなく、実行時に変数に代入されるオブジェクトの型が決定されます(動的型付け言語とよばれるものの一種です)。
また、Rに入門する際には、入力するテキストや数字の文字コードに注意することが必要ですので、そのあたりの知識が不足している人は、こちらを一読してください。
R入門者のための文字コード入門|高橋泰城 (note.com)
以下の資料のテキストファイルはWindowsで作成したので、MacOS上で開く際には、何かエラーや想定外の挙動を示す場合があります。その際には、Macのfinderから「テキストエディット」というMacアプリを起動し、そのアプリから拡張子が.txtのテキストファイルを開いてみてください。
※レポートの提出はメール添付ファイルで
2023Rreport@gmail.com
に送信してください。
参考1 レポート提出用に、自分のコンピュータ画面のスクリーンショット(スクショ)を取りたいときは、Windowsでは、Windows ロゴ キーを押しながら Shift キーを押しながら S キーを押します。(またはFnキーとPrint Screenキーを同時に押す)。Macでは「shift」「command」「3」の 3 つのキーを同時に長押しします。
参考2 統計学の高校から大学1年前期レベルのテキストは
初学レベル向け(統計学一般) | 書籍紹介 | 統計WEB (bellcurve.jp)
を参考に選んでください。大学1年次後半レベルは
基礎レベル向け(統計学一般) | 書籍紹介 | 統計WEB (bellcurve.jp)
にあります。大学2年次-3年次レベルは
中級レベル向け(統計学一般) | 書籍紹介 | 統計WEB (bellcurve.jp)
にあるテキストから選んでみるのがよいでしょう。
参考3 レポートを作成する際には
統計学の時間 | 統計WEB (bellcurve.jp)
の統計学コースの各項目も参照するとよいでしょう。
講義1回目
Rでどんなことができるかのデモンストレーションです。はじめのうちはあまり数式などはでてこないような例で話をすすめていきます。でも、数学的背景も知りたいし、自分で数式の計算もできるようになりたいという受講生は、たとえば経済学で使われる数学の入門的資料へのリンク(ミクロ経済学で用いられる数学 講義資料 偏微分、テイラー展開、キューン・タッカー条件、凹関数 準凹関数、 ラグランジュ未定乗数法 固有値 固有ベクトル など 高橋泰城 (たかはし たいき)担当 2021|高橋泰城 (note.com))を適宜参照してください。
ちなみに、Rの利点の一つは、比較的簡単にいろいろなグラフが描画できることです。科学研究において、グラフを用いたコミュニケーションがなぜ大切なのか?という理由については、こちらのリンクをご参照ください。
グラフ占有率(FGA):研究分野の立ち位置の指標の一つ|高橋泰城 (note.com)
デモンストレーション
コイン投げにかかる時間の計測

#次にポリゴンでデザインを描いてみましょう
#3次元のオブジェクトを描いてみましょう
#三角関数を描いてみようsin(x)
#散弾銃の弾丸の痕を描いてみよう
#散弾銃の弾丸の箱ひげ図
講義2回目
2回目講義用のデモンストレーション---その1 音のフーリエ変換 波形を見て確認しよう
まず、以下のようにして440Hzの正弦波の音を出してみましょう。
>install.packages(tuneR) #まずtuneRのパッケージを外部からインストール
> library(tuneR)
> beep <- sine(440)
> play(beep)
(Macの方は
tuneR::setWavplayer('/usr/bin/afplay')
beep=sine(440)
play(beep)
としてみてください)
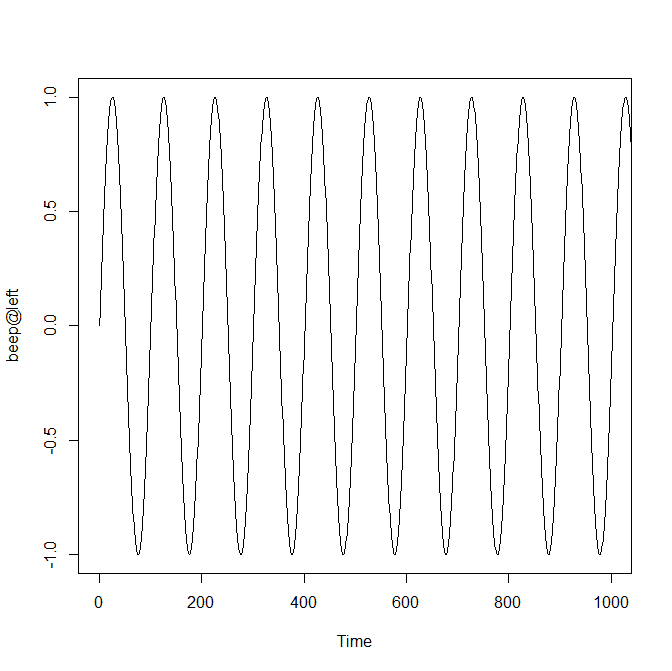
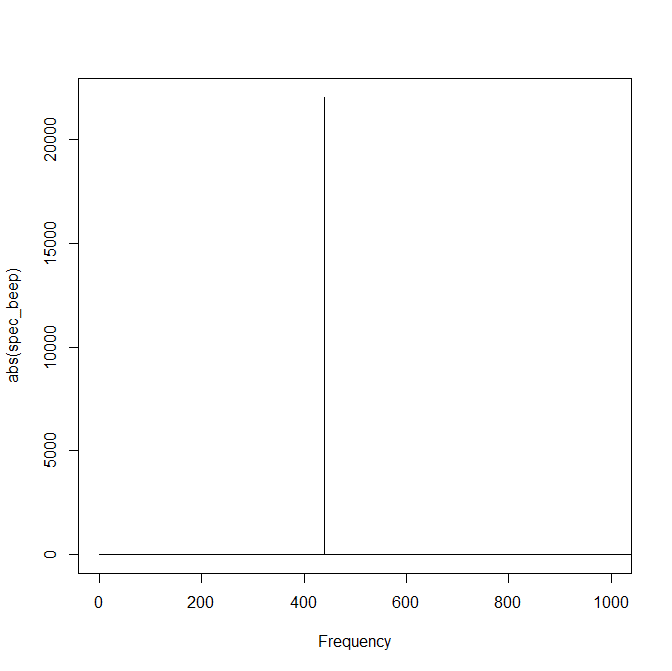

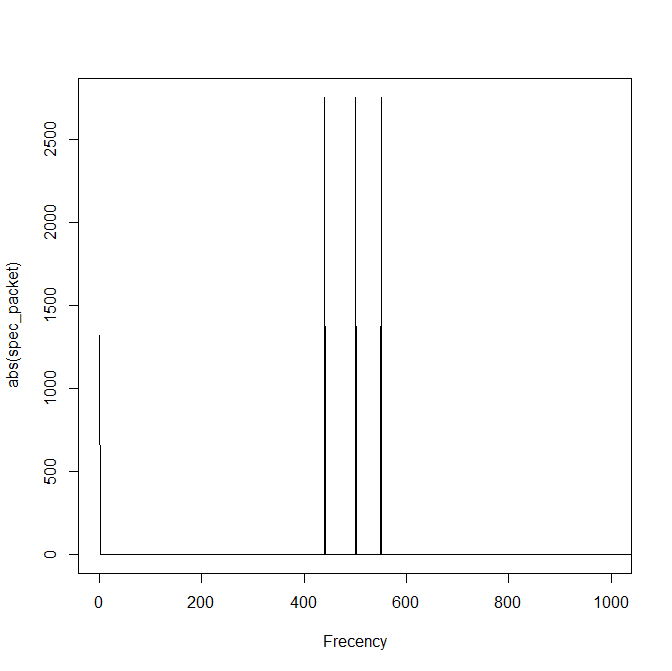
以上から、波動においては、「時間を確定するとエネルギーが不確定になり、エネルギーを確定すると時間が不確定になる」ことが分かりました。
ここで用いた考え方は、物理学の分野では「フーリエ変換法」と呼ばれています。20世紀には生物学で遺伝子の実体解明につかわれました(生命科学とフーリエ変換|高橋泰城 (note.com) )。
数学的には等価な方法は、確率論や統計学の分野では「特性関数」とよばれています。特性関数について知りたい人は下記のリンクをごらんください。
行動経済学 用語集 行動ファイナンス関連 特性関数 (高橋泰城 たかはし たいき)|高橋泰城 (note.com)
2回目講義のデモンストレーション その2 速算暗算術をRでやってみよう(数字の四則演算のRでの記号の紹介)



Rにおける数値の扱い

数値のコンピュータ内の表現の仕方について、情報処理技術者試験ではどういう問題が出題されるか興味がある方は↓
数値のコンピュータ内でのデジタル表現 応用情報技術者試験 例題|高橋泰城 (note.com)
2回目講義ではベクトルと行列も紹介します



・ここでは、ベクトルの「内積」をRで計算する関数(コマンド)を紹介しましたが、そういえばベクトルには「外積」という積もあった気がするけど、外積はどうやって計算するの?と疑問に思った人は以下のリンクの解説をご覧ください。
ベクトルの外積---Rならcross() Pythonならnp.cross()でどうぞ|高橋泰城 (note.com)
・Rで<-c()を使って作成したベクトルは縦ベクトルか横ベクトルか気になった人はここを参照してください。
・Rでベクトルの計算ができるようになると、量子力学におけるディラックのブラケットの計算もRでできるようになります。それに興味ある人はこちらをご覧ください。
講義3回目 記述統計(課題1と課題2を提出してもらいます)


ここで出てきた「不偏分散」(英語ではunbiased variance)とはどういうものか、復習(または初めて学習)したい人は以下の問題を解いてみて理解を深めましょう。
統計学入門:不偏分散の理解度チェック|高橋泰城(たかはしたいき) (note.com)
標本平均から母集団の分散を不偏推定した「不偏分散」は上記の問題で求まりました。それでは、母集団の平均(母平均)から母集団の分散を最尤推定するとどうなるでしょうか?それには以下の問題をやってみてください。
統計学入門:最尤推定の理解度チェック|高橋泰城(たかはしたいき) (note.com)
記述統計に関して、統計検定ではどんな問題が出題されるのかな?と思った方は↓をご覧ください。
統計検定対策1:記述統計---標準偏差、相関係数|高橋泰城 (note.com)
3回目の講義日には2変数の記述統計についても説明します。

統計検定では、2変数の分布に関してどんな問題が出題されるの?と思った方は以下をご覧ください。
統計検定対策 2----条件付確率、同時分布、周辺分布、条件付き期待値|高橋泰城 (note.com)
相関係数に関するさらなる説明は以下をご覧ください
外れ値が相関係数にどのように影響するか、数式を使って説明すると?|高橋泰城(たかはしたいき) (note.com)
標準偏差がほぼゼロだと相関係数はどうなるか?|高橋泰城(たかはしたいき) (note.com)
統計検定対策1:記述統計---標準偏差、相関係数|高橋泰城(たかはしたいき) (note.com)
講義4回目 確率論のおさらいや標本に関する概念の紹介、Rによるプログラミングの初歩など (課題3を提出してもらいます)



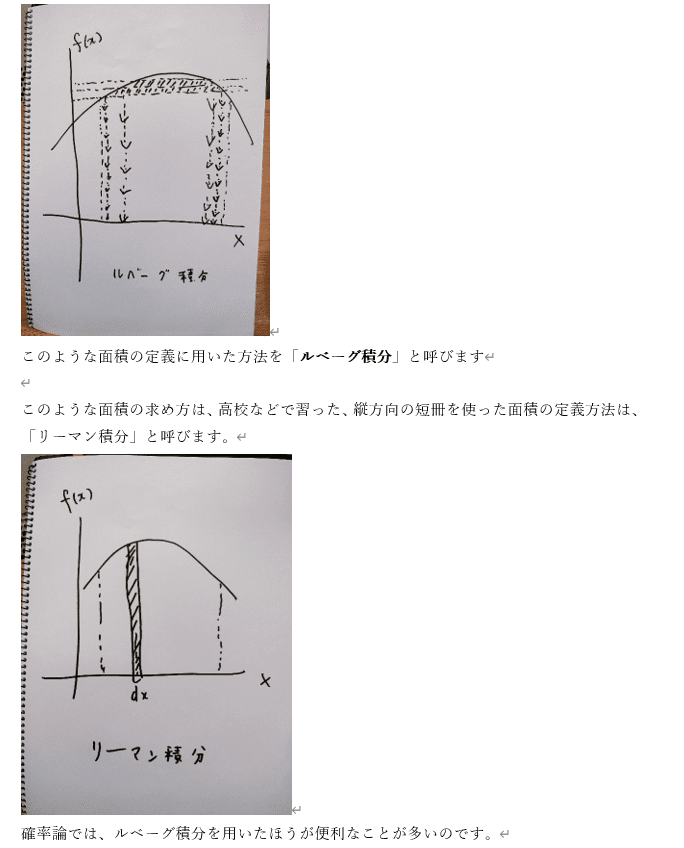

(下記ではピークのy座標が1になるようにy軸の目盛りが予め調整されているとします exp()はx=μで最大値1なので1/√2πσ^2で割る前にピークが1になっている必要があります また、正規分布では1σ内に68%が含まれることを利用しています)
ウィキペディアより:





正規分布に関する計算でよく用いられる「ガウス積分」の説明はこちらです
正規分布の計算のためのガウス積分の紹介|高橋泰城(たかはしたいき) (note.com)

仮説検定、有意水準、第一種の誤り、第二種の誤りなど関する理解を深めて実際の統計的仮説検定の際にどれくらいの標本サイズが必要かを考える以下の練習問題をやってみましょう(アクチュアリー試験レベル)
統計学入門:仮説検定や有意水準と標本サイズの理解度チェック問題|高橋泰城 (note.com)
Rで初めてプログラミングに触れる方へ
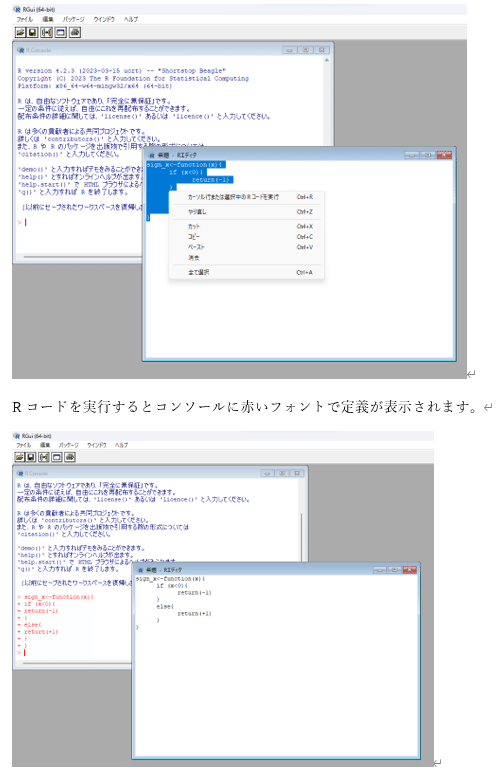
プログラムとはコンピュータに対する手順に基づいた命令のことです。構造化プログラミングにおいては、「順次」、「選択」、「繰り返し」という3つの命令の仕方(「制御構造」と呼びます)を使ってプログラムを作成します。Rにおいても、forをつかったループ文は「繰り返し」という制御構造を作成するのに都合がよいです。また、以下の図のように処理の手順を図解したものを「フローチャート」と呼びます。
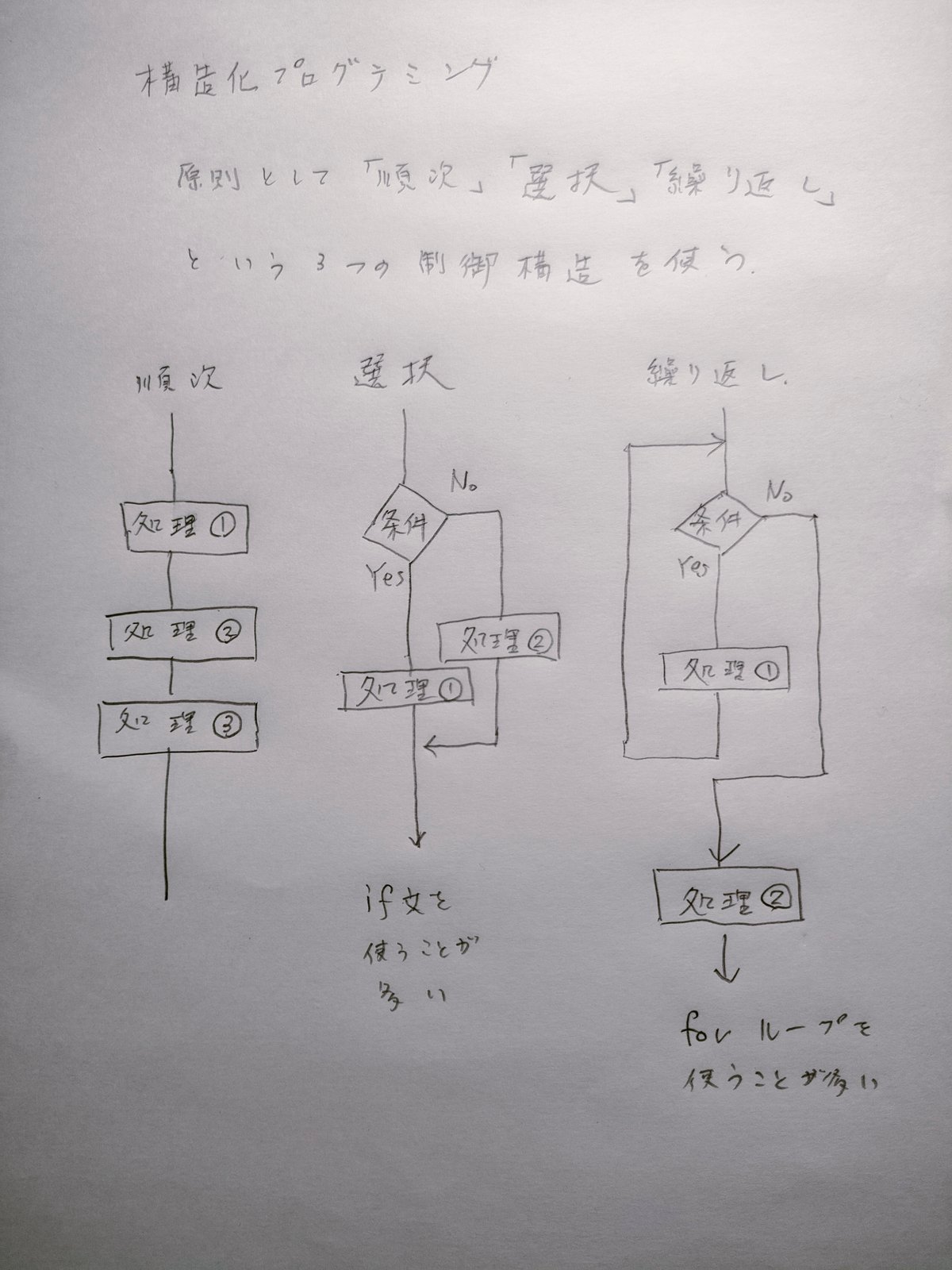
プログラミングは初めて、という方は、以下の「Rにおける関数やプログラミング入門」で、Rを用いて関数の定義やプログラミングの初歩に触れてみましょう。

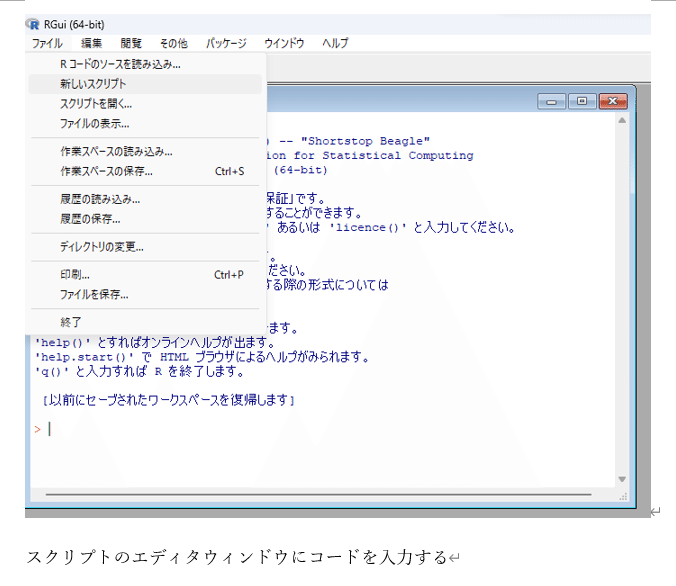
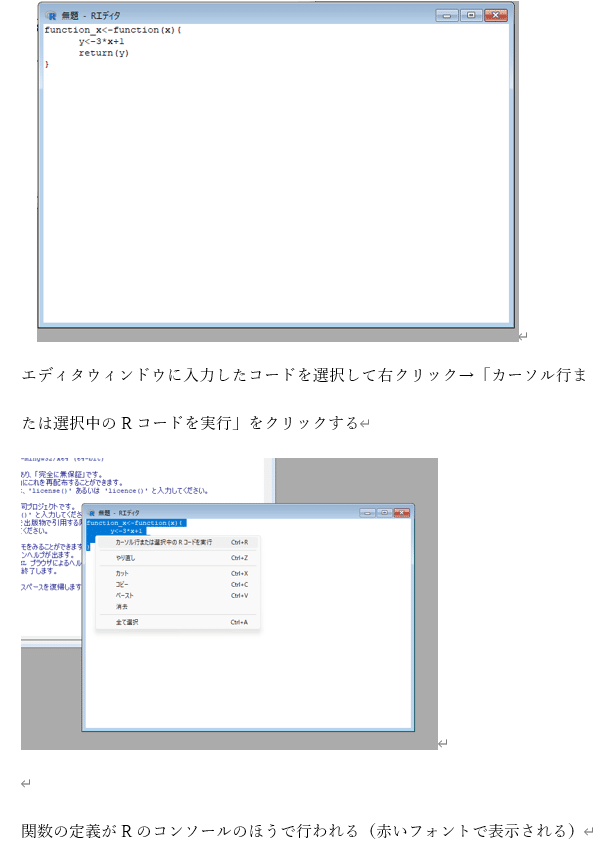
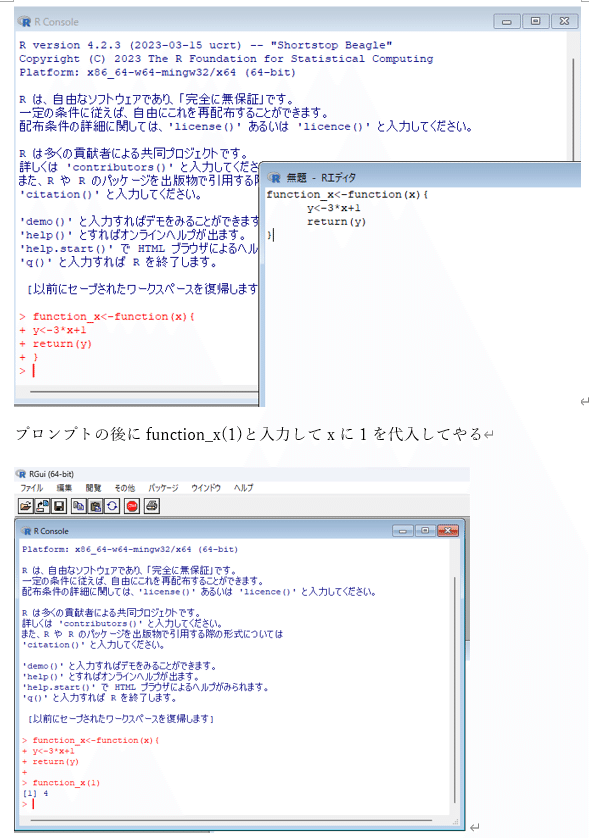

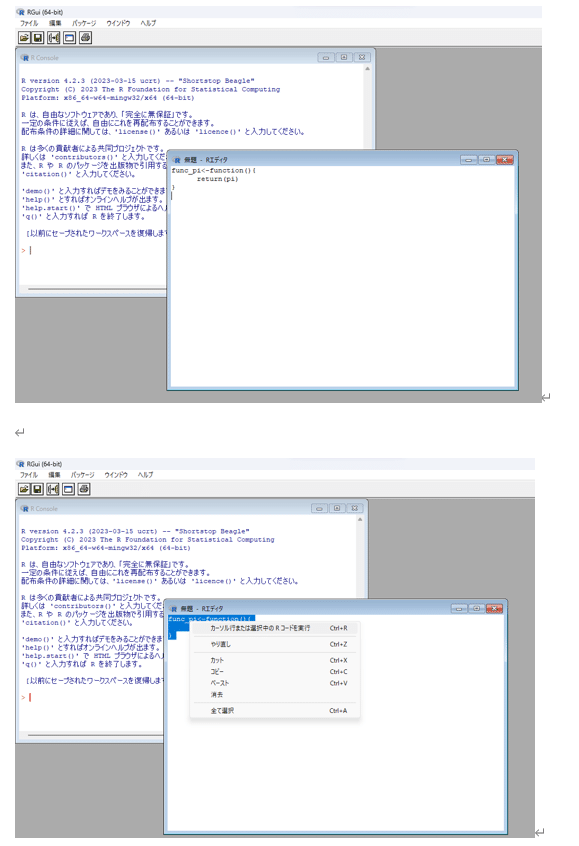
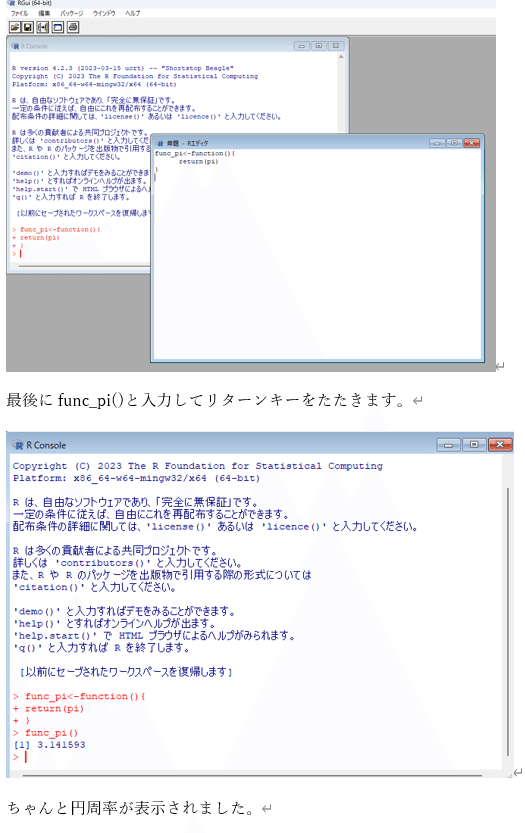


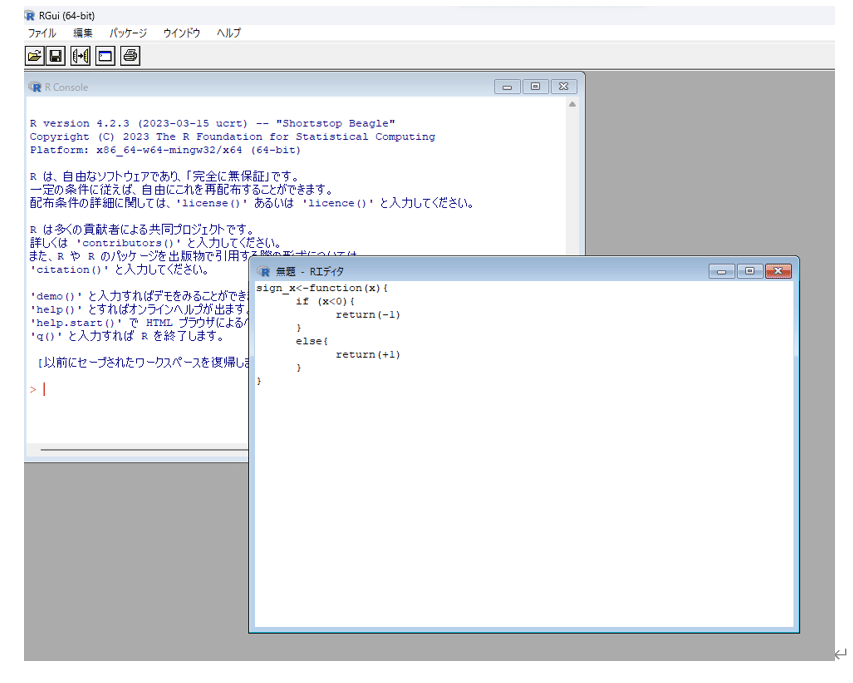


講義5回目 (習熟度テスト)
(学習したこと、文献調査したこと、シミュレーションや発表などしてもらいます)

コンピュータの歴史やフォン・ノイマン型アーキテクチャの説明の後、
https://note.com/api/v2/attachments/download/f3482e909bee937829b8c66dc41b84e5
や
https://note.com/api/v2/attachments/download/ac9a77eb587b55a809220582c1400de5
のファイルの内容を講義で解説し、実際にforループや条件分岐の動作を確認してもらいました。
Rでグラフを描くcurve---正規分布の確率密度関数の描画例|高橋泰城(たかはしたいき) (note.com)
Rにおけるnumeric関数の使用例|高橋泰城(たかはしたいき) (note.com)
Rにおけるrnormとdnormの違い|高橋泰城(たかはしたいき) (note.com)
Rによる中心極限定理のモンテカルロシミュレーション|高橋泰城(たかはしたいき) (note.com)
講義6回目 (大数の法則や中心極限定理とRによるモンテカルロシミュレーション入門①)
おさらい
講義7回目 (大数の法則や中心極限定理とRによるモンテカルロシミュレーション入門②)
おさらい
講義8回目 統計的仮説検定と正規分布から得られる確率分布①
標準正規分布からt分布をつくりだす|高橋泰城(たかはしたいき) (note.com)
標準正規分布からカイ2乗分布をつくる|高橋泰城(たかはしたいき) (note.com)
t検定(対応あり)|高橋泰城(たかはしたいき) (note.com)
講義9回目 正規分布から得られる確率分布②
-----------------------------------------------------------------------------------
以下は、成績評価用に提出してもらう課題(1-6)です:






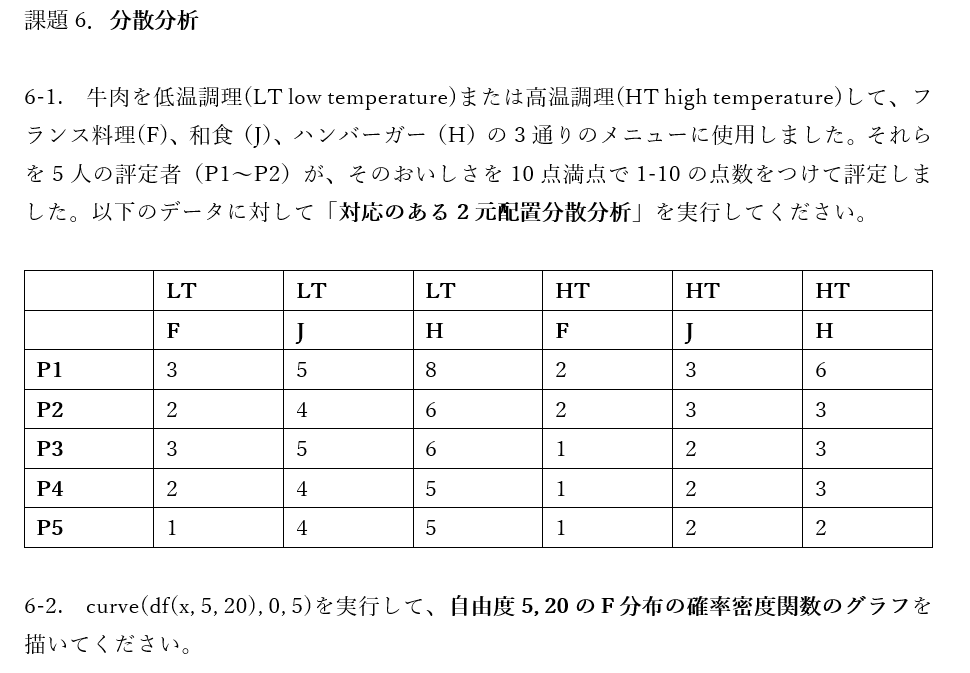
自分で考えてみたものを、以下の解答ファイルのコードと比べたりして考察したものを提出してください。
