VAE GAN VQVAE について
KLダイバージェンス(Kullback-Leibler Divergence)
KLダイバージェンスは、二つの確率分布の違いを測る方法です。一方の確率分布が、もう一方からどれだけ離れているかを示します。KLダイバージェンスが大きい場合、二つの分布はかなり異なると言えます。小さい場合は、似ていると言えます。この指標は、情報理論で使われるエントロピーの考え方を拡張したものです。
VAE(Variational Autoencoders)
VAEは、データを圧縮してから元に戻すオートエンコーダの一種です。VAEの特徴は、データを圧縮する際に、確率分布を使って表現する点です。VAEは、データを再構築する際の誤差と、圧縮されたデータの分布を正規化することを同時に行います。
KLダイバージェンスとVAE
VAEでは、KLダイバージェンスを使って、圧縮されたデータの分布を標準正規分布に近づけます。これにより、VAEはデータの生成方法を学び、新しいデータを作り出すことができます。
VAE(Variational Autoencoder)を最尤推定問題として定式化する際、以下のような式が用いられます。
まず、データセット

が与えられたとき、VAEの目的は、このデータセットが生成された確率
p(x)を最大化することです。しかし、直接p(x)を最大化することは難しいため、変分下限(Evidence Lower Bound: ELBO)を最大化することで、間接的にp(x)を最大化を目指します
以下の記事が非常にわかりやすいです
下記にも記載しますがあくまでもイメージですので
間違い等ありましたら ご指摘願います↓
変分下限(ELBO)は次のように定義されます:

ここで、
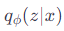
はエンコーダによって提供される潜在変数 z の近似事後分布です。

はデコーダによって提供される観測データ x の条件付き確率分布です。

は、近似事後分布と事前分布 p(z)との間のKLダイバージェンスです。
VAEの学習では、このELBOを最大化することにより、エンコーダのパラメータ ϕ とデコーダのパラメータ θ を同時に学習します。
変分下限は英語でELBO(evidence lower bound)や
(variational lower bound: VLB)と呼びます。
lower boundは下界ですから、
VLBは正確には変分下界と訳されるべきですが、
変分ベイズでは専らイェンセンの不等式により下界を導出することから、
下界を下限と呼ぶようになったと推察されます。
変分下界と呼ばれている書籍もありますが同義です
VAE(変分オートエンコーダ)におけるパラメータの最適化手順
データの尤度 p(x) を最大化するニューラルネットワークのパラメータ θ を最尤法によって求める。
扱いやすいように対数尤度logp(x) を最大化することを目標とする。
対数尤度 logp(x) を直接最大化することは積分の扱いが困難であるため、変分下限(ELBO: Evidence Lower Bound) L(θ,ϕ;x) を最大化することで、間接的に対数尤度を最大化する。
変分下限L(θ,ϕ;x) は以下のように定義されます:

ここで、第1項は再構築誤差
(再構築されたデータと元のデータの類似度)、
第2項はカルバック・ライブラー ダイバージェンス
DKL(qϕ(z∣x)∣∣p(z)) で、
潜在変数 z の事後分布 qϕ(z∣x) と
事前分布 p(z) との差異を表します。
カルバック・ライブラー ダイバージェンス
DKL(qϕ(z∣x)∣∣p(z)) は次のように3つの項に分解できます:
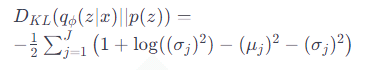
ここで、μj と σj はそれぞれz の事後分布の平均と標準偏差を表し、
J は潜在変数の次元数です。
この式は、潜在変数の事後分布が標準正規分布に近づくように
パラメータ θ と ϕ を最適化することを意味します。
上記の概要を簡単に報告します
VAE(変分オートエンコーダ)というのは、コンピューターがデータを理解して新しいデータを作るための方法の一つです。この方法を使うと、コンピューターはデータを簡単な形に変えて(これを「圧縮」と言います)、その後、その簡単な形から元のようなデータを作り出すことができます。
この方法で大切なのは、データをどのように圧縮して、どのように元に戻すかということです。VAEでは、データを圧縮するときに、ちょっとした工夫をして、データを「ランダム」に少し変えてみます。これによって、コンピューターはいろいろな可能性を考えながら学習することができます。
そして、コンピューターがデータを元に戻すときには、圧縮したデータが元のデータにどれだけ近いかをチェックします。これを「再構築誤差」と言います。また、圧縮したデータがランダムに変えた範囲内にあるかどうかもチェックします。これを「カルバック・ライブラー ダイバージェンス」と言います。
コンピューターは、再構築誤差を小さくして、カルバック・ライブラー ダイバージェンスも小さくするように学習します。これによって、コンピューターはデータを上手に圧縮して元に戻す方法を学ぶことができるのです。
ELBOについて簡単に
想像してみてください、あなたがお絵描きをしていて、その絵を友達に見せたいと思っています。でも、直接その絵を見せるのではなく、絵の「ヒント」を少しずつ友達に伝えて、友達がその絵を想像できるようにします。
ELBOは、その「ヒント」をどれだけ上手に伝えられるかを測る方法です。絵(データ)を直接見せるのではなく、絵の特徴(潜在変数)を上手に伝えることで、友達(デコーダ)が元の絵をうまく想像できるようにします。
そして、友達が想像した絵が本当の絵にどれだけ近いかを見て、ヒントの伝え方を少しずつ改善していきます。この「ヒントの伝え方」を改善することが、ELBOを最大化することに相当します。
つまり、ELBOは、絵のヒントを伝える上手さを測る方法で、それを使って、友達が元の絵をより正確に想像できるようにするための練習をします。
ELBO(証拠下界):
ELBOは、VAEの目的関数であり、モデルがデータをどれだけうまく再構築できるか(再構築誤差)と、潜在変数の事前分布と事後分布の間の類似性(KLダイバージェンス)のバランスを取ることを目指します。
ELBOを最大化することで、VAEはデータの再構築を改善し、同時に潜在空間の正則化を行います。
Reparameterization Trick(再パラメータ化トリック):
Reparameterization Trickは、VAEの潜在変数のサンプリングプロセスを微分可能にするための手法です。
このトリックにより、確率変数のサンプリングが微分可能な操作に変換され、VAEのネットワーク全体を通じて誤差逆伝播法を適用することが可能になります。
繋がり:
ELBOを最大化するためには、VAEのネットワークを通じて勾配を計算し、パラメータを更新する必要があります。
Reparameterization Trickは、ELBOの最適化過程において、潜在変数に関する勾配を計算することを可能にします。
つまり、Reparameterization TrickはELBOの最適化を実現するための重要な手段であり、VAEが効率的に学習を行うことを可能にするキーとなる技術です。
簡単に言えば、ELBOはVAEの学習目標を定義し、Reparameterization Trickはその目標に到達するための実用的な方法を提供します。
Reparameterization Trick
Reparameterization Trick(再パラメータ化トリック)は、変分オートエンコーダ(VAE)のような確率的なモデルで、確率変数のサンプリングプロセスを微分可能にするための手法です。このトリックは、モデルの学習中に誤差逆伝播法(バックプロパゲーション)を使用することを可能にします。
通常、VAEでは、入力データから潜在変数 z をサンプリングするために確率分布(例えば、正規分布)を使用します。しかし、このランダムなサンプリングプロセスは微分不可能であり、そのため、ネットワークを通じて誤差を逆伝播させることができません。
Reparameterization Trickでは、この問題を解決するために、確率変数 z のサンプリングを別の方法で行います。具体的には、まず標準正規分布からノイズ ε をサンプリングし、次にこのノイズを使って潜在変数 z を計算します。この計算は、通常、平均 μ と分散 σ^2 の関数として行われます。これにより、z の値はランダムなノイズ ε とモデルのパラメータに依存することになり、ネットワーク全体が微分可能になります。
この手法により、VAEは入力データから潜在変数 z を効果的に学習し、同時にデータの再構築を行うことができるようになります。Reparameterization Trickは、VAEが確率的な要素を含みながらも、効率的に学習を行うための重要な要素です。
GAN(Generative Adversarial Networks)
GANは、生成器と識別器の二つのネットワークを競争させることで学習します。生成器は本物のようなデータを作り出し、識別器は本物のデータと生成されたデータを区別しようとします。この競争を通じて、生成器はよりリアルなデータを作り出す能力を高めます。
JSダイバージェンス(Jensen-Shannon Divergence)
JSダイバージェンスは、二つの確率分布の類似度を測る指標で、KLダイバージェンスに基づいていますが、対称性を持つ点が特徴です。JSダイバージェンスは、二つの分布間の「距離」をより直感的に表現することができます。この指標は、特に生成モデルの分野で重要な役割を果たします。
GANの種類
DCGAN
DCGAN (Deep Convolutional Generative Adversarial Networks)
DCGANは、GANに対して畳み込みニューラルネットワーク(CNN)を適用し、
かつネットワークを深くした手法です。
DCGANの登場によって、より写真と見分けがつかない画像を生成することが可能となり、注目を集めました。
LAPGAN
LAPGAN, Denton et al. 2015
このLAPGAN(Laplacian Pyramid of Generative Adversarial Networks)はCNNを使ったモデルで、段階的により高解像度な画像を生成していくのが特徴です。
GANは学習が不安定という問題がありました。いきなり高解像度の画像を生成するのは難しいかもしれません。しかし、低解像度の画像を生成することは簡単でしょう。その低解像度画像を使って、もう少しだけ解像度の高い画像を生成することもそれほど難しくはないだろう、というのがLAPGANの主なアイディアです。これを繰り返していくことによって、最終的に解像度の高い画像を生成します。
infoGAN
InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
infoGANの構造
教師なし学習で生成画像を制御できそうなinfoGAN
Information Maximizing Generative Adversarial Networks (InfoGAN)
ノイズと観測の両方に調整を入れる機構を用いた学習
Conditionnal GAN
生成する画像を明示的に書き分けるために、訓練時に教師データのカテゴリ(ラベル)情報を用いてやろう、というのがconditional GAN
pix2pix
pix2pixとは、2017年に公開されたGANベースのスタイル変換モデルです。
pix2pixは、ある入力画像をもとに、異なる出力画像を生成することができます。
cycleGAN
CycleGANは、GANでスタイル変換を行う手法のひとつです。
こちらの手法、画期的なのが「適当なデータでも量さえあれば、
いいカンジに変換してくれる」というところ。
これまで主流だった「pix2pix」というスタイル変換手法では、塗り絵のように、輪郭がピッタリ合っているようなペア画像のみ変換可能。
一方、CycleGANは厳密なペアでなくても、柔軟に変換可能な手法です。
GANの学習にはテクニックがある
この論文は、GAN(Generative Adversarial Networks)の学習方法に関するもので、特に「Two time-scale Update Rule(TTUR)」という新しいアプローチを提案しています。このアプローチは、強化学習の一手法であるactor-critic学習から着想を得ています。
強化学習のActor-Critic学習とは?
強化学習では、行動を選択する「actor」とその行動の結果を評価する「critic」を使います。GANの構造と似ていて、GANのgeneratorがactor、discriminatorがcriticの役割を果たします。
TTURの主な内容
Discriminatorの高速学習:GANにおいて、discriminator(批評家)をgenerator(生成者)よりも速く学習させることで、学習が安定し、収束が早まることを示しています。
学習率の調整:WGAN-GP(Wasserstein GAN with Gradient Penalty)では、discriminatorをgeneratorよりも多く学習させていましたが、TTURでは、両者を同じ頻度で学習させ、discriminatorには大きな学習率を適用することで、学習がより効率的に進むことを示しています。
Frechet Inception Distance(FID)
新しい評価指標:GANが生成した画像の品質を評価する新しい指標として、FIDを提案しています。
FIDの特徴:FIDは、Inception v3モデルを使用して、教師データと生成画像の両方で識別ラベルの平均と分散を計算し、そのガウス分布の距離をFrechet距離で測定します。これにより、生成されたデータの多様性も評価することができます。
上記は一部のテクニックを紹介した論文でしたが
他にも 様々なテクニックがありますのでよろしければ確認願います
VQ-VAE(Vector Quantized Variational Autoencoder)
VQ-VAEは、VAEを拡張した2017年に発表されたモデルで、離散的なデータ表現を使います。VQ-VAEは、データを圧縮してから再構築する際に、連続的な表現ではなく、離散的な表現(ベクトル量子化)を使用します。
潜在変数を量子化(離散化するため)
DiscreteVAE (dVAE) と呼ばれる
VAEに比べて posterior collapse が起きにくいことが報告
潜在変数の量子化(DiscreteVAE)を簡単に表現
潜在変数の量子化:普通、コンピュータはデータをたくさんの数字(連続的な値)で表しますが、VQ-VAEでは、これらの数字をもっとシンプルな形(離散的な値、つまり決まったいくつかの数字のグループ)に変換します。これを「潜在変数の量子化」と言います。例えば、色を「赤」「青」「緑」のように単純なグループに分けるようなイメージです。
DiscreteVAE:このようにデータをシンプルなグループに分ける方法を「DiscreteVAE」と呼びます。これにより、コンピュータはデータをもっと簡単に理解し、新しいデータを作り出すことができます。
Posterior Collapseを簡単に表現
Posterior Collapse:通常のVAEという方法では、時々「posterior collapse」という問題が起きます。これは、コンピュータがデータの大切な特徴を見逃してしまい、うまく新しいデータを作り出せない状態を指します。つまり、コンピュータがデータを十分に理解できていない状態です。
VQ-VAEの利点:VQ-VAEは、データをシンプルなグループに分けることで、この「posterior collapse」の問題を解決します。つまり、コンピュータがデータをもっとしっかりと理解し、より良い新しいデータを作り出せるようになるのです。
VQ-VAEについて詳しく
VQ-VAEは、データを圧縮して新しいデータを生成するための技術です。このモデルでは、特に「ベクトル量子化」というプロセスが重要です。
VQ-VAEの構成要素
エンコーダ (Encoder):
入力データ x を潜在空間の連続的な表現 ze(x) に変換します。
ベクトル量子化 (Vector Quantization): エンコーダによって生成された連続的な潜在表現 ze(x) を、事前に定義された離散的なベクトルセット(コードブック) e にマッピングします。このプロセスにより、潜在表現は離散的な形式 zq(x) に変換されます。
デコーダ (Decoder): 離散的な潜在表現 zq(x) を元のデータ空間に再構築し、出力 x^ を生成します。
損失関数の勾配伝播
ベクトル量子化の損失関数:通常、損失関数は量子化前後のデータの差分で計算されますが、VQ-VAEでは少し違います。勾配(変化量)を計算する際に、特定の関数(stop_gradientのようなもの)を使って、一部の勾配の伝達を止めます。これは、計算が難しいため、勾配の伝達を簡単にするための工夫です。
損失関数の各項目の役割:損失関数には複数の項目があり、それぞれ異なる部分を更新します。一部の項目は「embedding行列」(データを圧縮するための行列)を更新し、他の項目は入力データ(Encoder)の更新に関与します。
argmin関数
argmin関数:これは、配列の中で最も小さい値がある位置(インデックス)を見つける関数です。ヘヴィサイドの階段関数を使って、この関数を表現することができますが、実際には微分が難しいため、stop_gradientのような関数を使って、この部分の計算を省略します。
embedding行列の役割:VQ-VAEでは、embedding行列は入力データを圧縮するためのものではなく、量子化されたデータを元の空間に戻すためのものです。
ベクトル量子化とSemantic Segmentationの類似点:VQ-VAEのベクトル量子化は、Semantic Segmentation(画像のピクセルごとに物体を認識する技術)と似ています。Semantic Segmentationではsoftmax関数を使いますが、VQ-VAEでは距離の二乗とargmin関数を使っています。
VQ-VAEにおける量子化プロセスは、エンコーダーが生成した連続的な潜在表現z(x)を、コードブック内の離散的なベクトルにマッピングすることで成立します。このプロセスの中心にあるのが、ekの選択です。ここで、ekはコードブック内の離散ベクトルを指し、その選択は次のように行われます

この式は、入力データxに対するエンコーダーの出力z(x)と、コードブック内の各ベクトルejとの間のユークリッド距離を計算し、その距離が最も小さいej(つまり、z(x)に最も近いコードブックベクトル)を選択します。選択されたekは、z(x)の量子化された表現として機能し、デコーダーへと渡されます。
この選択プロセスにより、連続値であるz(x)は、離散的な潜在空間の特定の点ekに「スナップ」されます。この量子化された潜在表現は、VQ-VAEが生成タスクで使用する離散的なコードとして機能し、デコーダーがこの離散的なコードを用いて最終的な出力(例えば、画像)を再構築します。
量子化の利点と課題
量子化プロセスの導入により、VQ-VAEは以下のような利点を持ちます:
表現の効率化: 離散的な潜在空間を用いることで、情報をより効率的に圧縮し、管理することが可能になります。
生成品質の向上: 量子化により、デコーダーがより一貫性のある、高品質な出力を生成することが容易になります。
一方で、量子化プロセスは学習中に特別な取り扱いを必要とします。具体的には、量子化による勾配の不連続性に対処するために、勾配の推定(straight-through estimator)などのテクニックが用いられます。これにより、モデル全体を効果的に学習させることができます。
量子化プロセスはVQ-VAEの中核をなす部分であり、このプロセスを通じて、VQ-VAEは従来のVAEや他の生成モデルとは異なる、ユニークなアプローチで物体検出や画像生成などのタスクを実行します。
VQ-VAEの論文
https://arxiv.org/pdf/1711.00937.pdf
van den Oord, A., Vinyals, O., & Kavukcuoglu, K. (2018). Neural Discrete Representation Learning. arXiv. https://arxiv.org/abs/1711.00937v2
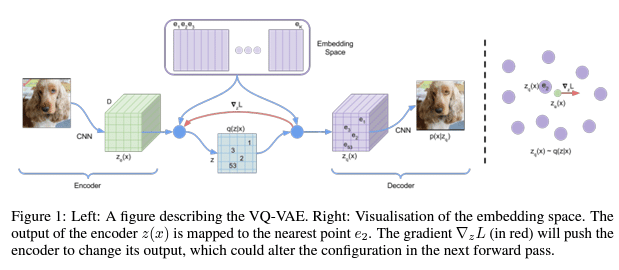
この図は、VQ-VAE(Vector Quantized Variational AutoEncoder、ベクトル量子化変分オートエンコーダ)という機械学習モデルを説明しているものです。このモデルは、画像などのデータを効果的に圧縮し、後でそのデータを再現することができます。
エンコーダー
CNN(畳み込みニューラルネットワーク): 画像から特徴を抽出するためのネットワークです。画像を入力として受け取り、それを数値の集まり(特徴マップ)に変換します。
エンベディングスペース(コードブック)
エンベディングスペース: データの特徴を代表する小さなパーツの集まりです。これらは、データを圧縮するための「辞書」のようなものです。
量子化プロセス
量子化: エンコーダーによって出力された特徴を、エンベディングスペースの中で最も近い点に割り当てるプロセスです。この図では、z(x)をe2に割り当てています。
勾配∇L
勾配 ∇L: モデルがどのように学習を進めるべきかを示す指標です。この図では赤い矢印で表されており、エンコーダーの出力を調整する方向を示しています。
デコーダー
デコーダー: 圧縮されたデータ(量子化された特徴)を元の画像に似たデータに復元するネットワークです。
この図全体としては、画像を特徴マップに変換し(エンコーダー)、その特徴マップをコードブックを使って圧縮し(量子化)、そして圧縮されたデータから元の画像を再構築する(デコーダー)というプロセスを表しています。VQ-VAEは特に、画像や音声などのデータを圧縮するのに有効な技術であり、データの生成や再構築に関するタスクによく使われます。
詳しくは以下のサイトがわかりやすいです
上記サイトの図を参照させていただきます
具体的な内容は上記サイト参照願います
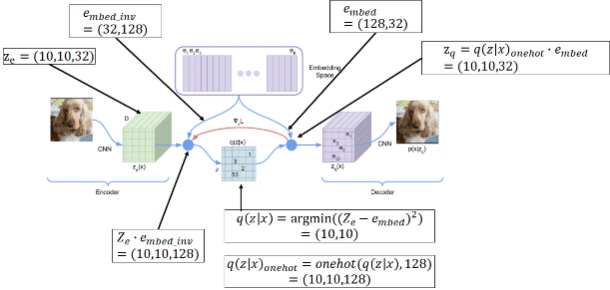
この図は、VQ-VAE(Vector Quantized Variational Autoencoder)という深層学習モデルのプロセスを示しています。VQ-VAEは、画像などのデータをコンパクトな形式に圧縮し、その後、元のデータに似たデータを再構築することができるモデルです。図の各部分を簡単に説明します。
エンコーダー
CNN: これは畳み込みニューラルネットワーク(Convolutional Neural Network)で、画像を入力として受け取り、その画像の特徴を抽出します。ここでの出力は Ze と示されていて、この例ではサイズが (10, 10, 32) の3次元の特徴マップです。
エンベディングスペース(コードブック)
エンベディング: これはモデルの中で、特徴ベクトル(Ze で表される)を、離散的な表現に変換するための「辞書」のようなものです。e embed は、エンベディングスペース(コードブック)のサイズが (128, 32) であることを示しています。
量子化プロセス
q(Z|x): この式は、エンコーダーの出力 Ze とエンベディングベクトル e embed との間で最も近いベクトルを見つけるプロセスを表しています。具体的には、Ze の各ベクトルがエンベディングスペースのどのベクトルに最も近いかを計算して、それをq(Z∣x) としています。この例では、(10,10) の位置が選ばれています。
デコーダー
デコードプロセス: 選択されたエンベディングベクトルは、デコーダーによって元の画像に似た出力を生成するために使われます。これにより、元の入力データと似たデータが再構築されます。
損失関数
損失: 図中には示されていませんが、VQ-VAEでは再構築された画像と元の画像との差異(損失)を測定し、モデルの性能を評価します。
その他のキー要素
e embed_inv: これはエンベディングスペースの逆行列を示しており、デコーダーで再構築する際に使用されます。
q(z∣x)onehot: 量子化されたエンベディングベクトルをone-hotエンコーディングすることで、デコーダーが理解できる形式に変換します。
Zq: one-hotエンコーディングされたエンベディングベクトルを実際のエンベディングベクトルに戻したものです。
この図は、VQ-VAEのプロセスを視覚的に理解するためのもので、高度なニューラルネットワークの操作を示しています。これにより、データの圧縮と再構築を行い、データ生成や表現学習に応用されます
van den Oord, A., Vinyals, O., & Kavukcuoglu, K. (2018). Neural Discrete Representation Learning. arXiv. https://arxiv.org/abs/1711.00937v2
の論文の式について再度確認してみます
VQ-VAE(Vector Quantized Variational AutoEncoder)モデルの損失関数

VQ-VAE 主なポイントと損失関数 (あくまでも私見)
エンコーダーの出力: モデルは画像などのデータを処理し、それを数値の集まり(特徴)に変換します。この変換を行う部分をエンコーダーと呼びます。
量子化: エンコーダーの出力を特定の数値の集まり(コードブック内のベクトル)に変換します。これにより、データは離散的な形で表現されます。
勾配: 学習中にモデルがどのように改善されるべきかを示す情報。勾配はエンコーダーの出力をより良くするために役立ちます。
損失関数: モデルの訓練に使用される関数で、3つの主要な部分から成り立っています。
再構成損失: デコーダーによって再構築されたデータが元のデータにどれだけ近いかを評価します。
埋め込み損失: エンコーダーの出力がコードブックのどのベクトルに最も近いかを評価します。
コミットメント損失: エンコーダーが出力する特徴がコードブックの特定のベクトルに強く寄り添うようにするためのものです。
数式の説明
数式(3)では、これら3つの部分がどのように組み合わされるかを示していますが、専門用語や数学的な記述を分かりやすくするために、以下のように説明できます。
モデルは、元のデータをどれだけよく再現できるか(再構成損失)、コードブックのベクトルとどれだけ適切に一致しているか(埋め込み損失)、そしてエンコーダーがそのコードブックのベクトルにしっかりと「コミット」(寄り添う)しているか(コミットメント損失)の3つの側面を考慮して学習します。
これらの側面を計算するために、モデルはエンコーダーからの出力とコードブックのベクトルを比較し、それらの差異を評価します。この差異が小さいほど、モデルが良いと評価されます。
もう少し具体的に説明しますと
VQ-VAE(Vector Quantized Variational AutoEncoder)モデルの損失関数を示しており、モデルが学習する際に最小化しようとする目標の量です。この損失関数は複数の項から構成されています。それぞれの項はモデルの異なる側面に対応しており、以下のように説明できます。
第一項: 再構成損失(Reconstruction Loss)
log p(x|z_q(x))は再構成損失を表し、VQ-VAEのデコーダーが生成した出力が元の入力データxにどれだけ近いかを測定します。この項目が小さいほど、再構成されたデータは元のデータに似ています。
第二項: 量子化損失(Quantization Loss)
二本線で囲まれた記号は、ベクトルのノルムを示しています。特に、二本線が使われている場合は、ユークリッドノルム(またはL2ノルム)を指していることが一般的です。ユークリッドノルムはベクトルの長さまたは大きさを表し、ベクトルの各成分の二乗和の平方根として計算されます。
たとえば、
ベクトル v に対してユークリッドノルムは次のように計算されます:
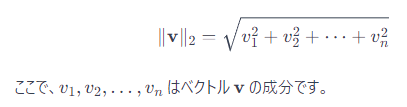
||sg[z_e(x)] - e||^2は量子化損失を表し、エンコーダーの出力z_e(x)とコードブックeのベクトルとの距離を測定します。sgは勾配を止める(stop-gradient)操作を意味し、この操作によってこの項での損失はコードブックのベクトルeの学習にのみ影響し、エンコーダーのパラメーターには影響しません。
第三項: コミットメント損失(Commitment Loss)
β||z_e(x) - sg[e]||^2はコミットメント損失を表し、エンコーダーの出力がコードブックのベクトルに「コミット」すること、つまり選択されたコードブックのベクトルeに近づくようにエンコーダーを強制します。βはこの項の重みを調整するハイパーパラメーターで、コミットメント損失の影響を大きくしたり小さくしたりします。
コードブックとコミットメント損失について
コードブック: コードブックはエンベディングスペース内の固定されたベクトルの集合で、エンコーダーの出力を量子化するために使用されます。エンコーダーの出力がコードブックの特定のベクトルにマッピングされることで、連続的なデータを離散的な表現に変換します。
コミットメント損失: コミットメント損失は、エンコーダーが選択したコードブックのベクトルに責任を持たせるためのものです。これにより、エンコーダーはコードブックのベクトルをより正確に表現するようになり、デコーダーがより良い再構成を行えるようになります。

ストップグラディエント演算子の使用について説明している部分で、これは計算の前進時に更新されない変数を制約する役割があります。
また、エンコーダーとデコーダーが異なる損失関数を最適化するプロセスについて言及しており、β(ベータ)パラメータを用いた正則化が議論されています。さらに、潜在変数zに一様事前分布を仮定しているため、ELBO(エビデンス・ロウアー・バウンド)に通常現れるKL発散項は一定で、エンコーダーのパラメータに関しては無視できるとしています。モデルはN個の離散潜在変数を定義し、画像ネットやCIFAR10において32x32の潜在変数を用いた実験を行っていることも述べられています。最後に、デコーダーはMAP推定からのzに基づいて訓練されるため、それ以外のzに確率質量を割り当てるべきではないと結論付けています。
先ほどの数式は、確率の概念を使って、あるデータが生成される確率を計算する方法を示しています。この式の理解を助けるために、確率に関連するいくつかの基本的な概念を説明します。
まず、「logp(x)」は、データxが観測される確率の対数を意味します。対数を取ることは、計算を簡単にしたり、数値のオーダーが非常に大きいまたは小さいときに扱いやすくするためによく行われます。
次に、シグマ記号(Σ)は、全ての可能なkに対して合計することを意味します。ここでのkは、データxを生成する過程であり、様々な方法でデータxが生成される可能性を表しています。
式の中で、「p(zk∣x)」は、与えられたデータxが観測されたときに、
あるプロセスkによってデータが生成される条件付き確率を示しています。一方、「p(zk)」は、そのプロセスk自体が起こる確率を意味しています。
合計することで、データxが生成される全ての異なる方法の確率を考慮して、データxが観測される全体の確率を計算しています。
この数式は、「ある特定のデータがどれくらいの確率で起こるか」を計算するためのものです。たとえば、サイコロを投げたときにどの目が出るかを考えるようなもので、データxはサイコロの目、kはサイコロの各面を意味しています。それぞれのサイコロの面が出る確率を全部足し合わせることで、最終的にサイコロを投げたときに特定の目xが出る確率を計算しています。対数を取る理由は、これらの確率が非常に小さいときに、計算を単純化しやすくするためです。
