
強化学習
強化学習は、機械学習の一分野であり、エージェントが環境と相互作用しながら最適な行動方針を学習する方法です。このプロセスは、人間が試行錯誤を通じて学習する方法に似ています。エージェントは、定義された報酬に基づき、環境からのフィードバックを受け取りながら、最適な行動を学習します。ここで、報酬をどのように定義するかが、学習プロセスの成否に重要な役割を果たします。
強化学習のモデル
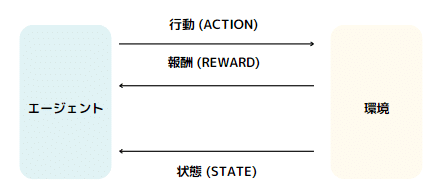
強化学習は、エージェントが最適な行動を学習するために環境との相互作用を通じて報酬を最大化しようとするプロセスです。
エージェント
エージェントは学習を行う主体で、環境に対して行動を選択し実行します。エージェントの目的は、環境から得られる報酬を最大化することにより、最適な行動方針(ポリシー)を学習することです。
環境
環境はエージェントが存在し、行動する場で、エージェントの行動に応じて変化します。環境はエージェントに対して報酬を提供し、エージェントの現在の状態に関する情報をフィードバックします。
報酬 (Reward)
報酬はエージェントの行動の結果として環境から提供されるフィードバックです。報酬は、エージェントが目指すべき目標を示し、学習プロセスを通じて最適な行動を導きます。
状態 (State)
状態はエージェントがその時点で認識している環境の状況を表します。エージェントは現在の状態に基づいて行動を選択します。
行動 (Action)
行動はエージェントが状態に応じて選択できる具体的な操作です。エージェントの行動選択は、その後の環境の状態と報酬に影響を与えます。

方策 (Policy)
方策は、特定の状態においてエージェントがどの行動を選択するかを定義するルールです。エージェントの目標は、報酬を最大化する方策を見つけることです。
行動価値関数(Value Function)
ある状態での行動の評価値を定める関数です。状態数が少ない時にはテーブル(表)で表記できます。主な手法に、Q学習におけるQ関数などがあります。
強化学習のプロセスでは、エージェントは繰り返し環境と相互作用し、行動の結果として得られる報酬に基づいて学習を進めます。
この過程で、エージェントは最適な行動方針を発見し、複雑な問題解決や意思決定タスクに対処する能力を向上させます。
強化学習を構築する過程
強化学習を構築する過程は、理解しやすい手順に分けられます。ここでは、その4つの基本的なステップについて説明します。
1. 環境を作る
強化学習では、エージェントが行動する「環境」を最初に設定します。この環境は、リアルな物理世界を模倣したものか、コンピュータ上で作成された仮想世界のどちらかです。環境はエージェントにとっての学習場所となり、ここでの体験を通じて学習が進みます。
2. 報酬を定義する
次に、エージェントの行動に対する「報酬」を定義します。報酬はエージェントがどのような行動を取るべきかを学ぶための指標となります。良い行動には正の報酬を、望ましくない行動には負の報酬を設定することで、エージェントは目標達成に向けて最適な行動を学んでいきます。
3. エージェントを作成する
環境と報酬が設定されたら、次は「エージェント」を作成します。
エージェントは行動を決定する「方策(ポリシー)」と、
学習を進めるための「アルゴリズム」から構成されます。
方策は環境の状態に基づいて最適な行動を選択するルールです。
アルゴリズムには、Q-Learning、SARSA、モンテカルロ法などがあり、
これらはエージェントが経験から学習する方法を定めます。
4. エージェントの学習と検証を開始する
すべてが準備できたら、エージェントの学習を開始します。エージェントは方策に従って環境内で行動し、その結果として報酬を受け取ります。受け取った報酬を基に方策を調整し、より良い結果を目指して再び行動します。このサイクルを繰り返すことで、エージェントは徐々に最適な行動パターンを学習していきます。
強化学習は、多くの試行錯誤を必要とするため、効率的な学習には大量のデータや繰り返しのプロセスが求められます。しかし、この手法は複雑な問題解決に非常に有効であり、ゲーム、ロボット工学、金融など幅広い分野での応用が期待されています。
強化学習アプローチの概観
強化学習のアプローチは大きく分けて三つあります:価値反復法、方策勾配法、そして両方を組み合わせたアプローチです。
1. 価値反復法
このアプローチでは、エージェントは行動価値(Q値)を学習します。Q値とは、特定の状態で特定の行動を取った場合の予想報酬です。Q学習、SARSA、DQN(Deep Q-Network)、Rainbowなどのアルゴリズムがこのカテゴリに属します。
価値反復法とは?
価値反復法は、ある環境内でのエージェント(この場合は行動を選択するプログラムやロボット)が、最も良い結果を出す行動を見つけるための方法です。ここで言う「最も良い結果」とは、エージェントが得られる報酬(ポイントや得点など)を最大化することを意味します。
この方法では、「価値が最大となる行動を選択する」という考え方を基にしています。つまり、エージェントは現在の状態から、将来にわたって最も多くの報酬を得られる行動を選ぼうとします。
具体的な説明
価値反復法で使われる式を理解するために、以下の概念を簡単に説明します:
状態(s):エージェントがいる場所や状況です。
行動(a):エージェントが選択できる動作(例:左に移動する、ジャンプするなど)。
報酬(R):特定の行動を取った結果としてエージェントが得るポイント。
状態遷移確率(P):ある行動をとった際に、次の状態に移る確率です。
割引率(γ):将来の報酬を現在の価値に換算するための係数。将来の報酬をどれだけ重視するかを決めます。
式
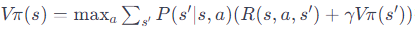
を分解してみましょう
Vπ(s):状態sにおける最大の予想される報酬(価値)。
max a:すべての可能な行動aの中から、最大の価値をもたらす行動を選びます。
Σs' P(s'|s,a):行動aをとった後に、各可能な次の状態s'に移る確率を合計します。
R(s,a,s'):状態sで行動aをとり、状態s'に移ったときの報酬。
γVπ(s'):次の状態s'から将来にわたって得られる予想される報酬の現在価値。
より簡単に言い換えると
エージェントは、自分が今いる状態から、どの行動を選ぶと将来的に最も多くの報酬を得られるかを考えます。この判断をする際に、今すぐ得られる報酬だけでなく、その行動を取った後にどんな状況になり、それから得られる報酬も考慮に入れます。将来の報酬は時間が経つにつれて価値が少し減ると考えるため、割引率を使って計算します。
この方法を繰り返すことで、エージェントはどの状態でどの行動を取れば最終的に最も多くの報酬を得られるかを学習していきます。
少し具体的に
各ステップをさらに簡単に説明しましょう。
ステップ1: 初期化
まず、すべての状態の価値を初期化します。これは、エージェントがまだ何も学習していないという意味で、全ての状態に対して価値V(s)を0に設定します。ここでいう「状態」とは、エージェントが取りうるあらゆる場所や状況のことです。
ステップ2: 繰り返し処理
このステップでは、エージェントが学習を進めるための繰り返し処理を行います。具体的には、以下のような処理を繰り返します。
変化量Δの初期化:この変数は、繰り返しの各ステップで価値V(s)がどれだけ変化したかを追跡します。最初は0に設定されます。
全ての状態sに対して:システム内の全ての可能な状態を順に見ていきます。
a. 現在の価値を保存:現在の状態の価値V(s)を一時的な変数vに保存します。
b. 価値の更新:各状態について、可能な全ての行動aを考慮し、その行動から得られる予想報酬の合計(現在の報酬と将来の報酬の割引された値)が最大になるように価値V(s)を更新します。
c. 最大変化量の更新:このステップで価値がどれだけ変わったか(vと更新後のV(s)の差)を見て、それがこれまでの繰り返しでの最大の変化量よりも大きい場合は、Δを更新します。
終了条件のチェック:Δがある小さな値θよりも小さくなったら、学習プロセスを終了します。θは、価値の更新が十分に小さくなったことを示す閾値です。
具体的な説明
このアルゴリズムは、エージェントが最適な行動を学習するために、環境内の各状態の価値を反復的に更新するプロセスです。繰り返しごとに、エージェントは「この状態でこの行動を取れば、即時の報酬と将来得られる報酬の合計が最大になる」という計算を全ての状態と行動について行います。そして、学習が進むにつれて、エージェントはより良い行動選択に基づく価値の推定値に徐々に近づいていきます。
このプロセスは、エージェントが「自分が今いる状態で何をすれば最終的に最も多くの報酬を得られるか」という問いに対する答えを見つけるのに役立ちます。そして、全ての状態に対してその答えがほとんど変わらなくなったとき、学習は完成です。
価値ベースとは?
価値ベースのアルゴリズムでは、エージェントの行動方策は明示されません。代わりに、各行動や状態の価値を推定し、最も価値が高いと推定される行動を選択するようにエージェントを訓練します。このカテゴリには、Q学習やSarsaなどが含まれます。
価値反復法に基づく様々なアルゴリズム
Q学習系
Q学習: 基本的な価値反復法の一つで、TD誤差(Temporal Difference error)を用いて価値関数を更新します。この方法は方策オフ(policy-off)であり、つまり、実際に選ばれた行動ではなく、可能な行動の中で最も良い価値を与える行動を選んで価値関数を更新します。Q学習は、適切な学習率が設定されると価値関数が収束すると証明されています。
DQN (Deep Q-Network): Q学習を深層学習に応用したもので、価値関数をニューラルネットワークでモデリングします。DQNの特徴は、学習を安定させるための経験再生(Experience Replay)というテクニックにあります。経験再生を利用することで、サンプル間の相関を減らし、より安定した学習を実現します。
優先度付き経験再生: DQNで使用される経験再生を発展させたもので、損失関数が大きいサンプルを優先的に学習します。
デュエリングネットワーク: 価値関数を状態価値関数とアドバンテージ関数に分けて学習させる手法です。
DoubleDQN: 通常のDQNが過大評価の傾向にある問題を解決するために提案されました。選ばれた行動を過去の重みで評価することで、過大評価を防ぎます。
SARSA
SARSA: 価値反復法の一つで、実際に取られた行動を用いて価値関数を更新する方策オン(policy-on)のTD学習です。SARSAは、局所解に陥りにくいとされていますが、Q学習に比べて収束が遅い場合があります。
その他のアルゴリズム
Gorila: DQNを分散処理によって高速化したアルゴリズムです。
Ape-X: 優先度付き経験再生を分散処理で高速化したアルゴリズムです。
R2D2: LSTMと経験再生と分散学習を組み合わせたアルゴリズムで、経験再生とLSTMの相性問題を解決しました。
これらのアルゴリズムは、強化学習における異なる問題点に対処するために開発されました。例えば、DQNは深層学習を取り入れることで複雑な問題を扱う能力を高めていますが、経験再生により学習の安定性を保持しています。
2. 方策勾配法
方策勾配法では、エージェントは直接的に行動方針(方策)を学習します。この方法は、エージェントがどの行動を取るべきかを直接的にモデル化することに焦点を当てています。
方策勾配法は、エージェントが最適な行動を学習するための方法の一つです。エージェントが行動することで得られる「報酬」を最大にするような行動パターンを見つけることが目標です。
方策勾配法の基本概念
方策: エージェントがどのような行動を取るかのルールやパターンです。これは、エージェントがどのような状況にあるかに基づいて、どの行動を選ぶべきかを決定します。
確率的方策: 方策が確率的であるとは、同じ状況でも異なる行動を取る可能性があるということです。つまり、完全に予測可能ではなく、ある程度のランダム性があるということです。
方策関数: 方策を決定するために使用される数学的な関数で、エージェントの状況(状態)を入力として、どの行動を取るべきかの確率を出力します。この関数はパラメータに依存しており、これを変更することでエージェントの行動を調整できます。
モデル化: 方策関数をどのように数学的に表現するかです。ニューラルネットワークなどの機械学習モデルを用いて方策関数を表現します。
状態価値関数: ある状態からスタートしたときに、これから得られると予測される報酬の合計です。将来得られる報酬には割引率が適用され、遠い未来の報酬は現在の価値よりも少なく見積もられます。
方策勾配法のプロセス
初期状態: エージェントはある初期状態からスタートします。
行動: エージェントは方策関数に基づいて行動を選びます。
報酬: その行動によって得られる即時報酬を受け取ります。
状態遷移: 行動によって次の状態に移行します。
目的関数の最大化: エージェントは目的関数を最大化するように方策関数のパラメータを調整します。目的関数は、初期状態から得られる報酬の期待値です。
方策反復法(Policy Iteration)は、強化学習の一手法で、エージェントの行動選択が方策(ポリシー)に基づいて行われ、この方策を繰り返し改善することで最適な方策を求めるアプローチです。この方法は、方策を直接的に更新していく「policyベース」の手法と呼ばれます。以下に、方策反復法のアルゴリズムを具体的に説明します。
アルゴリズムのステップ
ステップ1: 初期化
V(s)(各状態の価値)とπ(a|s)(ある状態で特定の行動を選択する方策)を初期化します。通常、V(s)は0で初期化され、π(a|s)は全ての行動が等しく選ばれる一様分布で初期化されます。
ステップ2: 方策評価 (Policy Evaluation)
方策に基づく各状態の価値を計算します。これは、現在の方策がどれだけ良いかを評価するステップです。
Δ=0で初期化し、全ての状態sに対して次を繰り返します。
現在の状態の価値V(s)を一時的な変数vに保存します。
新しい価値V(s)を、現在の方策π(a|s)に従って選ばれた行動と、その行動による報酬及び次の状態の価値の合計から計算します。
Δを、vと更新後のV(s)の差の絶対値と、前のΔの最大値で更新します。
Δがある小さな閾値θより小さくなるまでこのプロセスを繰り返します。
ステップ3: 方策改善 (Policy Improvement)
評価した価値に基づいて、方策を改善します。これは、より良い行動選択によって方策を更新するステップです。
方策が安定しているかどうかを追跡するために、policy_stableをTrueに設定します。
全ての状態sに対して、現在の方策π(a|s)で選ばれる行動aを見直し、最大の報酬をもたらす行動に基づいて方策を更新します。
もし現在の行動aが更新された方策で選ばれる行動と異なるならば、policy_stableをFalseに設定します。
方策が安定している(つまり、どの状態の方策も更新されない)場合、アルゴリズムは停止し、最適な価値Vと方策πを返します。そうでなければ、ステップ2に戻ります。
簡単に言うと
方策反復法では、まず現在の方策に基づいて状態の価値を評価し、その後でその価値をもとに方策を改善していきます。この評価と改善のサイクルを繰り返すことで、最終的に最適な方策を見つけ出します。このプロセスは、エージェントが環境内で最も報酬を得られる行動をどのように選ぶべきかを学習することにより、最適な行動戦略を導き出します。
方策勾配法の更新式は、エージェントがどのようにしてより良い行動を学習するか、つまり、その行動を取ったときにより多くの報酬を得られるようにするかを定めた数学的な手続きです。
目的関数の最大化
エージェントの目標は、与えられた環境で最大の報酬を得られるような行動方策を見つけることです。目的関数は、エージェントが行動を取るたびに得られる報酬の総和を表し、これを最大化したいと考えています。
勾配法とは
勾配法は、目的関数の最大値を探すための一般的な方法で、方策のパラメータを少しずつ調整していくことで、最終的に目的関数が最大となる点を見つけます。この過程では、目的関数の勾配(すなわち、その点での最も急な上昇方向)を計算し、その方向にパラメータを少しずつ動かしていきます。
方策勾配法の更新式
方策勾配法の更新式は、エージェントの方策パラメータを更新するためのルールです。数式で表すと以下のようになります。

符号がプラスになっているのは、最大化問題を解いているためです。最小化問題では符号がマイナスになりますが、ここでは最大の報酬を目指しているためプラスになります。
方策勾配定理
方策勾配定理は、この勾配を計算するための理論的な基盤を提供します。つまり、目的関数の勾配をどのように計算するかを示しており、勾配法において非常に重要な役割を果たします。
方策勾配定理は、強化学習においてエージェントが最適な行動を学習するためにどのように方策(行動を選択するルール)を更新するかを示す重要な理論です。この定理は、方策のパラメータを微小に変更したときに、期待される報酬(目的関数)がどのように変化するかを表す勾配(方向と大きさ)を提供します。
方策勾配定理の主要概念
方策勾配: 方策をパラメータ化した関数に対する勾配です。これは、エージェントが行動を選択する際に従う方策を最適化するために必要な、パラメータの変化の方向を示します。
行動価値関数 Q(s,a): 特定の状態 s で行動 a を取った際に、将来得られると予想される報酬の合計です。これは、その行動がどれだけ良い結果につながるかを数値化したものです。
訪問頻度 dπ(s): 方策 π に従ってエージェントが状態 s を訪れる頻度です。これは、エージェントがどのくらいの割合でその状態に到達するかを示します。
方策勾配定理の式
方策勾配は、次のような式で表されます:
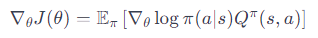
または、状態遷移の確率を考慮に入れた形で:
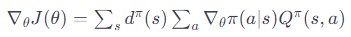
ここで、
∇θJ(θ) は方策のパラメータ θ に関する目的関数 J の勾配です。
∇θlogπ(a∣s) は方策の確率の対数の勾配で、方策がどのように行動選択の確率に影響を与えるかを示します。
Qπ(s,a) は、方策 π 下での行動価値関数です。
dπ(s) は、方策 π 下での状態 s の訪問頻度です。
方策勾配定理の意味
この定理は、最適な方策へと進むために方策のパラメータをどのように更新すれば良いかを示しています。具体的には、方策のパラメータを少し変えることで、期待される報酬が最も増加する方向を教えてくれます。強化学習のアルゴリズムは、この勾配に従って方策のパラメータを更新し、エージェントがより多くの報酬を得られるような行動を選択することを学びます。
方策勾配定理は、強化学習においてエージェントが最適な行動を学習するためにどのように方策(行動を選択するルール)を更新するかを示す重要な理論です。この定理は、方策のパラメータを微小に変更したときに、期待される報酬(目的関数)がどのように変化するかを表す勾配(方向と大きさ)を提供します。
方策勾配定理の主要概念
方策勾配: 方策をパラメータ化した関数に対する勾配です。これは、エージェントが行動を選択する際に従う方策を最適化するために必要な、パラメータの変化の方向を示します。
状態価値関数 V(s): これはエージェントがある状態 s にいるときに、これから得られると予想される報酬の総和です。この関数は、エージェントが将来どれだけの報酬を得られるかを示します。
行動価値関数 Q(s,a): 特定の状態 s で行動 a を取った際に、将来得られると予想される報酬の合計です。これは、その行動がどれだけ良い結果につながるかを数値化したものです。
訪問頻度 dπ(s): 方策 π に従ってエージェントが状態 s を訪れる頻度です。これは、エージェントがどのくらいの割合でその状態に到達するかを示します。
確率的方策 π(a∣s;θ): エージェントが状態 s にいるときに行動 a を選ぶ確率を、パラメータ θ を使ってモデル化した関数です。
方策勾配定理によると、エージェントのパラメータ θ を少しずつ変更することで、エージェントの行動が良い結果につながる方向に誘導できるとされています。具体的には、行動価値関数 Q と確率的方策 π の関係を利用して、どのようにパラメータ θ を更新するか計算します。
方策勾配定理の式
方策勾配は、次のような式で表されます:
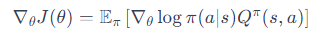
または、状態遷移の確率を考慮に入れた形で:
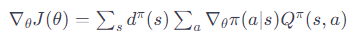
ここで、
∇θJ(θ) は方策のパラメータ θ に関する目的関数 J の勾配です。
∇θlogπ(a∣s) は方策の確率の対数の勾配で、方策がどのように行動選択の確率に影響を与えるかを示します。
Qπ(s,a) は、方策 π 下での行動価値関数です。
dπ(s) は、方策 π 下での状態 s の訪問頻度です。
方策勾配定理の意味
この定理は、最適な方策へと進むために方策のパラメータをどのように更新すれば良いかを示しています。具体的には、方策のパラメータを少し変えることで、期待される報酬が最も増加する方向を教えてくれます。強化学習のアルゴリズムは、この勾配に従って方策のパラメータを更新し、エージェントがより多くの報酬を得られるような行動を選択することを学びます。
方策ベースとは?
方策ベースのアルゴリズムでは、エージェントの行動方策(どのように行動を選択するかのルール)を直接的に最適化します。価値関数は存在するものの、これは方策を改善するための参考情報として内部で利用されるだけで、直接行動選択には利用されません。代表的な方策ベースのアルゴリズムには、REINFORCEやA3C(Actor-Critic)があります。
アルゴリズムの比較
REINFORCE: 方策勾配法の一種で、行動方策のパラメータを直接更新します。勾配計算にはエピソード全体の報酬が使われます(モンテカルロ法)。
覚え方:雨で 豊作 米は モンキーのテ カル ロ
豊作勾配の分散を減らすためにベースラインb(s)を導入
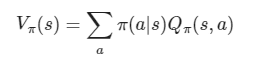
状態sにおけるポリシーπの下での価値関数Vπ(s)を示すベルマン方程式が記されています。この方程式は強化学習の分野で用いられ、エージェントがある方策(ポリシー)に従って行動したときの期待される報酬の総和を表しています。
ここで、Vπ(s)は状態sにおける価値関数であり、エージェントが状態sから始めて方策πに従って行動した場合の期待される報酬の総和を意味します。方程式内の∑は、全ての可能な行動aについての合計を取ることを示しています。
π(a∣s)は、状態sにおいて行動aを取る確率を表す方策の確率分布です。つまり、エージェントがある状態でどの行動をどれだけの確率で選ぶかを示します。
Qπ(s,a)は行動価値関数であり、状態sにおいて行動aを取った後に方策πに
従って行動し続けたときの期待される報酬の総和を表します。
ベルマン方程式は、各行動の価値を方策に従う確率で重み付けし、その合計を取ることで状態の価値を算出します。これにより、エージェントが長期的にどの程度の報酬を得られるかを評価できるようになります。
次に、マルコフ決定過程では、状況sにおいてどの行動aを取るかが重要であり、それを表す方策π(a∣s)があります。方策勾配法では、この方策を最適化することにより、最終的には最も良い結果(報酬)をもたらす行動を選ぶようにします。
方策勾配法の目的は、期待される報酬を最大化する方策を見つけることです。これは、報酬の期待値を最大にする方策のパラメータθを見つけることに他なりません。期待される報酬の期待値は、J(θ)として表され、価値関数Vπ(s)や行動価値関数Qπ(s,a)を使って計算されます。J(θ)は、方策πに依存し、方策がパラメータθによって定義されるため、方策のパラメータを変更することで最大化を図ります。
ベルマン方程式は、状態価値や行動価値を再帰的に定義し、価値ベースの強化学習アルゴリズムで価値関数を更新する際に使用されます。方策勾配法では直接使われることはありませんが、ベルマン方程式はActor-Criticアルゴリズムで使われる「クリティック」による価値関数の更新において中心的な役割を果たします。
方策勾配法は、方策のパラメーターを直接調整することで、期待される報酬を最大化しようとするアプローチです。REINFORCEアルゴリズムは方策勾配法の一種で、実際に取った行動の結果(報酬)に基づいて、方策のパラメーターを更新します。
REINFORCEアルゴリズムでは、方策勾配の分散を減らすためにベースラインb(s)を導入します。これは通常、その状態の価値Vπ(s)として選ばれ、行動価値Qπ(s,a)から引かれます。これにより、期待報酬以上の行動は強化され(ポジティブな勾配)、期待報酬以下の行動は弱化されます(ネガティブな勾配)。
A3C: Actor-Criticアルゴリズムの一種で、Actor(方策)とCritic(価値関数)の両方を学習します。Actorは方策を提案し、Criticは提案された方策の良さを評価します。
Actor(方策) 行動の選択
Actorは各時刻tにおける行動atを確率的方策π(s,a)= p(s|a;w)に従って生成
Critic(価値関数) 行動の評価
criticが状態価値V(s)= E[Rt|st=s]を学習することで将来の報酬を予測し,より価値の高い状態へ遷移するような行動を強化するようにactorに強化信号を送る.
方策勾配法系の様々なアルゴリズム
方策勾配法は、強化学習の一種で、エージェントの行動方策(Policy)を直接的に最適化する手法です。ここでいう「方策」とは、特定の状態でどの行動を取るべきかを定めたルールのことです。方策勾配法では、期待される報酬(期待収益)を最大化する方向に方策のパラメータを更新していきます。
方策勾配法系(非Actor-Critic)
方策勾配法は、期待収益を最大化することを目的にしています。具体的には、方策関数をパラメータ θ で表し、そのパラメータを調整することによって、より多くの報酬を得られる行動が選択されやすくなるように学習を進めます。学習が進むにつれて、エージェントは有利な行動を取る傾向が強くなります。
'Vanilla' Policy Gradient
'Vanilla' Policy Gradientは方策勾配法の基本形で、複雑な行動空間に対しても比較的単純な方法で方策を最適化します。この手法では、得られた報酬の合計を使って期待収益を近似し、方策のパラメータを更新します。しかし、報酬の合計だけを使うと分散が大きくなるため、ベースラインという値を使って分散を減らすテクニックを用います。
REINFORCE
REINFORCEアルゴリズムは、複数のエピソードを通じて得られた報酬の平均を使って、期待収益を近似します。ベースラインとしては報酬の平均が用いられることが多く、個々のエピソードで得られた報酬をもとにパラメータを更新していきます。REINFORCEは、期待収益を直接的に最大化するためのシンプルで効果的な手法であり、AlphaGoのような複雑な問題に対する強化学習アルゴリズムにも利用されています。
方策勾配法では、エージェントがより良い行動を学習するために期待収益を最大化する方向にパラメータを更新します。'Vanilla' Policy GradientとREINFORCEは、方策勾配法の中でも特に基本的なアルゴリズムで、エージェントが最適な行動を見つけるための学習過程を単純化し、高い効果を得ることができます。これらの手法はシンプルでありながら、強化学習における複雑なタスクを解決する強力なツールとなっています。
3. 両方を組み合わせたアプローチ
最後に、価値または行動価値と方策の両方を学習するアプローチがあります。A3C(Asynchronous Advantage Actor-Critic)、A2C(Advantage Actor-Critic)、AlphaGOがこのカテゴリに含まれます。これらの方法は、方策と価値の両方を組み合わせることで、学習プロセスを改善しようと試みます。
A3C の概要は以下になります
A3C: Actor-Criticアルゴリズムの一種で、Actor(方策)とCritic(価値関数)の両方を学習します。Actorは方策を提案し、Criticは提案された方策の良さを評価します。
Actor-Criticアルゴリズム
Actor(方策) 行動の選択
Actorは各時刻tにおける行動atを確率的方策π(s,a)= p(s|a;w)に従って生成
Critic(価値関数) 行動の評価
criticが状態価値V(s)= E[Rt|st=s]を学習することで将来の報酬を予測し,より価値の高い状態へ遷移するような行動を強化するようにactorに強化信号を送る.
Actor
Actorはエージェントがどの行動をとるかを決定します。これは確率的方策としてモデル化され、パラメータ w によってその振る舞いが決定されます。Actorの目的は、将来得られる報酬の期待値を最大化することです。報酬 Rt は時間 t における即時報酬 rt の総和で、割引率 γ を使って将来の報酬よりも現在の報酬を重視するように計算されます。
Critic
Criticは現在の状態の価値 V(s) を評価します。これは将来得られる報酬 Rt の予測であり、TD(Temporal Difference)学習などの方法を用いて更新されます。Criticが学習することで、より価値の高い行動をActorに推奨することができます。
Actorの更新
Actorのパラメータ wt の更新は、目的関数 E(wt) を増加させるように行われます。ただし、E(w) を直接計算することはできないため、Criticからの評価を基にして更新されます。
数式の説明
方策パラメータ w に対する目的関数の勾配に関する表現です。勾配を使ってパラメータを更新することで、期待される報酬 E(w) を増やすことができます。
更新規則の期待値が状態価値関数 V に依存しないことを示しています。これは、Actorが最適な方策を獲得するために、Criticの価値関数が完全でなくても学習が進むことを意味します。
Actor-Critic法 まとめ
Actor-Critic法では、Actorが行動を選択し、Criticがその行動の良さを評価します。ActorはCriticの評価に基づいて行動方策を更新し、最終的には最適な方策を獲得することを目指します。TD学習を用いたCriticの評価は不完全でも、Actorは有効な学習を進めることができます。アルゴリズムは、Actorの行動選択とCriticの価値評価の間でフィードバックループを形成し、エージェントがより良い戦略を学習することを助けます。
Actor-Criticに基ずく様々なアルゴリズム
Actor-Critic系のアルゴリズムは、方策(Policy)と価値(Value)の両方を利用して学習を行う強化学習の手法です。この系統のアルゴリズムは「Actor」が行動を決定し、「Critic」がその行動の価値を評価するという役割分担が特徴です。
Actor-Critic系
Actor-Critic: Actorは行動を決定し、Criticはその行動の価値を評価します。Criticの評価に基づいてActorは行動方策を更新するため、学習が安定して速く進むとされています。
Actor(方策): "Actor"は、どの行動を取るかを決定する方策そのものです。方策πθ(a∣s)は、状態sにおいて行動aを選ぶ確率を与えます。この方策は、パラメータθによって調整され、勾配上昇法によって期待報酬を最大化する方向にパラメータが更新されます。
Critic(価値関数): "Critic"は、取られた行動がどれだけ良いかを評価する価値関数です。REINFORCEアルゴリズムでは行動価値関数Q(s,a)を直接推定することはありませんが、Actor-Criticアルゴリズムでは、Criticが行動価値関数Q(s,a)や状態価値関数V(s)を推定します。Criticによる推定値は、Actorが方策のパラメータをより効果的に更新するための基準となります。
Actor-Criticモデルでは、"Actor"が行動を決定し、"Critic"がその行動の良し悪しを評価します。Criticからのフィードバックにより、Actorはより良い方策を学習するために自身のパラメータを更新していくという構造になっています。
この相互作用により、方策はより効果的に最適化され、強化学習エージェントのパフォーマンスが向上します。Criticがいない場合(例えばREINFORCEアルゴリズムのように)、方策の更新は不安定になりがちで、より多くのサンプルを必要としますが、Criticの存在により、より効率的で安定した学習が可能になります。
A3C (Asynchronous Advantage Actor-Critic)
A3C: 複数のエージェントが非同期で学習を行い、それぞれが異なる環境の経験から学びます。ベースラインとしては状態価値関数を使用し、エントロピー項を加えることで探索を促進します。分散処理を利用することで学習速度を向上させています。
エージェントが過去にとった行動が期待していたよりも良かったのか、悪かったのかを評価し、その情報を使って未来においてより良い行動を選択するために、方策のパラメータをどのように調整すべきかを教えてくれる
DDPG (Deep Deterministic Policy Gradient)
DDPG: 決定論的な方策を用い、連続的な行動空間において効率的に学習を行うことができます。DQNの手法を取り入れた価値関数の学習と組み合わせています。
TRPO (Trust Region Policy Optimization)
TRPO: 方策の更新時に信頼領域を設定し、大きな更新によるパフォーマンスの劣化を防ぎます。KLダイバージェンスを用いた制約が特徴です。
PPO (Proximal Policy Optimization)
PPO: TRPOのアイデアをさらに発展させ、計算効率を上げたアルゴリズムです。目的関数の変動をクリップすることで安定した学習を実現します。
ACER (Actor Critic with Experience Replay)
ACER: Actor-Critic法に経験再生を組み合わせたアルゴリズムで、より効率的な学習が可能です。
UNREAL (Unsupervised Reinforcement and Auxiliary Learning)
UNREAL: 補助タスクを取り入れたA3Cの拡張版で、学習プロセスをさらに強化します。
NAC (Natural Actor-Critic)
NAC: 自然勾配を用いたActor-Criticアルゴリズムで、方策の更新をより効率的に行います。
これらのアルゴリズムは、ActorとCriticの相互作用を通じて、エージェントが環境内で最適な行動を学習するように設計されています。それぞれに特徴的なテクニックや改善点があり、特定の問題に対して適切な手法を選択することが重要です。Actor-Critic系のアルゴリズムは、学習の安定性と効率性を高めるために様々なアプローチが試されており、強化学習の分野で広く研究されています。
様々なアルゴリズムの一覧は以下のサイトで様々な種類を確認できます
この記事が気に入ったらサポートをしてみませんか?
